Algorytmy podzielności przez 7

Zapewne każdy Czytelnik Delty wie, jak sprawdzić, czy nawet duża liczba jest podzielna przez 3, czy przez 8. Metody tego typu wprowadzane są już w młodszych klasach szkoły podstawowej, dzięki czemu są powszechnie znane. Jednak tytułowy problem podzielności akurat przez 7 jest w typowym kursie szkolnym pomijany. W niniejszym artykule postanowiliśmy więc tę lukę uzupełnić i przedstawić przegląd różnych metod na sprawdzenie podzielności przez 7.

A więc do dzieła:

Metoda: pomnóż przez 2 i odejmij

Pojedynczy krok algorytmu jest następujący: jeśli liczba 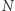$N$ jest co najmniej trzycyfrowa, to zastępujemy ("nadpisujemy") ją liczbą:

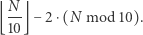N mod10). ⌊--⌋− 2 ⋅(N 10

Gdy zmienna 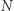$N$ stanie się dwucyfrowa, to po prostu sprawdzamy jej podzielność przez 7 wprost. Pozostawiamy Czytelnikom udowodnienie poprawności tej metody. Od strony złożoności algorytmicznej - dostajemy liniowy koszt zarówno czasowy, jak i pamięciowy.

Metoda kolejnych trójek

Skorzystamy tutaj z kongruencji 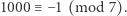$1000 ≡− 1 (mod 7).$

Przyjmujemy, że liczba cyfr liczby 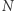$N$ jest podzielna przez 3, w przeciwnym razie najbardziej znaczące miejsca możemy uzupełnić zerami.

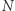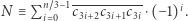Możemy zatem zapisać $|N$ jako $n~3−1----------- i |Pi 0 c3i+2c3i+1c3i⋅1000 .$ Stąd, i z powyższej kongruencji, mamy $≡Pn~3−1i0c3i+2c3i+1c3i⋅(−1)i. |N$ Metoda sprawdzenia podzielności sprowadza się więc do arytmetyki liczb trzycyfrowych. Dla przykładu liczba 5 242 636 881 jest podzielna przez 7, bo 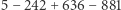$|5− 242 +636 − 881$ jest podzielna przez 7.

Metoda potęgowania trójki

Kolejny sposób bazuje na poniższej obserwacji:

Niech

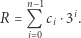n−1 R = Q c ⋅3i. i 0 i

(*)

Wówczas 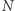$|N$ jest podzielna przez 7 wtedy i tylko wtedy, gdy 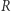$R$ jest podzielna przez 7.

Powyższe stwierdzenie wynika wprost z faktu, że dla każdego całkowitego 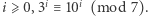$|i⩾ 0,3i≡ 10i (mod 7).$

Potęgowanie jest dość czasochłonne, ale ponieważ interesuje nas tylko reszta z dzielenia, więc możemy odpowiednie potęgi 3 zastąpić odpowiednim wynikiem modulo 7:

$pict$

(Kolejne reszty pojawiają się cyklicznie w cyklu długości 6.)

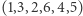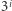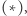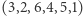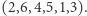Możemy zatem zapamiętać permutację $(1,3,2,6,4,5)$ i podstawiać cyklicznie jej elementy w miejsce kolejnego mnożnika $i 3$ we wzorze $|(∗),$ i na końcu sprawdzić, czy otrzymana liczba dzieli się przez 7. Co ciekawe, każde przesunięcie cyklu również poprawnie rozstrzygnie podzielność przez 7, tj. możemy mnożyć kolejne cyfry przez np. $|(3,2,6,4,5,1)$ czy $(2,6,4,5,1,3).$ Ta ważna własność - która będzie kluczowa również w rozumowaniu pod koniec tego tekstu - wynika z tego, że dla dowolnego naturalnego 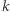$|k$ liczba 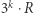$3k⋅R$ jest podzielna przez 7 wtedy i tylko wtedy, gdy 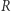$|R$ jest podzielna przez 7, ponieważ liczby 3 oraz 7 są względnie pierwsze.

Mamy zatem 6 różnych permutacji, które można zastosować równoważnie w algorytmie. Dla przykładu, żeby sprawdzić, czy liczba 12 345 678 jest podzielna przez 7, możemy sprawdzić sumę (wybraliśmy cykl 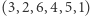$|(3,2,6,4,5,1)$ ):

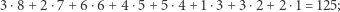3⋅8+ 2 ⋅7+ 6 ⋅6 + 4⋅5 + 5⋅4 +1 ⋅3+ 3⋅2 + 2⋅1 = 125;

następnie 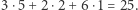$|3⋅5 +2 ⋅2+ 6 ⋅1 = 25.$ Ostatnia suma nie jest podzielna przez 7, zatem wyjściowa liczba też nie jest podzielna przez 7. Natomiast 12 345 683 jest podzielna przez 7, gdyż odpowiednia suma cyfr po analogicznym podstawieniu wynosi 112, a ta jest podzielna przez 7.

Zauważmy też, że permutację 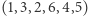$|(1,3,2,6, 4,5)$ możemy zapisać równoważnie jako 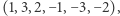$(1,3,2,−1,−3,−2),$ co istotnie może ułatwić zapamiętanie metody (de facto pamiętamy cykl tylko trzech liczb i pilnujemy zmiany znaku po każdym obrocie).

Jeśli metodę implementujemy na komputerze i chcemy naprawdę efektywnie to zrobić, jeszcze lepiej zapisać cykl jako 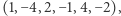$(1,− 4,2,−1,4,−2),$ gdyż mnożenie przez małe potęgi 2 jest dla komputera wyjątkowo naturalne (ten i następny wariant algorytmu nie był znany autorowi tekstu wcześniej).

Zauważmy, że powyższa metoda może działać w stałej pamięci, jeśli liczba jest podawana na wejściu "strumieniowo" (cyfra po cyfrze) od najmniej znaczącej cyfry.

A co, gdy liczba jest podawana na wejściu od cyfry najbardziej znaczącej?

Tutaj też poradzimy sobie w stałej pamięci. Wystarczy tylko pewien cykl odwrócić (np. przyjąć 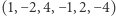$| (1,−2,4,− 1,2,−4)$ ) oraz postępować dalej podobnie jak w klasycznym algorytmie - łatwo sprawdzić, że wówczas obliczymy tę samą sumę, co w standardowej procedurze (choć, co ciekawe: dla pewnego - nieznanego z góry - spośród sześciu poprawnych cykli)!