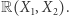Sumy kwadratów wielomianów
Suma kwadratów najczęściej kojarzy się nam z twierdzeniem Pitagorasa - słusznie, ale warto wiedzieć, że temat ten ma swoje miejsce również w teorii liczb, gdzie interesuje nas, czy daną liczbę całkowitą można przedstawić w postaci sumy kwadratów innych liczb całkowitych. Intrygujące jest również pytanie, ile składników znajduje się w tej sumie. Osiągnięcia w tym zakresie mieli między innymi Fermat, Euler i Lagrange...
Fermat wysnuł hipotezę, że każda liczba pierwsza postaci 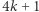 jest sumą dwóch kwadratów, co udowodnił Euler. Istnieje twierdzenie, które podaje, jakie warunki musi spełniać liczba naturalna, aby była sumą dwóch kwadratów.
jest sumą dwóch kwadratów, co udowodnił Euler. Istnieje twierdzenie, które podaje, jakie warunki musi spełniać liczba naturalna, aby była sumą dwóch kwadratów.
Twierdzenie 1. Liczbę naturalną można przedstawić w postaci sumy dwóch kwadratów wtedy i tylko wtedy, gdy każdy jej czynnik pierwszy postaci 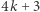 występuje w parzystej potędze.
występuje w parzystej potędze.
Przykłady:
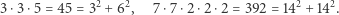 |
Niektóre liczby wymagają trzech kwadratów:
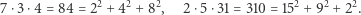 |
A gdybyśmy chcieli przedstawić dowolną liczbę naturalną jako sumę kwadratów? Czy da się to zrobić dla każdej liczby naturalnej? I czy możemy oszacować liczbę składników w takiej sumie? Okazuje się, że bez zakładania dodatkowych warunków trzy kwadraty to również za mało. W 1770 roku Lagrange udowodnił następujące
Twierdzenie 2 (Lagrange, 1770). Każda liczba naturalna da się przedstawić w postaci sumy czterech kwadratów liczb naturalnych.
Oczywiście, twierdzenie Lagrange'a można zmodyfikować na różne sposoby, na przykład zmieniając postać składników. Istnieją odpowiednie twierdzenia związane z przedstawieniem liczby naturalnej jako sumy sześcianów. Jest również teoria związana z twierdzeniem Waringa, w którym pytamy o najmniejszą potrzebną liczbę składników w sumie 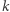 -tych potęg, aby móc otrzymać w wyniku dowolną liczbę naturalną. Jednak w naszych dociekaniach zostaniemy przy kwadratach. Jeżeli chodzi o przedstawienie liczby naturalnej jako sumy kwadratów, to właściwie twierdzenie Lagrange'a wyczerpuje temat.
-tych potęg, aby móc otrzymać w wyniku dowolną liczbę naturalną. Jednak w naszych dociekaniach zostaniemy przy kwadratach. Jeżeli chodzi o przedstawienie liczby naturalnej jako sumy kwadratów, to właściwie twierdzenie Lagrange'a wyczerpuje temat.
Wątek teorii liczb jest tylko wstępem do rozważań nieco innych. Kto powiedział, że sumy kwadratów możemy rozpatrywać tylko w kontekście liczb? Dlaczego zamiast nich nie możemy wziąć pod uwagę innych obiektów matematycznych - na przykład wielomianów? Problemem przedstawienia wielomianu jako sumy kwadratów innych wielomianów jako pierwszy zajął się David Hilbert. Sformułował on następujące
Pytanie. Czy z nieujemnej określoności wielomianu wynika to, że możemy przedstawić go jako sumę kwadratów wielomianów?
Rozważmy proste wersje tego problemu. Weźmy pod lupę najpierw wielomiany jednej zmiennej o współczynnikach rzeczywistych, których zbiór oznaczymy przez ![R[X].](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/1x-b377ea6706249bac84dfb7159c56379b3b5a182a-im-33,33,33-FF,FF,FF.gif)
Dowód. Załóżmy, że ![W ∈R[X]](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/1x-7cc85dd6b005af9b8a45e13bdb8d97b88237c78d-im-33,33,33-FF,FF,FF.gif) jest nieujemnie określony. Z Zasadniczego Twierdzenia Algebry wynika, że każdy wielomian o współczynnikach rzeczywistych jest iloczynem wielomianów rzeczywistych pierwszego i drugiego stopnia. Ponieważ
jest nieujemnie określony. Z Zasadniczego Twierdzenia Algebry wynika, że każdy wielomian o współczynnikach rzeczywistych jest iloczynem wielomianów rzeczywistych pierwszego i drugiego stopnia. Ponieważ 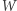 jest nieujemnie określony, więc można go przedstawić jako iloczyn nieujemnie określonych wielomianów drugiego stopnia (Czytelniku, dlaczego?). Można go zatem zapisać w postaci
jest nieujemnie określony, więc można go przedstawić jako iloczyn nieujemnie określonych wielomianów drugiego stopnia (Czytelniku, dlaczego?). Można go zatem zapisać w postaci

gdzie 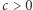 oraz wyróżnik każdego kwadratowego czynnika jest niedodatni. Wykorzystując przedstawienie trójmianu kwadratowego w postaci kanonicznej, dostajemy
oraz wyróżnik każdego kwadratowego czynnika jest niedodatni. Wykorzystując przedstawienie trójmianu kwadratowego w postaci kanonicznej, dostajemy

Stąd

gdzie ![p1,...,pn ∈R[X].](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/7x-7cc85dd6b005af9b8a45e13bdb8d97b88237c78d-im-33,33,33-FF,FF,FF.gif) Dalej korzystamy z tożsamości
Dalej korzystamy z tożsamości

Następnie przekształcamy nasz iloczyn zgodnie z powyższą równością, aż będzie on równy sumie kwadratów pewnych wielomianów ![| W1,W2 ∈R[X].](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/9x-7cc85dd6b005af9b8a45e13bdb8d97b88237c78d-im-33,33,33-FF,FF,FF.gif)
Naturalnie, pojawia się pytanie, czy analogiczne twierdzenie zachodzi dla wielomianów dwóch zmiennych o współczynnikach rzeczywistych (których zbiór oznaczać będziemy przez ![R[X1,X2]](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/1x-b57ca85b404199e1a30da4c927433e1eb4b9de14-im-33,33,33-FF,FF,FF.gif) ). Okazuje się, że nie, a chcąc udowodnić ten fakt, można posłużyć się kontrprzykładem. Wielomian
). Okazuje się, że nie, a chcąc udowodnić ten fakt, można posłużyć się kontrprzykładem. Wielomian
![2 2 2 4 4 2 W (X1,X2) = 1− 3X1X2 +X1X2 + X1X2∈ R[X1,X2],](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/2x-b57ca85b404199e1a30da4c927433e1eb4b9de14-dm-33,33,33-FF,FF,FF.gif)
nazywany wielomianem Motzkina, był pierwszym przykładem dodatnio określonego wielomianu, który nie jest sumą kwadratów innych wielomianów. Pojawił się stosunkowo późno, bo dopiero w 1967 roku. Jego dodatnia określoność jest konsekwencją nierówności pomiędzy średnimi - średnią arytmetyczną i średnią geometryczną. Mamy

Podstawiając 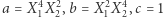 otrzymujemy
otrzymujemy

Wykażemy teraz, że 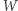 nie jest sumą kwadratów wielomianów. Dla dowodu nie wprost załóżmy, że
nie jest sumą kwadratów wielomianów. Dla dowodu nie wprost załóżmy, że 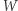 jest sumą pewnych
jest sumą pewnych 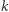 kwadratów, czyli
kwadratów, czyli
![k W = Q W2, Wi∈ R[X1,X2]. i 1 i](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/9x-b57ca85b404199e1a30da4c927433e1eb4b9de14-dm-33,33,33-FF,FF,FF.gif)
Z tej racji, że stopień wielomianu 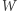 jest równy
jest równy 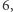 to stopień każdego z wielomianów
to stopień każdego z wielomianów 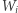 jest równy co najwyżej
jest równy co najwyżej 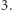 Stąd każdy wielomian
Stąd każdy wielomian 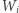 składa się z wielomianów
składa się z wielomianów

z pewnymi rzeczywistymi współczynnikami. Zauważmy, że 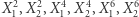 nie występują w jawnej postaci wielomianu
nie występują w jawnej postaci wielomianu 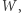 więc składniki
więc składniki 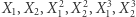 nie mogą występować w żadnym z
nie mogą występować w żadnym z 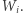 Stąd
Stąd

dla pewnych liczb rzeczywistych 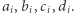 Wtedy jednak
Wtedy jednak 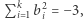 co daje sprzeczność; wielomianu Motzkina nie można zatem przedstawić w postaci sumy kwadratów wielomianów dwóch zmiennych.
co daje sprzeczność; wielomianu Motzkina nie można zatem przedstawić w postaci sumy kwadratów wielomianów dwóch zmiennych.
Widzimy więc, że odpowiedź na pytanie Hilberta jest negatywna, choć są również "częściowo pozytywne" wyniki, jak poniższy:
Twierdzenie 4 (Hilbert, 1888). Niech ![W ∈ R[X1,X2]](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/1x-63b54fafaac55fa6977a6e0435e3fbea27bd5cf7-im-33,33,33-FF,FF,FF.gif) będzie nieujemnie określonym wielomianem stopnia
będzie nieujemnie określonym wielomianem stopnia 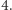 Wtedy
Wtedy 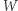 jest sumą trzech kwadratów z
jest sumą trzech kwadratów z ![R[X ,X]. 1 2](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/4x-63b54fafaac55fa6977a6e0435e3fbea27bd5cf7-im-33,33,33-FF,FF,FF.gif)
Skoro nie każdy nieujemnie określony wielomian możemy zapisać jako sumę kwadratów innych wielomianów, spróbujmy poszerzyć zakres naszych poszukiwań - zamiast wielomianów zapytajmy o ilorazy wielomianów, czyli tak zwane funkcje wymierne. W pewnym sensie są one dla wielomianów tym samym, czym liczby wymierne dla liczb całkowitych. Zbiór funkcji wymiernych  zmiennych oznaczać będziemy przez
zmiennych oznaczać będziemy przez 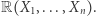 W tym kontekście odpowiedzi na nasze pytania dostarcza poniższe
W tym kontekście odpowiedzi na nasze pytania dostarcza poniższe
Twierdzenie 5 (Artin, 1927). Niech wielomian 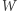 będzie nieujemnie określony. Wtedy
będzie nieujemnie określony. Wtedy 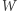 jest sumą kwadratów z
jest sumą kwadratów z 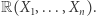
Po opublikowaniu wyniku Artina pojawiły się inne pytania. Jak dużo kwadratów jest w rozkładzie na sumę? Jeden z wyników w tym zakresie należy do Hilberta.
Twierdzenie 6 (Hilbert, 1893). Niech wielomian ![|W ∈R[X ,X ] 1 2](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/1x-37a6b879b738ccc4d35e1627e11d3b029bf99820-im-33,33,33-FF,FF,FF.gif) będzie nieujemnie określony. Wtedy
będzie nieujemnie określony. Wtedy 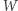 jest sumą czterech kwadratów z
jest sumą czterech kwadratów z 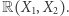
Naturalne jest pytanie, czy możemy wzmocnić to twierdzenie przez zapisanie dodatnio określonego wielomianu jako sumy trzech kwadratów funkcji wymiernych. Odpowiedź jest negatywna i z pomocą jako kontrprzykład ponownie przychodzi nam wielomian Motzkina - tym razem jednak uzasadnienie nie jest elementarne i korzysta z dziedziny zwanej geometrią algebraiczną.
Okazuje się, że wielomian Motzkina nie jest w tym sensie wyjątkowy. Jean-Louis Colliot-Thélène pokazał w 1993 roku, że w zbiorze wielomianów stopnia co najmniej 6 te, które można przedstawić w postaci sumy trzech kwadratów funkcji wymiernych, stanowią pomijalny zbiór zarówno z topologicznego, jak i teoriomiarowego punktu widzenia; szczegóły można znaleźć na przykład w artykule Oliviera Benoista: Writing Positive Polynomials as Sums of (Few) Squares.
Teraz wróćmy do liczby składników w przypadku dowolnej liczby zmiennych. O tym, jak można ją oszacować dla funkcji wymiernych 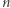 zmiennych, mówi poniższe twierdzenie Pfistera.
zmiennych, mówi poniższe twierdzenie Pfistera.
Twierdzenie 8 (Pfister, 1967). Niech wielomian ![W ∈ R[X ,...,X ] 1 n](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/2x-912be1a88cdd30921c9421fb52fcbd4e4967282e-im-33,33,33-FF,FF,FF.gif) będzie nieujemnie określony. Wtedy
będzie nieujemnie określony. Wtedy 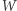 jest sumą
jest sumą 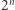 kwadratów z
kwadratów z 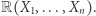
Nasuwa się kolejne pytanie: czy ograniczenie 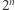 może zostać poprawione? Innymi słowy, czy istnieje nieujemnie określony wielomian z
może zostać poprawione? Innymi słowy, czy istnieje nieujemnie określony wielomian z ![R[X1,...,Xn],](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/2x-7545aa626e35bf8d322536b95b58164ef7877e1c-im-33,33,33-FF,FF,FF.gif) który nie jest sumą
który nie jest sumą 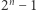 kwadratów z
kwadratów z 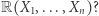 Dylemat ten został sformułowany przez Albrechta Pfistera zaraz po opublikowaniu dowodu, że liczba składników
Dylemat ten został sformułowany przez Albrechta Pfistera zaraz po opublikowaniu dowodu, że liczba składników 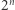 jest wystarczająca. Na chwilę obecną wiadomo jedynie, że
jest wystarczająca. Na chwilę obecną wiadomo jedynie, że 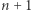 to za mało. Jak widać, choć siedemnasty problem Hilberta został rozwiązany już w
to za mało. Jak widać, choć siedemnasty problem Hilberta został rozwiązany już w  roku, to temat związany z tym zagadnieniem jest pełen kwestii nierozstrzygniętych. Do zrobienia wciąż pozostaje wiele, a zaprezentowane tutaj twierdzenia są tylko częścią większej układanki.
roku, to temat związany z tym zagadnieniem jest pełen kwestii nierozstrzygniętych. Do zrobienia wciąż pozostaje wiele, a zaprezentowane tutaj twierdzenia są tylko częścią większej układanki.
![W ∈R[X]](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/2x-b377ea6706249bac84dfb7159c56379b3b5a182a-im-33,33,33-FF,FF,FF.gif)
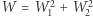
![W1,W2 ∈R[X].](/math/temat/matematyka/teoria_liczb/2019/02/26/Sumy_kwadratow_wielomianow/4x-b377ea6706249bac84dfb7159c56379b3b5a182a-im-33,33,33-FF,FF,FF.gif)