Porównywanie wież potęgowych
Zadanie. Używając dowolnych cyfr oraz operacji 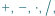 potęgowania i nawiasów, należy zapisać działanie o możliwie największym wyniku. Czas na zapisanie działania to 10 sekund.
potęgowania i nawiasów, należy zapisać działanie o możliwie największym wyniku. Czas na zapisanie działania to 10 sekund.

Drogi Czytelniku, z dużym prawdopodobieństwem zapisałeś coś takiego 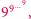 czyli wieżę potęgową. Działanie
czyli wieżę potęgową. Działanie 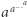 oznaczmy przez
oznaczmy przez 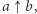 gdzie
gdzie 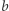 oznacza, ile razy liczba
oznacza, ile razy liczba 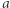 pojawia się w wieży. Możemy rozważyć również wieże, w których kolejne "piętra" nie są taką samą liczbą. Wprowadźmy następującą notację:
pojawia się w wieży. Możemy rozważyć również wieże, w których kolejne "piętra" nie są taką samą liczbą. Wprowadźmy następującą notację:
![a:::an a12 = [a1;a2;...;an].](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/6x-7f1751380f5e37ec4bf4eca05f94549cbadf0141-dm-33,33,33-FF,FF,FF.gif)
Przyjmijmy, że wszystkie liczby w wieży, poza ostatnią, muszą być całkowite i niezerowe. Wartość  nazywamy wysokością wieży. Ponadto zastosujemy następujące uproszczenie: jeżeli liczba
nazywamy wysokością wieży. Ponadto zastosujemy następujące uproszczenie: jeżeli liczba  pojawia się w wieży
pojawia się w wieży 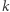 razy pod rząd, to będziemy to oznaczać przez
razy pod rząd, to będziemy to oznaczać przez 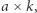 na przykład:
na przykład:
![5 3333 = 3 4 = [3;3;3;3] = [3× 4], 3555 = [3;5 ×4].](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/5x-eb03de9a49a987e36dcc3ce618315d89d4bb0121-dm-33,33,33-FF,FF,FF.gif)
W tym artykule zajmiemy się takimi właśnie wieżami. Dokładniej, jak już mógł zdradzić tytuł, będziemy starali się wskazać sposób porównywania wież.
Zaczniemy od znalezienia ogólnego sposobu na zapisanie wyrażenia ![|[a ;a ;...;a ] 1 2 n](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/1x-7803bbafaeb112fba39681a5e6a1239dcdf73d7c-im-33,33,33-FF,FF,FF.gif) za pomocą wieży
za pomocą wieży ![[10 ×k; y],](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/2x-7803bbafaeb112fba39681a5e6a1239dcdf73d7c-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie 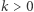 jest naturalne, a
jest naturalne, a 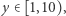 czyli
czyli
![[a1;a2;...;an] = [10× k;y].](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/5x-7803bbafaeb112fba39681a5e6a1239dcdf73d7c-dm-33,33,33-FF,FF,FF.gif)
Przy tym staramy się znaleźć takie 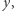 żeby nie zmieniać wartości wieży, albo (co częstsze) zmienić ją możliwie nieznacznie. Wieżę
żeby nie zmieniać wartości wieży, albo (co częstsze) zmienić ją możliwie nieznacznie. Wieżę ![|[10 × k;y]](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/7x-7803bbafaeb112fba39681a5e6a1239dcdf73d7c-im-33,33,33-FF,FF,FF.gif) nazwiemy znormalizowaną. Sprowadzanie dwóch wież do takiej postaci pozwala sprawnie porównać ich wartości - wystarczy porównać wysokości wież znormalizowanych oraz, jeśli wysokości są identyczne, ostatnią liczbę w wieży. Na kilku przykładach zaprezentujemy normalizację.
nazwiemy znormalizowaną. Sprowadzanie dwóch wież do takiej postaci pozwala sprawnie porównać ich wartości - wystarczy porównać wysokości wież znormalizowanych oraz, jeśli wysokości są identyczne, ostatnią liczbę w wieży. Na kilku przykładach zaprezentujemy normalizację.
Przykład 2. Weźmy ![|[9 × 3]](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/1x-c6aaa209f574aa1d1804b1e1c1f97e93913c4339-im-33,33,33-FF,FF,FF.gif) i znajdźmy takie
i znajdźmy takie 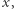 że zachodzi
że zachodzi 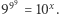 W tym przypadku
W tym przypadku 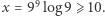 Kolejnym krokiem jest znalezienie takiego
Kolejnym krokiem jest znalezienie takiego 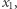 że
że 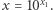 Oczywiście
Oczywiście 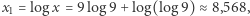 czyli ostatecznie
czyli ostatecznie
![[9× 3] = [10;10;x] ≈ [10;10;8,568]. 1](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/8x-c6aaa209f574aa1d1804b1e1c1f97e93913c4339-dm-33,33,33-FF,FF,FF.gif)

Przykład 3. Rozważmy wreszcie liczbę ![[9× 4]](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/1x-10a1958f512b8efaa2f3edc2e89c3558fefbed63-im-33,33,33-FF,FF,FF.gif) i postąpmy podobnie jak wcześniej. Mamy kolejno:
i postąpmy podobnie jak wcześniej. Mamy kolejno: ![[9 ×4] = 10x,x = [9× 3]log 9,x = 10x1,](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/2x-10a1958f512b8efaa2f3edc2e89c3558fefbed63-im-33,33,33-FF,FF,FF.gif)
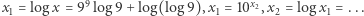 I tu napotykamy kłopot, gdyż liczba
I tu napotykamy kłopot, gdyż liczba 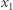 jest sumą dwóch liczb, a nie da się rozbić logarytmu sumy. Zamiast tego spójrzmy na składniki
jest sumą dwóch liczb, a nie da się rozbić logarytmu sumy. Zamiast tego spójrzmy na składniki 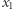 i zauważmy, że zachodzi
i zauważmy, że zachodzi 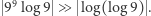 (Obie strony rozważamy w modułach, gdyż liczba
(Obie strony rozważamy w modułach, gdyż liczba 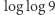 jest ujemna.) Istotnie,
jest ujemna.) Istotnie, 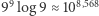 oraz
oraz 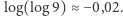 W takim razie zaniedbajmy ten mały składnik. Wtedy
W takim razie zaniedbajmy ten mały składnik. Wtedy 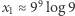 i ostatecznie
i ostatecznie 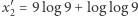 oraz
oraz
![[9 ×4] ≈ [10 × 3;x′] ≈ [10 × 3;8,568]. 2](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/12x-10a1958f512b8efaa2f3edc2e89c3558fefbed63-dm-33,33,33-FF,FF,FF.gif)
Różnica między najwyższymi piętrami, to jest między 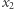 i
i 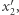 wynosi
wynosi 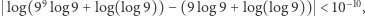 jest więc relatywnie mała.
jest więc relatywnie mała.
Spójrzmy teraz na problem szacowania z nieco innej strony. Najpierw parę narzędzi. Zapiszmy 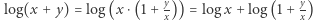 i podstawmy
i podstawmy 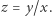 Następnie rozwińmy drugi składnik w szereg Taylora w punkcie
Następnie rozwińmy drugi składnik w szereg Taylora w punkcie 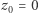

Podstawiając wartości z Przykładu 3., otrzymujemy 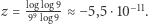 Sprawdźmy, jak wygląda analogiczne przybliżenie dla liczby
Sprawdźmy, jak wygląda analogiczne przybliżenie dla liczby ![[9× 5].](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/6x-e683704ca29b8d503321dda94ec909979281e800-im-33,33,33-FF,FF,FF.gif) W tym przypadku pierwsze przybliżenie stosowane jest do liczb
W tym przypadku pierwsze przybliżenie stosowane jest do liczb ![x = [9× 3]log 9](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/7x-e683704ca29b8d503321dda94ec909979281e800-im-33,33,33-FF,FF,FF.gif) oraz
oraz 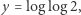 a więc
a więc ![z = yx ≈− [10;− 10;8,568].](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/9x-e683704ca29b8d503321dda94ec909979281e800-im-33,33,33-FF,FF,FF.gif) Ta liczba jest mała, więc możemy dokonać następującego przybliżenia (tylko pierwszy wyraz szeregu Taylora):
Ta liczba jest mała, więc możemy dokonać następującego przybliżenia (tylko pierwszy wyraz szeregu Taylora): 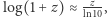 i stwierdzić, że te wartości nie różnią się prawie wcale.
i stwierdzić, że te wartości nie różnią się prawie wcale.
- Cały artykuł dostępny jest w wersji do druku [application/pdf]: (374 KB)
![[9;9]](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/1x-f51d5cae74f7d85e7ae7d28367c4538b0df8ab97-im-33,33,33-FF,FF,FF.gif)
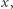
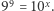
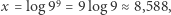
![[9;9] = [10;9log 9]≈ [10;8,588].](/math/temat/matematyka/teoria_liczb/2019/01/29/Porownywanie_wiez_potegowych/5x-f51d5cae74f7d85e7ae7d28367c4538b0df8ab97-dm-33,33,33-FF,FF,FF.gif)
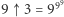 ma w rozwinięciu
ma w rozwinięciu 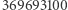 cyfr. Więcej o dużych liczbach i "wykładnikach strzałek" można znaleźć w
cyfr. Więcej o dużych liczbach i "wykładnikach strzałek" można znaleźć w