Jak wyciągnąć  modulo
modulo 
Niech 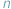 będzie liczbą nieparzystą...
będzie liczbą nieparzystą...
Pytamy, czy istnieje taka liczba całkowita 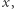 że
że
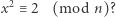 |
(1) |
Jeśli ta kongruencja ma rozwiązanie całkowite 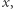 to na pewno istnieje rozwiązanie
to na pewno istnieje rozwiązanie 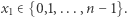 Wtedy liczba
Wtedy liczba 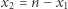 też jest rozwiązaniem. Jak jednak rozstrzygnąć, czy kongruencja (1) w ogóle ma rozwiązania?
też jest rozwiązaniem. Jak jednak rozstrzygnąć, czy kongruencja (1) w ogóle ma rozwiązania?
W przypadku, gdy 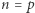 jest liczbą pierwszą, dysponujemy praktycznym algorytmem, który rozstrzyga, czy kongruencja (1) ma rozwiązanie - oparty jest on na tzw. kryterium Eulera. Jest ono ściśle związane z małym twierdzeniem Fermata. To słynne twierdzenie mówi, że jeśli
jest liczbą pierwszą, dysponujemy praktycznym algorytmem, który rozstrzyga, czy kongruencja (1) ma rozwiązanie - oparty jest on na tzw. kryterium Eulera. Jest ono ściśle związane z małym twierdzeniem Fermata. To słynne twierdzenie mówi, że jeśli  nie dzieli się przez liczbę pierwszą
nie dzieli się przez liczbę pierwszą 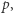 to wówczas
to wówczas

Jeśli kongruencja (1) ma rozwiązanie 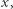 to możemy napisać
to możemy napisać

a zatem ostatecznie
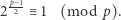 |
(2) |
Kryterium Eulera stanowi, że powyższe rozumowanie można odwrócić: jeśli zachodzi kongruencja (2), to kongruencja (1) ma rozwiązanie. Warto w tym miejscu dodać, że potęgowanie 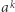 modulo
modulo  łatwo wykonać efektywnie nawet wtedy, gdy liczby
łatwo wykonać efektywnie nawet wtedy, gdy liczby  oraz
oraz 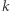 są ogromne! Oto zarys metody. Najpierw zapisujemy wykładnik
są ogromne! Oto zarys metody. Najpierw zapisujemy wykładnik 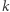 w układzie dwójkowym:
w układzie dwójkowym:

Ponieważ

więc wystarczy wykonać 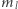 kolejnych podnoszeń do kwadratu, a na koniec
kolejnych podnoszeń do kwadratu, a na koniec 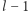 mnożeń - wszystkie operacje wykonujemy modulo
mnożeń - wszystkie operacje wykonujemy modulo 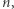 a więc na liczbach mniejszych od
a więc na liczbach mniejszych od 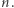
Załóżmy teraz, że liczba 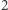 przeszła test Eulera. Nasuwa się teraz pytanie: jak znaleźć
przeszła test Eulera. Nasuwa się teraz pytanie: jak znaleźć  spełniające kongruencję (1)?
spełniające kongruencję (1)?
Jeśli 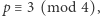 to wystarczy przyjąć
to wystarczy przyjąć

Pokazuje to poniższy rachunek

(na mocy (2)).
Jeżeli natomiast 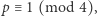 to nieco komplikując powyższą metodę (szczegóły pominiemy), można obliczyć
to nieco komplikując powyższą metodę (szczegóły pominiemy), można obliczyć 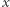 spełniające (1), o ile mamy do dyspozycji taką liczbę
spełniające (1), o ile mamy do dyspozycji taką liczbę 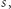 że kongruencja
że kongruencja
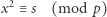 |
(3) |
nie ma rozwiązań. Taką liczbę  nazywamy nieresztą kwadratową modulo
nazywamy nieresztą kwadratową modulo 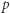 . Łatwo udowodnić, że w ciągu liczb
. Łatwo udowodnić, że w ciągu liczb 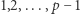 jest dokładnie
jest dokładnie 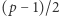 niereszt. Dla pozostałych liczb
niereszt. Dla pozostałych liczb  z powyższego ciągu kongruencja (3) ma rozwiązanie - nazywamy je resztami kwadratowymi modulo
z powyższego ciągu kongruencja (3) ma rozwiązanie - nazywamy je resztami kwadratowymi modulo 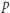 . I tak np. dla
. I tak np. dla 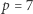 liczby
liczby 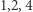 są resztami kwadratowymi, a liczby
są resztami kwadratowymi, a liczby 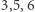 nieresztami kwadratowymi. Natomiast dla
nieresztami kwadratowymi. Natomiast dla 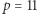 niereszty kwadratowe to
niereszty kwadratowe to 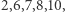 a reszty kwadratowe to
a reszty kwadratowe to 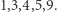 Nieresztę kwadratową
Nieresztę kwadratową 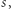 której używamy we wzmiankowanym powyżej algorytmie pierwiastkowania modulo
której używamy we wzmiankowanym powyżej algorytmie pierwiastkowania modulo 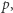 łatwo znaleźć praktycznie nawet dla bardzo dużych liczb pierwszych
łatwo znaleźć praktycznie nawet dla bardzo dużych liczb pierwszych 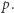 Wystarczy mianowicie wylosować liczbę
Wystarczy mianowicie wylosować liczbę 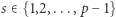 i sprawdzić, czy jest nieresztą kwadratową, stosując, na przykład, kryterium Eulera. W przypadku niepowodzenia losujemy i testujemy inną liczbę
i sprawdzić, czy jest nieresztą kwadratową, stosując, na przykład, kryterium Eulera. W przypadku niepowodzenia losujemy i testujemy inną liczbę  Prawdopodobieństwo wylosowania niereszty w każdej próbie wynosi
Prawdopodobieństwo wylosowania niereszty w każdej próbie wynosi 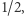 a zatem przeciętnie bardzo szybko znajdziemy nieresztę. Jest to przykład algorytmu zrandomizowanego. Rzucając
a zatem przeciętnie bardzo szybko znajdziemy nieresztę. Jest to przykład algorytmu zrandomizowanego. Rzucając 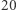 razy symetryczną monetą, możemy, oczywiście, wyrzucić same reszty (niektórzy mówią reszki), ale prawdopodobieństwo tego jest małe.
razy symetryczną monetą, możemy, oczywiście, wyrzucić same reszty (niektórzy mówią reszki), ale prawdopodobieństwo tego jest małe.
A może lepiej testować po kolei liczby 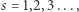 aż do skutku, czyli do napotkania niereszty? Niech więc
aż do skutku, czyli do napotkania niereszty? Niech więc 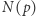 oznacza najmniejszą nieresztę kwadratową modulo
oznacza najmniejszą nieresztę kwadratową modulo 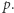 Najlepszy wynik bezwarunkowy pochodzi od D.A. Burgessa
Najlepszy wynik bezwarunkowy pochodzi od D.A. Burgessa

dla każdego 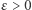 i
i 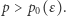 Natomiast przy założeniu uogólnionej hipotezy Riemanna N.C. Ankeny pokazał oszacowanie znacznie lepsze
Natomiast przy założeniu uogólnionej hipotezy Riemanna N.C. Ankeny pokazał oszacowanie znacznie lepsze

Tak więc prymitywny algorytm testowania kolejnych liczb  jest (warunkowo) bardzo efektywny.
jest (warunkowo) bardzo efektywny.
Podsumujmy nasze dotychczasowe rozważania: jeśli moduł  jest liczbą pierwszą, to w zasadzie potrafimy poradzić sobie zarówno z rozstrzygnięciem, czy
jest liczbą pierwszą, to w zasadzie potrafimy poradzić sobie zarówno z rozstrzygnięciem, czy 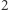 jest resztą kwadratową modulo
jest resztą kwadratową modulo 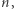 jak i ze znalezieniem wszystkich rozwiązań kongruencji (1) w zbiorze
jak i ze znalezieniem wszystkich rozwiązań kongruencji (1) w zbiorze 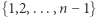 (są dwa takie rozwiązania).
(są dwa takie rozwiązania).
A jak jest dla liczb złożonych 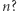 Rozpatrzymy najprostszy przypadek, gdy
Rozpatrzymy najprostszy przypadek, gdy 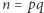 jest iloczynem dwóch różnych liczb pierwszych. Do dzisiaj nie jest znana żadna efektywna uniwersalna metoda rozstrzygania, czy kongruencja (1) ma rozwiązanie. Załóżmy jednak, że dobra wróżka rzekła: Tak, kongruencja
jest iloczynem dwóch różnych liczb pierwszych. Do dzisiaj nie jest znana żadna efektywna uniwersalna metoda rozstrzygania, czy kongruencja (1) ma rozwiązanie. Załóżmy jednak, że dobra wróżka rzekła: Tak, kongruencja 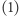 jest rozwiązalna, a Twoje zadanie to znaleźć jej wszystkie rozwiązania
jest rozwiązalna, a Twoje zadanie to znaleźć jej wszystkie rozwiązania 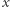 w zbiorze
w zbiorze 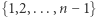 . Załóżmy dalej, że jakimś cudem wypisaliśmy wszystkie (cztery - wynika to z chińskiego twierdzenia o resztach) rozwiązania kongruencji (1):
. Załóżmy dalej, że jakimś cudem wypisaliśmy wszystkie (cztery - wynika to z chińskiego twierdzenia o resztach) rozwiązania kongruencji (1):

Ponieważ kongruencja 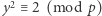 ma dokładnie dwa rozwiązania
ma dokładnie dwa rozwiązania 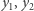 w zbiorze
w zbiorze 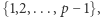 więc dla pewnych
więc dla pewnych 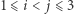 mamy
mamy 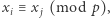 a zatem liczba
a zatem liczba 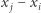 dzieli się przez
dzieli się przez 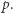 Oczywiście,
Oczywiście, 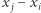 nie dzieli się przez
nie dzieli się przez 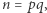 gdyż
gdyż 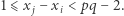 A zatem
A zatem

Liczby NWD 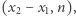 NWD
NWD 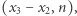 NWD
NWD 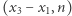 potrafimy obliczyć, bardzo efektywnie stosując najsłynniejszy algorytm na świecie - algorytm Euklidesa. W ten sposób znaleźliśmy nietrywialny dzielnik
potrafimy obliczyć, bardzo efektywnie stosując najsłynniejszy algorytm na świecie - algorytm Euklidesa. W ten sposób znaleźliśmy nietrywialny dzielnik 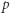 liczby
liczby 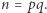 Najbardziej pomógł nam cud (a nie wróżka). Tym samym naszkicowaliśmy główną myśl dowodu twierdzenia, że kompletne rozwiązanie kongruencji (1) dla modułu złożonego
Najbardziej pomógł nam cud (a nie wróżka). Tym samym naszkicowaliśmy główną myśl dowodu twierdzenia, że kompletne rozwiązanie kongruencji (1) dla modułu złożonego  jest co najmniej tak trudne, jak rozkład
jest co najmniej tak trudne, jak rozkład 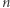 na czynniki pierwsze. Natomiast samo tylko rozstrzygnięcie, czy (1) ma rozwiązanie, wydaje się istotnie łatwiejsze niż rozkład na czynniki, ale jak już wspomnieliśmy wcześniej, nikt nie umie zrobić efektywnie nawet tego.
na czynniki pierwsze. Natomiast samo tylko rozstrzygnięcie, czy (1) ma rozwiązanie, wydaje się istotnie łatwiejsze niż rozkład na czynniki, ale jak już wspomnieliśmy wcześniej, nikt nie umie zrobić efektywnie nawet tego.