O twierdzeniu Słonimskiego

Chaim Zelig Słonimski (1810-1904)
Przy dzieleniu liczb wielocyfrowych metodą pisemną często wykonuje się następującą operację...
Dla takich danych liczb 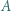 i
i 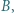 że
że 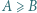 znajdź taką największą cyfrę
znajdź taką największą cyfrę 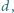 że
że 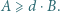
Zwykle wykonujemy tę operację w pamięci nawet dla sporych liczb. Czasem jednak, szczególnie gdy w liczbie 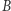 występuje wiele dużych cyfr, nawet wprawny matematyk może się zawahać przy wyborze właściwej cyfry
występuje wiele dużych cyfr, nawet wprawny matematyk może się zawahać przy wyborze właściwej cyfry 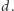 Nie jest to może wielki problem, ale w dawnych czasach, przed upowszechnieniem maszyn liczących, kiedy rachmistrze musieli wykonywać sporo obliczeń na papierze, powodował pewne uciążliwości.
Nie jest to może wielki problem, ale w dawnych czasach, przed upowszechnieniem maszyn liczących, kiedy rachmistrze musieli wykonywać sporo obliczeń na papierze, powodował pewne uciążliwości.
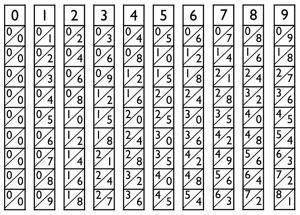
Już w XVII wieku szkocki matematyk John Napier, znany nam dziś głównie jako odkrywca logarytmów, obmyślił bardzo proste urządzenie, które pozwalało szybko obliczać wszystkie wielokrotności podanej liczby wielocyfrowej przy mnożeniu przez pojedyncze cyfry. Z użyciem kości Napiera, bo o nich tu mowa, można bardzo sprawnie wykonać operację opisaną powyżej.
Kości Napiera to podłużne tabliczki, na których wypisano układy liczb. Kości jest 10 rodzajów, po jednym dla każdej cyfry od 0 do 9. Obok wszystkie rodzaje kości.
Każda kość ma w górnym polu wypisaną pojedynczą cyfrę, a poniżej, w 9 kolejnych kwadratach, kolejne wielokrotności tej cyfry zapisane dwiema cyframi rozdzielonymi ukośną linią. W jednym zestawie było zwykle po kilka kości każdego rodzaju.
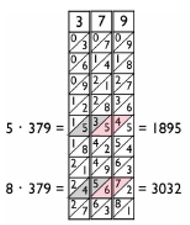
Powiedzmy, że chcemy poznać wynik mnożenia 379 przez 5 i 8. W tym celu układamy obok siebie kości odpowiadające cyfrom 3, 7 i 9 i odczytujemy liczby z piątego i ósmego wiersza, dodając cyfry na ukos jak na rysunku obok.
Mnożąc przez 5, odczytujemy kolejne cyfry wyniku od prawej 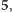
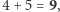
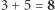 i wreszcie
i wreszcie 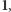 co daje wynik 1895. Czasem w wyniku dodania dwóch cyfr powstaje przeniesienie i wtedy trzeba dodać 1 do sumy cyfr na następnych pozycjach. Przykładowo, mnożąc 379 przez 8, odczytujemy od prawej cyfry
co daje wynik 1895. Czasem w wyniku dodania dwóch cyfr powstaje przeniesienie i wtedy trzeba dodać 1 do sumy cyfr na następnych pozycjach. Przykładowo, mnożąc 379 przez 8, odczytujemy od prawej cyfry 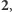
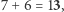
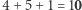 i wreszcie
i wreszcie 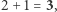 co daje w wyniku 3032.
co daje w wyniku 3032.
Kości Napiera były całkiem przydatne w mnożeniu i dzieleniu liczb wielocyfrowych, szczególnie dla ludzi, którzy mieli problemy z tabliczką mnożenia, co w dawnych czasach było częste nawet wśród nieźle wykształconych osób. Ich stosowanie nadal wymaga jednak wykonywania pewnych (co prawda bardzo prostych) obliczeń w pamięci: dodawania pojedynczych cyfr, a czasem zapamiętywania przeniesienia. W połowie XIX w., kiedy w Europie zaczęły się upowszechniać mechaniczne arytmometry, stało się jasne, że dobrze byłoby udoskonalić kości Napiera tak, aby wyniki mnożenia można było z nich odczytywać całkowicie automatycznie. Autorem jednego z najbardziej pomysłowych urządzeń tego rodzaju był polski wynalazca, dziadek sławnego poety Antoniego Słonimskiego (1895-1976).
Chaim Zelig Słonimski (1810-1904), bo o nim tu mowa, pochodził z ortodoksyjnej rodziny żydowskiej. Młodość spędził na Białostocczyźnie, gdzie odebrał staranne wykształcenie talmudyczne, a jednocześnie samodzielnie studiował matematykę, astronomię i filozofię. Jego życiową misją stało się popularyzowanie nauki w społeczności żydowskiej. Napisał wiele znakomitych książek i artykułów popularnonaukowych w języku hebrajskim, wzbogacając przy tym ten język o wiele terminów technicznych i matematycznych, których w nim wcześniej nie było.
W 1838 r. Słonimski przeniósł się do Warszawy, gdzie poznał Abrahama Sterna, znanego konstruktora maszyn liczących. Wkrótce ożenił się z jego córką Sarą, a po śmierci teścia kontynuował prace nad jego wynalazkami. Zbudował, między innymi, maszynę do mnożenia liczb, opartą na pomysłowej modyfikacji kości Napiera. Zilustrujemy teraz jej działanie na przykładzie. Wypiszmy w tabeli obok rachunki potrzebne do obliczenia kolejnych wielokrotności liczby 379.
W każdym miejscu tabeli znajduje się wyrażenie postaci

gdzie liczby 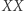 są wielokrotnościami cyfr w pierwszym wierszu i nie zależą od pozostałych cyfr liczby, którą rozważamy. Są to te same liczby, które widnieją na zwykłych kościach Napiera. Cyfra
są wielokrotnościami cyfr w pierwszym wierszu i nie zależą od pozostałych cyfr liczby, którą rozważamy. Są to te same liczby, które widnieją na zwykłych kościach Napiera. Cyfra 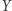 jest równa pierwszej cyfrze liczby
jest równa pierwszej cyfrze liczby 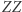 z kolumny po prawej stronie, jak pokazują poziome strzałki. (W ostatniej kolumnie po prawej
z kolumny po prawej stronie, jak pokazują poziome strzałki. (W ostatniej kolumnie po prawej 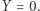 ) Wynik, czyli odpowiednią wielokrotność liczby 379, odczytujemy z drugich cyfr liczb
) Wynik, czyli odpowiednią wielokrotność liczby 379, odczytujemy z drugich cyfr liczb 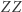 w odpowiednim wierszu. Przykładowo, z zaznaczonych cyfr odczytujemy
w odpowiednim wierszu. Przykładowo, z zaznaczonych cyfr odczytujemy

Popatrzmy teraz na kolumny cyfr 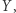 zaznaczone pionowymi strzałkami. Mamy tu, patrząc od prawej, ciągi cyfr:
zaznaczone pionowymi strzałkami. Mamy tu, patrząc od prawej, ciągi cyfr:

Te ciągi pośrednio zależą od wszystkich cyfr na prawo od aktualnej kolumny, a więc potencjalnie trudno przewidzieć, którego z nich trzeba użyć na której pozycji. Ile takich ciągów może się pojawić przy mnożeniu dużych liczb przez pojedyncze cyfry? Można zauważyć, że pierwsza cyfra w takim ciągu musi być równa 0, a każda następna jest równa lub o jeden większa od poprzedniej. Jednak 9-cyfrowych ciągów o tej własności jest aż 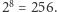 Czy każdy z nich faktycznie może się pojawić?
Czy każdy z nich faktycznie może się pojawić?
Słonimski zauważył (i to właśnie "twierdzenie" jest do dziś opatrzone jego nazwiskiem), że 9-cyfrowych ciągów, które rzeczywiście mogą się pojawić przy obliczaniu wielokrotności liczb wielocyfrowych, jest tylko 28. Dowód tego jest całkiem prosty. Uporządkujmy rosnąco wszystkie nieskracalne ułamki zwykłe między 0 a 1, o mianowniku nie większym niż 9:

(Jest to tzw. ciąg Fareya rzędu 9; takie ciągi mają wiele ciekawych własności, na omówienie których nie ma tu miejsca.)
Takich ułamków jest 27, a więc dzielą one przedział ![[0,1]](/math/temat/matematyka/teoria_liczb/2018/08/16/O_twierdzeniu_Slonimskiego/1x-c9361aa634d045cd9312ec3d8a778b17dd5d6b83-im-33,33,33-FF,FF,FF.gif) na 28 kawałków. Łatwo zauważyć, że dla każdej liczby rzeczywistej
na 28 kawałków. Łatwo zauważyć, że dla każdej liczby rzeczywistej 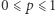 części całkowite liczb
części całkowite liczb 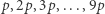 zależą tylko od tego, w którym z tych kawałków znajduje się liczba
zależą tylko od tego, w którym z tych kawałków znajduje się liczba 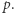 Przykładowo, dla liczby
Przykładowo, dla liczby 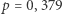 mamy
mamy

a więc:

i tak dalej. Cały ciąg części całkowitych wielokrotności 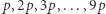 wygląda w tym przypadku tak:
wygląda w tym przypadku tak:

i łatwo zauważyć, że jest to ten sam ciąg, który pojawia się jako ciąg przeniesień 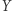 w pierwszej kolumnie tabeli wielokrotności liczby 379.
w pierwszej kolumnie tabeli wielokrotności liczby 379.
Liczba 28 jest na tyle niewielka, że wszystkie możliwe ciągi można ponumerować i umieścić na 28 kościach, jak u Napiera, albo - lepiej - na obracającym się cylindrze.
Zauważmy, że jeżeli podczas obliczania wielokrotności liczby wielocyfrowej znamy numer odpowiedniego (jednego z 28) ciągu cyfr 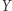 oraz aktualnie rozważaną cyfrę, to numer następnego ciągu jest jednoznacznie wyznaczony. W ten sposób, licząc od prawej do lewej, możemy kolejno dobierać ciągi cyfr
oraz aktualnie rozważaną cyfrę, to numer następnego ciągu jest jednoznacznie wyznaczony. W ten sposób, licząc od prawej do lewej, możemy kolejno dobierać ciągi cyfr 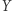 i obliczać kolejne cyfry wielokrotności danej liczby.
i obliczać kolejne cyfry wielokrotności danej liczby.

Urządzenie do mnożenia i jeden z cylindrów w tym urządzeniu.
Słonimski skonstruował proste urządzenie, które pozwala łatwo wykonać te operacje (rysunek). Widnieje na nim 11 rzędów okienek. W pierwszym rzędzie od dołu użytkownik, za pomocą pokręteł, ustawia cyfry liczby, której wielokrotności chce poznać. Następnie, poczynając od prawej strony, w trzecim rzędzie od dołu w danej kolumnie odczytuje kod (literę, jedną z 28) ciągu przeniesień. Następnie obraca inne pokrętło w następnej kolumnie po lewej, aż ten sam kod ukaże się w drugim rzędzie od dołu w tej kolumnie. Potem odczytuje kod w trzecim rzędzie od dołu i tak dalej, aż do pierwszej kolumny od lewej. Po wykonaniu tych czynności w pozostałych rzędach okienek można odczytać kolejne wielokrotności rozważanej liczby.
Centralnym elementem urządzenia Słonimskiego są specjalne cylindry, na których wypisane są wszystkie możliwe ciągi cyfr 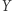 i które można odpowiednimi pokrętłami obracać i przesuwać w górę i w dół wzdłuż osi.
i które można odpowiednimi pokrętłami obracać i przesuwać w górę i w dół wzdłuż osi.
W 1844 r. Słonimski zaprezentował swoje urządzenie w Berlinie przed Pruską Królewską Akademią Nauk, a rok później w Petersburgu przed Cesarską Akademią Nauk, gdzie spotkał się z bardzo pozytywnym przyjęciem i otrzymał prestiżową Nagrodę Demidowa drugiego stopnia. Od cara Mikołaja I w uznaniu swoich zasług otrzymał też honorowe obywatelstwo, które wiązało się z prawem zamieszkania poza dzielnicą żydowską.
Poza swoją maszyną mnożącą Chaim Słonimski dokonał kilku innych ciekawych wynalazków. Zmarł w Warszawie; jego grób można znaleźć na Cmentarzu Żydowskim przy ul. Okopowej.
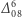 i
i