Mała Delta

Resztki

Skończyłam! - krzyknęła triumfalnie Agatka do swojego brata, Bartka. Dziewczynka regularnie domaga się od starszego chłopca rozmaitych ciekawostek matematycznych, których ten dowiaduje się w liceum...

Tym razem Bartek, aby uzyskać chwilę spokoju, przykazał jej (twierdząc, że jest w tym jakiś głębszy sens) umieścić w tabelce 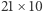$21 ×10$ liczby od 1 do 210 w taki sposób, aby numery wiersza i kolumny, w jakich znajdzie się dana liczba, odpowiadały jej resztom z dzielenia odpowiednio przez 21 i 10. - To było dość żmudne i jakoś nie wydaje mi się, by kryło się tu coś ciekawego…na pewno nie chciałeś się mnie po prostu pozbyć na chwilę?

$| ##### ############## ##### ##### ----|-1-##2##-3--##4###5####6##-7--##8##-9--##0## 1 | 1 #22## 43 #64###85##106# 127 #148# 169 #190# | ##### ############## ##### ##### #2###191##2###23##44###65##86###107##128##149##170# #3###171#192##3###24###45##66###87##108##129##150# | ##### ############## ##### ##### 4 |151 #172# 193 ##4###25##46## 67 #88## 109 #130# #5###131##152##173##194##5###26###47##68###89##110# #6###111##132##153##174##195###6###27##48###69###90# ################################################# #7##|91##112##133##154##175##196##7###28###49###70# #8###71##92###113##134##155##176##197###8###29###50# #9###51##72###93##114##135##156##177##198###9###30# | ##### ############## ##### ##### 10 |31 #52## 73 #94###115##136# 157 #178# 199 ##10## 11 |11 #32## 53 #74###95##116# 137 #158# 179 #200# ################################################# #12#|201##12###33##54###75##96###117##138##159##180# #13##181#202##13##34###55##76###97##118##139##160# #14##161#182#203##14###35##56###77##98###119##140# ################################################# #15#|141##162##183##204##15##36###57###78###99##120# 16 |121#142# 163 #184#205###16## 37 #58## 79 #100# 17 |101#122# 143 #164##185##206# 17 #38## 59 ##80# ################################################# #18#|81##102##123##144##165##186#207###18###39###60# 19 |61 #82## 103 #124##145##166# 187 #208# 19 ##40# 20 |41 #62## 83 #104##125##146# 167 #188#209 ##20# ################################################# #0###21##42###63##84###105##126##147##168##189##210#$

- Ależ skąd! - odpowiedział brat z udawanym oburzeniem. - Zauważ najpierw, że żadne dwie liczby nie zostały wpisane w tę samą komórkę. Gdyby bowiem tak się stało, to te dwie liczby dawałyby tę samą resztę z dzielenia przez $10$ i $21.$ W tej sytuacji ich różnica byłaby podzielna przez $|10$ i $21,$ a zatem przez $210$ (byłaby więc zerem), gdyż… - i tu Bartek teatralnie zawiesił głos.

- … gdyż są to liczby względnie pierwsze! - dokończyła prędko Agatka, ponieważ niedawno omawiali ten temat na kółku matematycznym. Po chwili dodała: - A skoro zarówno liczb, jak i komórek jest 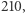$|210,$ więc w każdej komórce wyląduje jakaś liczba!

- Doskonale. - pochwalił siostrę Bartek. - Udowodniłaś właśnie Chińskie Twierdzenie o Resztach: każdy układ reszt z dzielenia przez parami względnie pierwsze liczby jest możliwy do zrealizowania. A skoro jesteśmy przy liczbach względnie pierwszych, zwróć uwagę na kolejną rzecz. Otóż jeśli wybierzesz dowolną liczbę względnie pierwszą z 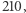$210,$ to jej wierszowa współrzędna jest względnie pierwsza z 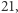$|21,$ a kolumnowa z 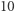$|10$ i odwrotnie: każda taka para współrzędnych określa liczbę względnie pierwszą z 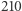$210$ (dowód nie jest trudny, spróbuj sama!). - mówiąc to, Bartek zamalował na kolorowo wszystkie liczby, które nie były względnie pierwsze z 210. 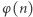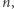- W tej sytuacji, jeśli przez $|φ(n)$ oznaczymy liczbę liczb mniejszych od $n$ i względnie pierwszych z $n,$ to musi zachodzić 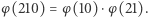$φ (210) = φ(10) ⋅φ(21).$ Podobna zależność zachodzi z tych samych względów dla iloczynu dowolnych dwóch liczb względnie pierwszych.

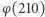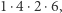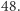- Wspaniale! - wykrzyknęła Agatka. - W tej sytuacji $φ(210)$ wynosi $|1⋅4⋅2 ⋅6,$ czyli $|48.$ Nie mogłeś mi tego wszystkiego powiedzieć bez tej upiornej tabelki…?