Drobiazgi

Rozsądnego algorytmu brak

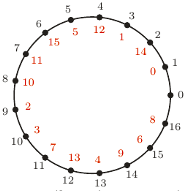
Na obrazku widać przenumerowanie szesnastu z 17 równo rozmieszczonych punktów na okręgu. Obok "normalnych" czarnych numerków podano dziwnie rozmieszczone czerwone. Zrobiono to w ten sposób, że nawinięto na ten okrąg półprostą, na której zaznaczono punkty odpowiadające kolejnym potęgom 3.

I rzeczywiście mamy: 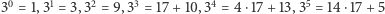$0 1 2 3 4 5 3 = 1,3 = 3,3 = 9,3 = 17 + 10, 3 = 4⋅17 +13,3 = 14⋅17 +5$ i tak dalej, czyli 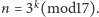$|n = 3k(mod17).$ Czytelnik zechce sprawdzić ten przepis dla kolejnych wykładników.

Ciekawe, że każdy z "czarnych" punktów, poza 0, dostał nową etykietkę.

Można spróbować zastosować podobny przepis dla innej podstawy potęg i innej liczby równomiernie na okręgu rozmieszczonych punktów. Zważywszy nasze codzienne przyzwyczajenia, najwygodniej jest nam potęgować 10, a liczbę punktów ustalmy, powiedzmy, na 7 i obliczajmy reszty modulo 7.

Mamy

0 1 2 3 10 ≡1,10 ≡ 3,10 ≡ 2,10 ≡ 6,

kolejne reszty to 4 i 5 - są wszystkie, a więc jest ich sześć, czyli każdy "czarny punkt" poza 0 otrzyma czerwoną etykietę.

Gdybyśmy jednak zamiast 7 wzięli 3 punkty na okręgu, to i tak tylko jeden z nich otrzymałby przy potęgowaniu 10 czerwoną etykietę.

Trzymając się potęgowania 10, dla 11 czerwone etykiety otrzymałyby tylko dwa punkty, a dla 13 sześć.

Natomiast przy tym potęgowaniu wszystkie czarne punkty otrzymałyby czerwone etykiety dla 17 (tak jak przy potęgowaniu 3), 19, 29, 97 czy 337. Zdaję sobie sprawę, jak trudno to sprawdzić.

Choć mogę podać równoważny sposób badania tego problemu: z potęgowania liczby 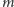$|m$ otrzymamy wszystkie reszty modulo 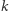$k |$ wtedy i tylko wtedy, gdy rozwinięcie liczby 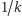$1/k |$ w ułamek o podstawie 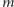$m$ będzie miało okres długości 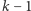$|k− 1$ , czyli taka jest długość okresu, jaka jest liczba niezerowych reszt. Np. 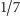$|1/7$ w systemie dziesiętnym to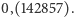 $0,(142857).$

Czy to pomaga stwierdzić, kiedy wszystkie reszty się pojawiają? Można wątpić - nie sądzę, aby każdy Czytelnik stwierdził bez trudu, że np. 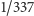$|1/337$ ma okres długości 336.

Oczywiście, dla każdej podstawy $|m$ można obliczyć, czy jej potęgi dają wszystkie niezerowe reszty modulo 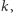$k,|$ ale robi się to, po prostu potęgując i dzieląc: podane tutaj dwie metody nie różnią się niczym - tylko w pierwszym przypadku zapisujemy reszty, a w drugim ilorazy. Cóż za piękna okazja, by znaleźć lepszy algorytm i wsławić się na wieki, bo problem postawił Gauss, a informacji o nim należy szukać pod hasłem pierwiastki pierwotne.