Przerwy w liczbach pierwszych

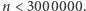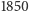Najpierw trochę historii. W 1845 roku Joseph Bertrand sformułował hipotezę twierdzącą, że "odległość od najbliższej liczby pierwszej nie może być większa niż liczba, od której zaczynamy poszukiwania". Dlatego też niekiedy omawiane twierdzenie nazywane jest hipotezą Bertranda. Sam Bertrand udowodnił swoją hipotezę dla liczb $n < 3000000.$ W $1850$ roku Pafnutij Czebyszew znalazł pierwszy pełny dowód dla wszystkich liczb naturalnych. My przedstawimy dowód autorstwa słynnego Paula Erdösa, który publikując go w 1932 roku, miał zaledwie 19 lat.

Najpierw wykażemy prawdziwość twierdzenia dla liczb 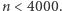$|n < 4000.$ Zauważmy, że nie musimy sprawdzać wszystkich przypadków, a wystarczy jedynie wskazać ciąg liczb pierwszych, z których każda jest mniejsza niż dwukrotność poprzedniej. Przykładowy taki ciąg to

2,3,5,7,13,23,43,83,163,317,631,1259,2503,4001.

Zajmijmy się więc dowodem dla 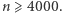$| n ⩾ 4000.$ W tym celu będziemy przyglądać się liczbie 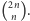$2n (n).$ Oszacujemy ją z dołu i z góry. Następnie okaże się, że przy założeniu, że nie ma żadnych liczb pierwszych w przedziale $|(n,2n],$ dojdziemy do sprzeczności.

Wykażmy na początek dosyć proste oszacowanie dolne. Dla dowolnego 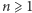$|n⩾ 1$ zachodzi

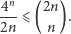n 4--⩽ (2n ). 2n n

(1)

Jest tak, gdyż 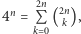$2n 4n = P (2nk), k 0$ a wartość 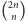$(2nn)$ jest największą spośród 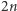$|2n$ liczb: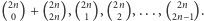 $2n 2n 2n 2n 2n |(0) + (2n),( 1 ),(2),...,(2n−1).$

Przejdziemy teraz do oszacowania górnego, które otrzymamy w kilku krokach. Pierwsze oszacowanie, które będzie nam pomocne za moment, jest samo w sobie bardzo interesujące. Pokażemy, że

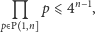M p ⩽ 4n−1, p> P 1,n

(2)

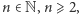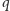dla wszystkich $n ∈ N,n ⩾ 2,$ gdzie $P(i, j]$ to zbiór zawierający wszystkie liczby pierwsze w przedziale $(i, j].$ Zauważmy najpierw, że wystarczy udowodnić ten fakt tylko dla liczb pierwszych. Wówczas niech $q$ będzie największą liczbą pierwszą nie większą niż $|n.$ Dostajemy

q− 1 n−1 M p = M p ⩽ 4 ⩽4 . p>P 1,n p> P 1,q

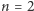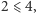Udowodnimy więc (2) przez indukcję. Dla $n = 2$ mamy $2 ⩽ 4,$ więc jest to prawda. Aby wykonać krok indukcyjny, załóżmy, że nierówność (2) jest prawdziwa dla wszystkich liczb pierwszych mniejszych od liczby pierwszej 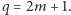$|q = 2m + 1.$ Mamy

2m + 1 M p = M p ⋅ M p ⩽4m(⋅ ) ⩽ 4m22m= 42m. p> P 1,2m+1 p>P 1,m+1 p> P m+1,2m+1 m

Nierówność

M p ⩽4m p> P 1,m+1

wynika z założenia indukcyjnego. Nierówność

p ⩽ (2m + 1) = (2m-+-1)!-- p> P mM+2,2m+1 m m!(m + 1)!

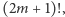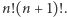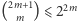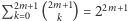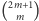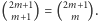
natomiast wynika z tego, że wszystkie liczby pierwsze w $P(m +1,2m + 1]$ dzielą licznik $| (2m + 1)!,$ ale nie dzielą mianownika $| n!(n +1)!.$ Ostatnia nierówność $2m+1 2m |( m) ⩽2$ wynika zaś z tego, że $2m+1 2m+1 2m+1 P | k 0 ( k ) = 2$ oraz dwa z tych wyrazów to $|(2m+m1)$ i $(2mm++11) = (2mm+)1.$

Przypomnijmy teraz twierdzenie Legendre'a, mówiące, że w rozkładzie liczby 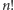$|n!$ na czynniki pierwsze liczba pierwsza 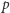$p$ pojawia się dokładnie 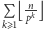$|P ⌊nk⌋ kE1 p$ razy. Łatwo je udowodnić, zauważając, że w iloczynie 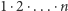$|1⋅2⋅...⋅n$ dokładnie 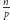$|np$ liczb jest podzielnych przez 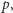$p,$ dokładnie 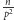$np2$ jest podzielnych przez 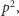$|p2,$ itd.

Przypomnijmy też, że 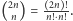$(2n) = 2n--!. n n!⋅n!$ Z twierdzenia Legendre'a łatwo wywnioskować, że dowolna liczba pierwsza dzieli 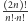$2n- ! n!⋅n!$ w potędze dokładnie

Q (⌊ 2n⌋ − 2⌊n-⌋) . kE1 pk pk

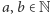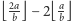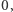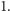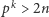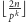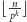Dla dowolnych liczb $a,b ∈ N$ liczba $2a a |⌊b⌋ − 2⌊b⌋$ jest równa albo $|0,$ albo $|1.$ Dodatkowo dla $pk > 2n$ wartości $⌊2nk⌋ p$ oraz $|⌊nk⌋ p$ są równe zeru. Zatem otrzymujemy, że liczba pierwsza 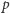$p$ dzieli 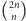$2n ( n)$ w potędze dokładnie

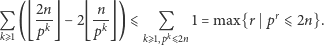2n n r Q ( ⌊-k-⌋− 2⌊-k-⌋)⩽ Q 1 = max{r p ⩽2n}. kE1 p p kE1,pkD2n

(3)

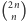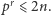Możemy więc przejść do właściwego oszacowania. Będziemy się zastanawiać, ile razy różne liczby pierwsze występują w rozkładzie $|(2nn)$ na czynniki pierwsze. Zauważmy najpierw, że z (3) wynika, iż dla dowolnego $|p∈ P(1,n]$ potęga $r$ jest taka, że $|pr⩽ 2n.$ A więc w szczególności liczby pierwsze 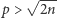$| √ --- p > 2n$ występują tam co najwyżej jeden raz. Istotne jest spostrzeżenie, że liczby pierwsze 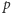$p$ spełniające 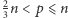$|23n < p ⩽ n$ wcale nie dzielą 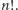$|n!.$ Jest tak, gdyż dzielą zarówno licznik 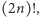$|(2n)!,$ jak i mianownik 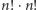$|n!⋅n!$ w potędze równej dwa. Otrzymujemy więc

2n ( )⩽ M --2n ⋅ M -- p ⋅ M p. n p> P 1, 2n p> P 2n,23n p> P n,2n

W połączeniu z (1) mamy

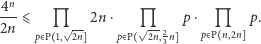4n- 2n ⩽ M --2n ⋅ M --2 p ⋅ M p. p> P 1, 2n p> P 2n,3n p> P n,2n

(4)

Przypuśćmy teraz, że dla pewnego 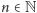$n ∈N$ zbiór $|P(n,2n]$ jest pusty. Wówczas z (4) wynika, że

4n -- 2 ---⩽ M 2n ⋅ M p ⩽ (2n) 2n ⋅43n, 2n p> P 1, 2n p>P 2n,23n

gdzie druga nierówność wynika z (2). Przekształcając, otrzymujemy

-- 4n ⩽ (2n) 2n+1⋅423n

oraz

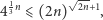1n 2n+1 43 ⩽ (2n) ,

(5)

co, jak zaraz wykażemy, nie jest prawdą dla 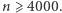$|n⩾ 4000.$

Korzystając z nierówności 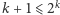$|k+ 1 ⩽2k$ prawdziwej dla 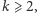$k ⩾ 2,$ mamy

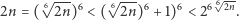6√ ---6 √6---6 6 66 2n 2n = ( 2n) < ( 2n) + 1) < 2 .

(6)

Dla liczb 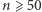$n ⩾ 50$ dostajemy

2n 3 1+ 2n 66 2n3 1+ 2 186 2n 1+ 2 206 2n 2 20 2n 23 2 ⩽(2n) < 2 = 2 < 2 = 2 ,

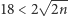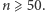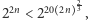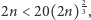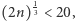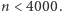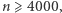gdzie pierwsza nierówność wynika z (5), następna z (6), a ostatnia z faktu, że $--- 18 < 2√ 2n$ dla $n ⩾ 50.$ Mamy więc $22n < 220 2n 23,$ czyli $2 |2n < 20(2n) 3,$ czyli $1 |(2n)3 < 20,$ czyli $|n < 4000.$ A zatem zbiór $|P(n,2n]$ nie może być pusty dla liczb $n ⩾ 4000,$ co kończy dowód twierdzenia Czebyszewa.