Jedno zdanie
O trudnym problemie, który ma jednozdaniowe rozwiązanie...
Problem. Nieparzysta liczba pierwsza 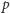 może być przedstawiona jako suma dwóch kwadratów liczb naturalnych
może być przedstawiona jako suma dwóch kwadratów liczb naturalnych
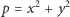 |
(1) |
wtedy i tylko wtedy jeśli 
Taką hipotezę postawił w 1625 roku Albert Girard, a w 1640 roku również Pierre de Fermat i to z jego powodu ten fakt nazywany jest teraz twierdzeniem Fermata o sumie dwóch kwadratów.
Jednak żaden z powyższych matematyków nie udowodnił postawionej hipotezy. Zrobił to dopiero w 1747 roku Leonard Euler, jego dowód był jednak dosyć skomplikowany. Potem pojawiały się kolejne, coraz prostsze dowody, udział wzięli m.in. Lagrange w 1775 roku i Dedekind w 1877 roku. Aż w końcu parę lat temu, w roku 1990, Don Zagier, amerykański matematyk, przedstawił dowód, który miał dokładnie jedno zdanie. Aby je wystarczy przeczytać artykuł z The American Mathematical Monthly, Vol. 97, No. 2.
Przedstawimy tutaj ten dowód w nieco większej, ale wciąż małej liczbie zdań. Po pierwsze, zauważmy, że jeśli  i
i 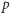 jest nieparzysta, to
jest nieparzysta, to  Zatem w oczywisty sposób
Zatem w oczywisty sposób  nie jest sumą dwóch kwadratów, bo każdy kwadrat przystaje do 0 lub
nie jest sumą dwóch kwadratów, bo każdy kwadrat przystaje do 0 lub  modulo
modulo 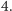
Ustalmy taką liczbę 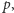 że
że 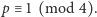 Do dowodu twierdzenia wystarczy wykazać, że równanie
Do dowodu twierdzenia wystarczy wykazać, że równanie 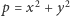 ma przynajmniej jedno rozwiązanie. Przyjrzyjmy się dokładniej innemu równaniu
ma przynajmniej jedno rozwiązanie. Przyjrzyjmy się dokładniej innemu równaniu
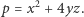 |
(2) |
Wykażemy, że ma ono nieparzyście wiele rozwiązań. Nim to jednak zrobimy zobaczmy, jak z tego wynika, że 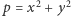 ma rozwiązanie. Zauważmy, że jeśli
ma rozwiązanie. Zauważmy, że jeśli 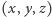 jest rozwiązaniem (2), to
jest rozwiązaniem (2), to 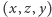 również. A więc rozwiązania równania (2) łączą się w pary, oprócz takich rozwiązań, że
również. A więc rozwiązania równania (2) łączą się w pary, oprócz takich rozwiązań, że 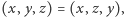 czyli gdy
czyli gdy 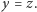 Ponieważ, jak wykażemy wkrótce, rozwiązań (2) jest nieparzyście wiele, to nie wszystkie mogą połączyć się w pary i istnieje pewne rozwiązanie takie, że
Ponieważ, jak wykażemy wkrótce, rozwiązań (2) jest nieparzyście wiele, to nie wszystkie mogą połączyć się w pary i istnieje pewne rozwiązanie takie, że 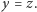 A to oznacza, że mamy
A to oznacza, że mamy 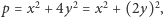 czyli również (1) ma rozwiązanie.
czyli również (1) ma rozwiązanie.
Żeby wykazać, że (2) ma nieparzyście wiele rozwiązań, stosujemy podobną metodę co poprzednio. Rozważmy przekształcenie
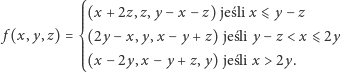 |
(3) |
Okazuje się, że jeśli  rozwiązuje równanie (2), to
rozwiązuje równanie (2), to 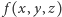 również, ponadto po dwukrotnym zastosowaniu funkcji
również, ponadto po dwukrotnym zastosowaniu funkcji 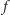 do trójki
do trójki 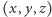 otrzymujemy ponownie
otrzymujemy ponownie 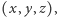 co Czytelnik Cierpliwy może sprawdzić samodzielnie. A więc funkcja
co Czytelnik Cierpliwy może sprawdzić samodzielnie. A więc funkcja  może nam posłużyć do sparowania rozwiązań równania (2):
może nam posłużyć do sparowania rozwiązań równania (2): 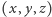 jest w parze z
jest w parze z 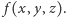 Jedyne rozwiązania, które nie stoją w parach, to te, dla których
Jedyne rozwiązania, które nie stoją w parach, to te, dla których 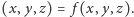 Okazuje się, że takie rozwiązania można jedynie otrzymać za pomocą środkowej linii definicji (3), czyli dla
Okazuje się, że takie rozwiązania można jedynie otrzymać za pomocą środkowej linii definicji (3), czyli dla
 |
(4) |
Łatwo sprawdzić, że linia pierwsza i trzecia dawałaby 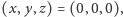 co oczywiście nie spełnia równania (2). Dla (4) otrzymujemy
co oczywiście nie spełnia równania (2). Dla (4) otrzymujemy 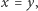 czyli
czyli 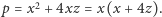 Musi to oznaczać
Musi to oznaczać 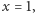 więc
więc 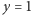 oraz
oraz  czyli jest tylko jedno rozwiązanie (2), które nie stoi w parze:
czyli jest tylko jedno rozwiązanie (2), które nie stoi w parze: 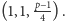 A zatem rozwiązań (2) jest nieparzyście wiele, co kończy dowód.
A zatem rozwiązań (2) jest nieparzyście wiele, co kończy dowód.