Liczby pierwsze jako niewiadome
W historii ludzkiego poznania mało jest tak fascynujących pojęć jak liczby pierwsze. Chociaż dzisiaj wiemy o nich znacznie więcej niż 120 lat temu, to jeszcze więcej dotyczących ich pytań pozostaje bez odpowiedzi. Celem tej notki jest pokazanie, że trudno jest ocenić na pierwszy rzut oka, czy pytanie dotyczące liczb pierwszych jest łatwe, czy też bardzo trudne - poza zasięgiem współczesnej nauki.

Rozważmy najpierw następujące równanie z dwiema niewiadomymi:
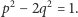 |
(1) |
Szukamy rozwiązań w liczbach pierwszych 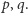 Jeśli
Jeśli 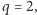 to
to 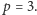 Jeżeli natomiast
Jeżeli natomiast 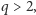 to obie
to obie 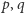 są nieparzyste, a więc
są nieparzyste, a więc

Wynika stąd, że

co jest absurdem. Jedynym rozwiązaniem równania (1) w liczbach pierwszych 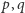 jest zatem para
jest zatem para 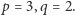
Zajmiemy się teraz podobnym równaniem:
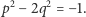 |
(2) |
Można zgadnąć, że para 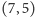 jest rozwiązaniem (2) w liczbach pierwszych. W przypadku jeszcze większej determinacji natrafimy na rozwiązanie
jest rozwiązaniem (2) w liczbach pierwszych. W przypadku jeszcze większej determinacji natrafimy na rozwiązanie 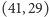 (proszę sprawdzić!) ale co robić dalej! Już teraz widać, że ewentualny dowód (ewentualnego) "twierdzenia", iż równanie (2) ma tylko skończenie wiele rozwiązań w liczbach pierwszych
(proszę sprawdzić!) ale co robić dalej! Już teraz widać, że ewentualny dowód (ewentualnego) "twierdzenia", iż równanie (2) ma tylko skończenie wiele rozwiązań w liczbach pierwszych 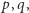 nie może być całkiem banalny, gdyż musiałby on wychwycić znalezione rozwiązania. Podejdźmy więc do problemu bardziej systematycznie i bez żadnych uprzedzeń. Zauważmy przede wszystkim, że pary
nie może być całkiem banalny, gdyż musiałby on wychwycić znalezione rozwiązania. Podejdźmy więc do problemu bardziej systematycznie i bez żadnych uprzedzeń. Zauważmy przede wszystkim, że pary 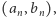 określone wzorem
określone wzorem

spełniają równanie (2), gdyż ze wzoru dwumianowego Newtona wynika, że

a zatem

gdyż  jest nieparzyste. Łatwo sprawdzić, że zgadnięte wcześniej rozwiązania w liczbach pierwszych to
jest nieparzyste. Łatwo sprawdzić, że zgadnięte wcześniej rozwiązania w liczbach pierwszych to 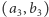 oraz
oraz 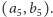 Z pomocą komputera sprawdziliśmy rozwiązania
Z pomocą komputera sprawdziliśmy rozwiązania 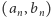 dla wszystkich
dla wszystkich 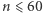 : tylko dla
: tylko dla 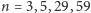 otrzymujemy obie liczby pierwsze.
otrzymujemy obie liczby pierwsze.

Ale możemy zaryzykować hipotezę, że równanie (2) ma nieskończenie wiele rozwiązań w liczbach pierwszych 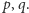 Raczej nie zachęcamy Cię, Czytelniku, abyś się nią zajmował, ale do studiowania matematyki teoretycznej jak najbardziej:)
Raczej nie zachęcamy Cię, Czytelniku, abyś się nią zajmował, ale do studiowania matematyki teoretycznej jak najbardziej:)