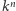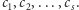Kongruencje z królikiem
Artykuł o powyższym tytule wypada rozpocząć od przypomnienia, czym są kongruencje. Jeśli dwie liczby naturalne  i
i 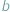 dają tę samą resztę z dzielenia przez liczbę naturalną
dają tę samą resztę z dzielenia przez liczbę naturalną  (innymi słowy, jeśli
(innymi słowy, jeśli  jest podzielne przez
jest podzielne przez 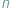 ), uczenie jest stwierdzić, że
), uczenie jest stwierdzić, że 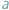 i
i 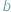 przystają do siebie modulo
przystają do siebie modulo 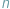 i fakt ten zanotować jako
i fakt ten zanotować jako  W tym kontekście znaczek "
W tym kontekście znaczek "  " (lub raczej to, co on sobą reprezentuje) nazywamy właśnie kongruencją.
" (lub raczej to, co on sobą reprezentuje) nazywamy właśnie kongruencją.

Kongruencje mają wiele wdzięcznych własności, między innymi można je dodawać i mnożyć stronami tak jak zwykłe równania. Ich zastosowanie pozwala uprościć zawiłe nieraz rozumowania z zakresu teorii liczb. W moim artykule chciałbym skoncentrować się na problemach dotyczących początkowych cyfr liczb postaci  gdzie
gdzie  i
i 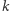 są liczbami naturalnymi. Rozpocznę od rozwiązania zadania, które skłoniło mnie do takich rozważań.
są liczbami naturalnymi. Rozpocznę od rozwiązania zadania, które skłoniło mnie do takich rozważań.
Rozwiązanie. Najpierw zauważmy, że dla dowolnego  mamy
mamy 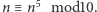 Istotnie, niech
Istotnie, niech 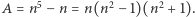 Jeśli
Jeśli  jest podzielne przez 5, to oczywiście 5 dzieli również
jest podzielne przez 5, to oczywiście 5 dzieli również 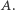 Z drugiej strony, jeśli
Z drugiej strony, jeśli 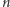 nie jest podzielne przez 5, to rozpatrując wszystkie niezerowe reszty z dzielenia
nie jest podzielne przez 5, to rozpatrując wszystkie niezerowe reszty z dzielenia 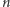 przez 5, możemy się przekonać, że
przez 5, możemy się przekonać, że 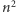 daje resztę 1 lub 4 z dzielenia przez 5 i w obu przypadkach 5 dzieli
daje resztę 1 lub 4 z dzielenia przez 5 i w obu przypadkach 5 dzieli 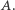 W analogiczny (a nawet prostszy) sposób pokazujemy, że
W analogiczny (a nawet prostszy) sposób pokazujemy, że  jest zawsze podzielne przez 2, skąd wnioskujemy podzielność
jest zawsze podzielne przez 2, skąd wnioskujemy podzielność 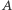 przez 10 i
przez 10 i  dla dowolnej liczby naturalnej
dla dowolnej liczby naturalnej 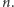 Zauważmy, że jeśli będziemy mnożyć tę kongruencję obustronnie przez
Zauważmy, że jeśli będziemy mnożyć tę kongruencję obustronnie przez 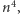 otrzymamy ciąg kongruencji
otrzymamy ciąg kongruencji
 |
Teraz już rozważamy tylko te potęgi 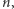 których wykładnik daje resztę 1 z dzielenia przez 4. Dzięki temu ostatnia cyfra
których wykładnik daje resztę 1 z dzielenia przez 4. Dzięki temu ostatnia cyfra  liczby
liczby 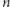 będzie cyfrą, którą chcemy otrzymać jako pierwszą cyfrę liczby
będzie cyfrą, którą chcemy otrzymać jako pierwszą cyfrę liczby 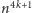 dla pewnego
dla pewnego  Chcemy zatem uzyskać
Chcemy zatem uzyskać

Po przyłożeniu do obu stron logarytmu dziesiętnego dostajemy równoważną postać

Dzięki zlogarytmowaniu nasz problem wygląda następująco: mamy nieskończenie długą drogę, na której co 1 mamy dziurę długości

począwszy od 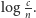 Po tej nieskończonej drodze skacze królik, który rozpoczyna w 0 i robi skoki długości
Po tej nieskończonej drodze skacze królik, który rozpoczyna w 0 i robi skoki długości 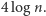 Chcemy pokazać, że nasz królik wpadnie kiedyś do dziury. Innymi słowy, potrzebujemy uzasadnić, że
Chcemy pokazać, że nasz królik wpadnie kiedyś do dziury. Innymi słowy, potrzebujemy uzasadnić, że

gdzie 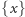 oznacza część ułamkową liczby
oznacza część ułamkową liczby 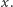 Zauważmy najpierw, że dla różnych liczb naturalnych
Zauważmy najpierw, że dla różnych liczb naturalnych 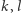 liczby
liczby  oraz
oraz  są różne. W przeciwnym przypadku istniałoby takie
są różne. W przeciwnym przypadku istniałoby takie 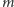 naturalne, że
naturalne, że 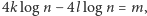 czyli
czyli 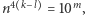 co przeczy założeniu o niepodzielności
co przeczy założeniu o niepodzielności  przez 10. Rozważmy teraz liczby
przez 10. Rozważmy teraz liczby 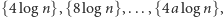 gdzie
gdzie  to pewna liczba naturalna, która jest większa od
to pewna liczba naturalna, która jest większa od 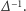 Skoro wypisane liczby są różne, to pewne dwie leżą w odległości mniejszej niż
Skoro wypisane liczby są różne, to pewne dwie leżą w odległości mniejszej niż 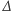 (odległość liczb
(odległość liczb 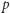 i
i 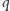 należy tu rozumieć jako mniejszą z liczb
należy tu rozumieć jako mniejszą z liczb  oraz
oraz 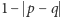 ). Oznaczmy je przez
). Oznaczmy je przez 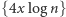 oraz
oraz  gdzie
gdzie 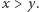 W tej sytuacji liczba
W tej sytuacji liczba 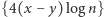 leży w przedziale
leży w przedziale 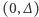 lub
lub  Patrząc na ciąg
Patrząc na ciąg  widzimy teraz, że dla początkowych wyrazów jest on ściśle monotoniczny i dla pewnego
widzimy teraz, że dla początkowych wyrazów jest on ściśle monotoniczny i dla pewnego 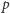 naturalnego otrzymamy
naturalnego otrzymamy 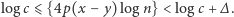 Wystarczy więc przyjąć
Wystarczy więc przyjąć 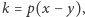 aby zakończyć rozwiązanie zadania.
aby zakończyć rozwiązanie zadania.
W powyższym dowodzie można wyróżnić dwie istotne części: pierwsza polega na wskazaniu podciągu potęg 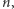 które kończą się tą samą cyfrą, a w drugiej pokazaliśmy, że dowolna cyfra może stać na początku pewnego wyrazu tego podciągu. Tę drugą część można nietrudno zmodyfikować tak, aby wykazać poniższe:
które kończą się tą samą cyfrą, a w drugiej pokazaliśmy, że dowolna cyfra może stać na początku pewnego wyrazu tego podciągu. Tę drugą część można nietrudno zmodyfikować tak, aby wykazać poniższe:
Twierdzenie 1. Dla dowolnej liczby naturalnej  która nie jest potęgą dziesiątki, i dowolnego ciągu cyfr
która nie jest potęgą dziesiątki, i dowolnego ciągu cyfr 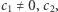
 istnieje liczba naturalna
istnieje liczba naturalna  dla której początkowe cyfry liczby
dla której początkowe cyfry liczby 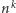 to
to 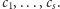
Z powyższego twierdzenia wynika, że dla dowolnego 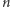 możemy znaleźć
możemy znaleźć 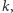 dla którego
dla którego 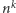 będzie się rozpoczynało, na przykład, od cyfr 100000, czyli będzie dość bliskie pewnej potędze dziesiątki. Warto zwrócić uwagę, że możemy oszacować wykładnik tej potęgi
będzie się rozpoczynało, na przykład, od cyfr 100000, czyli będzie dość bliskie pewnej potędze dziesiątki. Warto zwrócić uwagę, że możemy oszacować wykładnik tej potęgi 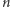 niezależnie od
niezależnie od 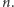
Twierdzenie 2. Jeśli  jest liczbą naturalną niepodzielną przez 10, to dla dowolnego
jest liczbą naturalną niepodzielną przez 10, to dla dowolnego 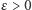 istnieją takie liczby naturalne
istnieją takie liczby naturalne 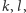 że
że 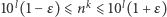 oraz
oraz 
Dowód. Żądamy od naszego 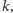 aby
aby

dla pewnego naturalnego 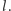 Ponownie równoważnie
Ponownie równoważnie

więc

Łatwo wykazać, że

więc wystarczające jest, aby

Dalej postępujemy tak jak poprzednio - kolejne liczby postaci 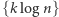 są różne, zatem wśród pierwszych
są różne, zatem wśród pierwszych 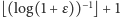 pewne dwie znajdują się w odległości mniejszej od
pewne dwie znajdują się w odległości mniejszej od 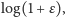 a ich różnica jest szukaną wielokrotnością
a ich różnica jest szukaną wielokrotnością 

Należy podkreślić, że opisana w twierdzeniu liczba 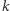 jest nie większa od
jest nie większa od  Na przykład, biorąc
Na przykład, biorąc 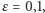 otrzymujemy, że dla dowolnej liczby
otrzymujemy, że dla dowolnej liczby  istnieje liczba
istnieje liczba 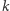 nie większa od
nie większa od 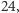 taka, że
taka, że  można przybliżyć potęgą dziesiątki z dokładnością do
można przybliżyć potęgą dziesiątki z dokładnością do 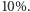 Przykładową wartością
Przykładową wartością  dla której przedstawione oszacowanie jest optymalne, jest
dla której przedstawione oszacowanie jest optymalne, jest 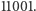 Podobny rezultat możemy, oczywiście, uzyskać, rozważając przybliżenia potęgami innych liczb naturalnych niż 10. Przykładowo, dla
Podobny rezultat możemy, oczywiście, uzyskać, rozważając przybliżenia potęgami innych liczb naturalnych niż 10. Przykładowo, dla  przybliżamy
przybliżamy 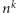 z dokładnością do
z dokładnością do 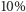 liczbą postaci
liczbą postaci 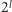 i wystarczy do tego
i wystarczy do tego  nie większe niż 7.
nie większe niż 7.
Wróćmy do naszych początkowych cyfr. Wydaje się, że ciągi liczb, które nie są jakoś szczególnie zbudowane, mogą rozpoczynać się dowolnymi cyframi. Oczywiście, nie jestem w stanie udowodnić powyższego, bo cóż to są "szczególne ciągi"? Oto kolejny przykład liczb, które mogą rozpoczynać się od dowolnych cyfr:
Szkic dowodu. Jeśli 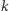 jest dość duże, to
jest dość duże, to 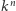 i
i 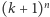 zbyt wiele się nie różnią (względnie), gdyż iloraz
zbyt wiele się nie różnią (względnie), gdyż iloraz  staje się dowolnie bliski 1, zatem z czasem różnica jest mniejsza niż różnica między elementami ciągu geometrycznego o dowolnie małym ilorazie większym od 1. Teraz logarytmując, otrzymamy "królika", który robi skoki o długości malejącej do 0, więc z pewnością wpadnie do naszych dziur.
staje się dowolnie bliski 1, zatem z czasem różnica jest mniejsza niż różnica między elementami ciągu geometrycznego o dowolnie małym ilorazie większym od 1. Teraz logarytmując, otrzymamy "królika", który robi skoki o długości malejącej do 0, więc z pewnością wpadnie do naszych dziur.
Ogólniej, dowolny ciąg liczb naturalnych 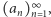 dla którego granica ciągu
dla którego granica ciągu 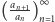 jest równa 1 ma tę własność, że dowolny skończony ciąg cyfr stanowi początkowe cyfry w zapisie dziesiętnym pewnego wyrazu ciągu
jest równa 1 ma tę własność, że dowolny skończony ciąg cyfr stanowi początkowe cyfry w zapisie dziesiętnym pewnego wyrazu ciągu 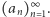 Przykładem takiego ciągu jest również ciąg kolejnych liczb pierwszych (co wynika z klasycznego, lecz wielce nieoczywistego twierdzenia o liczbach pierwszych). Zachęcam Czytelników do poszukiwania innych ciągów, których prefiksy mogą być dowolnie ustalonym ciągiem cyfr.
Przykładem takiego ciągu jest również ciąg kolejnych liczb pierwszych (co wynika z klasycznego, lecz wielce nieoczywistego twierdzenia o liczbach pierwszych). Zachęcam Czytelników do poszukiwania innych ciągów, których prefiksy mogą być dowolnie ustalonym ciągiem cyfr.