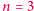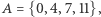Od Prouheta–Tarry'ego–Escotta do Thuego–Morse'a
Do jednych z najstarszych problemów w historii matematyki należy niewątpliwie zaliczyć równania diofantyczne, czyli równania o dziedzinie rozwiązań ograniczonej do liczb całkowitych. Obecną nazwę zawdzięczają one Diofantosowi, greckiemu matematykowi żyjącemu w III wieku naszej ery w Aleksandrii. Swoje rozważania na temat takich równań Diofantos zawarł w serii ksiąg pod tytułem Arytmetyka. Studiując jedną z nich, Pierre de Fermat - żyjący w XVII wieku francuski prawnik i matematyczny samouk - uznał, że pewne zawarte w niej równanie nie może mieć rozwiązań, o czym raczył poinformować przyszłych czytelników w słynnej uwadze, zamieszczonej na marginesie (czytanej przezeń książki oraz niniejszego artykułu).
Mowa, rzecz jasna, o równaniu 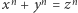 dla
dla 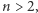 które czekało na rozwiązanie (a właściwie dowód jego braku) ponad 300 lat. Dopiero w 1993 roku, po kilku latach intensywnych prac, Andrew Wiles zakończył wysiłek pokoleń matematyków, dowodząc postawionej na początku drugiej połowy XX wieku hipotezy Shimury-Taniyamy. Po licznych poprawkach jego rozumowanie zostało w roku 1995 oficjalnie opublikowane na łamach Annals of Mathematics, a w 2016 roku został on uhonorowany prestiżową Nagrodą Abela.
które czekało na rozwiązanie (a właściwie dowód jego braku) ponad 300 lat. Dopiero w 1993 roku, po kilku latach intensywnych prac, Andrew Wiles zakończył wysiłek pokoleń matematyków, dowodząc postawionej na początku drugiej połowy XX wieku hipotezy Shimury-Taniyamy. Po licznych poprawkach jego rozumowanie zostało w roku 1995 oficjalnie opublikowane na łamach Annals of Mathematics, a w 2016 roku został on uhonorowany prestiżową Nagrodą Abela.
Wielkie Twierdzenie Fermata dotyczy prostego w sformułowaniu równania diofantycznego, którego rozwiązanie wymaga zastosowania bardzo zaawansowanych narzędzi matematycznych. W niniejszym artykule chciałbym przedstawić zgoła przeciwną sytuację: pozornie skomplikowane równanie diofantyczne przeanalizujemy przy użyciu metod elementarnych. Rozważmy następujący układ równań diofantycznych:
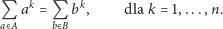 |
gdzie 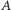 oraz
oraz 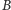 są pewnymi dwoma równolicznymi i rozłącznymi skończonymi zbiorami liczb całkowitych oraz
są pewnymi dwoma równolicznymi i rozłącznymi skończonymi zbiorami liczb całkowitych oraz 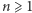 jest liczbą naturalną. Należy więc dla ustalonego wykładnika
jest liczbą naturalną. Należy więc dla ustalonego wykładnika 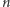 znaleźć takie dwa równoliczne i rozłączne zbiory liczb całkowitych
znaleźć takie dwa równoliczne i rozłączne zbiory liczb całkowitych  i
i 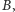 by sumy liczb z tych zbiorów w potęgach mniejszych lub równych
by sumy liczb z tych zbiorów w potęgach mniejszych lub równych 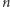 były równe. Problem ten pochodzi od Eulera i Goldbacha, współcześnie znany jest pod nazwą problemu Prouheta-Tarry'ego-Escotta. Prouhet zajmował się tym układem w połowie XIX wieku, pozostali na początku XX wieku podali wiele interesujących rozwiązań.
były równe. Problem ten pochodzi od Eulera i Goldbacha, współcześnie znany jest pod nazwą problemu Prouheta-Tarry'ego-Escotta. Prouhet zajmował się tym układem w połowie XIX wieku, pozostali na początku XX wieku podali wiele interesujących rozwiązań.

Przyjrzyjmy się kilku przykładom. Znalezienie szczególnego rozwiązania dla małych  (dla
(dla 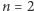 jest nim, na przykład,
jest nim, na przykład, 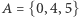 oraz
oraz 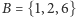 ) nie nastręcza większych kłopotów. Dla większych wykładników poziom trudności obliczeń wzrasta bardzo szybko, np. dla
) nie nastręcza większych kłopotów. Dla większych wykładników poziom trudności obliczeń wzrasta bardzo szybko, np. dla 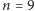 przykładowe rozwiązanie to
przykładowe rozwiązanie to

Polecam Czytelnikowi próbę znalezienia jakiegokolwiek rozwiązania dla 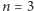 (przykładowe można znaleźć na końcu artykułu). Wydaje się, że problem Prouheta-Tarry'ego-Escotta jest trudny do rozwikłania, nawet jeśli postanowimy wspomóc się komputerem. Tymczasem czeka na nas ogromna niespodzianka. Okazuje się bowiem, że jesteśmy w stanie prosto skonstruować pewne rozwiązania dla dowolnej potęgi
(przykładowe można znaleźć na końcu artykułu). Wydaje się, że problem Prouheta-Tarry'ego-Escotta jest trudny do rozwikłania, nawet jeśli postanowimy wspomóc się komputerem. Tymczasem czeka na nas ogromna niespodzianka. Okazuje się bowiem, że jesteśmy w stanie prosto skonstruować pewne rozwiązania dla dowolnej potęgi 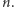 Ponadto żaden komputer nie będzie nam do tego potrzebny.
Ponadto żaden komputer nie będzie nam do tego potrzebny.
Zanim przedstawimy rozwiązanie, dla dowolnej liczby naturalnej  określmy rekurencyjnie pewne skończone ciągi zer i jedynek. Rozpoczniemy od definicji negatywu ciągu zero-jedynkowego, czyli zamianie każdego występującego w nim zera na jedynkę i odwrotnie. Negatyw ciągu
określmy rekurencyjnie pewne skończone ciągi zer i jedynek. Rozpoczniemy od definicji negatywu ciągu zero-jedynkowego, czyli zamianie każdego występującego w nim zera na jedynkę i odwrotnie. Negatyw ciągu 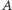 będziemy oznaczali przez
będziemy oznaczali przez 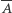 ; dla przykładu, jeżeli
; dla przykładu, jeżeli 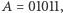 to
to 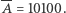 Niech teraz
Niech teraz 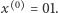 Gdy mamy już zdefiniowane
Gdy mamy już zdefiniowane 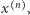 to przyjmujemy
to przyjmujemy 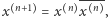 to znaczy do ciągu
to znaczy do ciągu 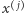 dopisujemy z prawej strony jego negatyw. Przykład:
dopisujemy z prawej strony jego negatyw. Przykład:

Tak zdefiniowane ciągi posłużą nam do rozwiązania problemu. Dla ustalonej liczby naturalnej 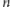 podzielimy teraz zbiór
podzielimy teraz zbiór 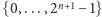 na takie dwa rozłączne zbiory, że odpowiednie sumy zgadzają się dla potęg od 0 do
na takie dwa rozłączne zbiory, że odpowiednie sumy zgadzają się dla potęg od 0 do 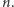 Niech
Niech

są to zatem numery tych wyrazów ciągu 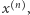 które są równe odpowiednio 0 lub 1. Wtedy
które są równe odpowiednio 0 lub 1. Wtedy 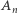 i
i 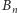 są poszukiwanymi zbiorami. Dowód będzie przebiegał indukcyjnie względem
są poszukiwanymi zbiorami. Dowód będzie przebiegał indukcyjnie względem  Dla
Dla 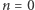 mamy
mamy

Wykonamy teraz krok indukcyjny. Załóżmy, że mamy już zdefiniowane 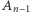 oraz
oraz  spełniające tezę. Niech
spełniające tezę. Niech
 |
Wtedy 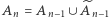 i analogicznie
i analogicznie 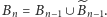 Równości te wynikają wprost z definicji ciągu
Równości te wynikają wprost z definicji ciągu 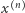 i są kluczową obserwacją wykorzystywaną w kroku indukcyjnym. Jeżeli teraz
i są kluczową obserwacją wykorzystywaną w kroku indukcyjnym. Jeżeli teraz 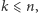 to, oznaczając przez
to, oznaczając przez 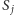 sumę
sumę 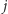 -tych potęg liczb ze zbioru
-tych potęg liczb ze zbioru 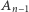 (dla
(dla 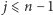 równą sumie
równą sumie 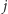 -tych potęg liczb ze zbioru
-tych potęg liczb ze zbioru 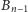 ), mamy:
), mamy:

Analogicznie moglibyśmy udowodnić tę samą równość dla sumy 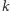 -tych potęg liczb ze zbioru
-tych potęg liczb ze zbioru 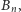 co kończy dowód indukcyjny.
co kończy dowód indukcyjny.
Zaprezentowana metoda ma jedną zaletę - pozwala w prosty sposób skonstruować jakiekolwiek rozwiązanie. Problemem jest jednak jej optymalność. Zwróćmy uwagę na to, że dla 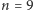 otrzymujemy w ten sposób zbiory
otrzymujemy w ten sposób zbiory 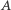 i
i 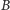 złożone z
złożone z 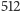 elementów każdy, a tymczasem widzieliśmy wcześniej rozwiązanie, w którym zbiory
elementów każdy, a tymczasem widzieliśmy wcześniej rozwiązanie, w którym zbiory 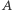 oraz
oraz 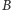 były "zaledwie" dziesięcioelementowe. Okazuje się, że rozwiązania dla wykładnika
były "zaledwie" dziesięcioelementowe. Okazuje się, że rozwiązania dla wykładnika  muszą być zbiorami złożonymi z co najmniej
muszą być zbiorami złożonymi z co najmniej 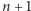 liczb całkowitych. Rozwiązanie, które spełnia to oszacowanie jako równość, nazywamy idealnym. Największym wykładnikiem, dla którego znane jest idealne rozwiązanie, jest
liczb całkowitych. Rozwiązanie, które spełnia to oszacowanie jako równość, nazywamy idealnym. Największym wykładnikiem, dla którego znane jest idealne rozwiązanie, jest 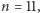 a jest nim para dwunastoelementowych zbiorów
a jest nim para dwunastoelementowych zbiorów

Ciągi skończone 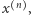 które posłużyły nam do konstrukcji rozwiązań, są początkowymi fragmentami pewnego nieskończonego ciągu zero-jedynkowego, zwanego ciągiem Thuego-Morse'a. Formalnie ciąg ten, oznaczany dalej przez
które posłużyły nam do konstrukcji rozwiązań, są początkowymi fragmentami pewnego nieskończonego ciągu zero-jedynkowego, zwanego ciągiem Thuego-Morse'a. Formalnie ciąg ten, oznaczany dalej przez 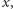 można zdefiniować jako
można zdefiniować jako 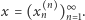 Jedną z ciekawych własności ciągu
Jedną z ciekawych własności ciągu  jest to, że nie zmienia się on pod wpływem operacji podstawień
jest to, że nie zmienia się on pod wpływem operacji podstawień 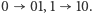 Wynika to z faktu, że wykonanie tej operacji na ciągu
Wynika to z faktu, że wykonanie tej operacji na ciągu 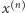 daje nam w rezultacie ciąg
daje nam w rezultacie ciąg  czego nietrudno dowieść za pomocą indukcji. Oczywiście, nie jest to jedyna jego interesująca cecha, jednak na zaprezentowanie wszystkich nie starczyłoby miejsca na marginesie tego artykułu, ani nawet w całym numerze Delty.
czego nietrudno dowieść za pomocą indukcji. Oczywiście, nie jest to jedyna jego interesująca cecha, jednak na zaprezentowanie wszystkich nie starczyłoby miejsca na marginesie tego artykułu, ani nawet w całym numerze Delty.