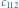Na tropie liczb gradowych
W matematycznym świecie od zawsze znajdowało się mnóstwo tajemnic czekających na odkrycie. Tak zawiłych i zdradzieckich, że tylko szaleńcy mogli w ogóle wyobrazić sobie ich istnienie. Tymi szaleńcami byli nieustraszeni matematycy, którzy już od stuleci (jeżeli nie tysiącleci) szukają, rozwiązują i wyjaśniają zagadki, które większość ludzi już dawno uznawała za beznadziejne przypadki (lub są one tak abstrakcyjne, że w żaden sposób nieosiągalne).

Mimo trudu i znoju wciąż pozostało mnóstwo do odkrycia. O istnieniu wielu przeszkód zapewne dopiero się dowiemy, lecz znane są takie, nad którymi zażarte prace, by je pokonać, wciąż trwają. Jednym z nich jest problem Collatza, zwany także problemem 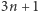 lub
lub 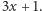 Sformułował go najprawdopodobniej niemiecki matematyk Lothar Collatz. Bierze się pod uwagę również kilku innych potencjalnych autorów, między innymi Bryana Thwaitesa, który ogłosił, że to on wpadł na ten problem około dwadzieścia lat przed jego opublikowaniem (czyli równolegle do Collatza). Czy mówił prawdę? Może to kolejna zagadka ukryta w naszym problemie? On sam zaś chowa się przed nami, zmieniając swoją nazwę. Zagadnienie jest znane również jako: problem Ulama, problem Kakutaniego, problem z Syracuse, problem Hasse'a oraz problem Thwaitesa. Zainteresowanie nim znacznie wzrosło, kiedy ustanowiono nagrodę dla wytrwałego poszukiwacza, który znajdzie rozwiązanie albo chociaż się do niego zbliży (bez precyzyjnego określenia, na czym owo zbliżenie ma polegać). Ta zachęta nie wyciągnęła jednak badaczy ze ślepego zaułka. Mimo starań wielu matematyków zagadnienie wciąż pozostało nierozstrzygnięte. Powstało nawet przekonanie, że problem musiał zostać stworzony przez matematycznych wrogów w celu odciągnięcia ich od naprawdę potrzebnych i ważnych spraw. Poszukiwania porzucił nawet jeden z najsłynniejszych matematyków Paul Erdős, określając zagadnienie słowami: "beznadziejne, absolutnie beznadziejne" oraz "być może matematyka nie jest jeszcze gotowa na takie problemy". Te słowa ostudziły zapał wielu poszukiwaczy, ale nie wszystkich, bo skoro matematyka nie jest jeszcze gotowa na takie problemy, to dlaczego by nie pomóc jej stać się gotową?
Sformułował go najprawdopodobniej niemiecki matematyk Lothar Collatz. Bierze się pod uwagę również kilku innych potencjalnych autorów, między innymi Bryana Thwaitesa, który ogłosił, że to on wpadł na ten problem około dwadzieścia lat przed jego opublikowaniem (czyli równolegle do Collatza). Czy mówił prawdę? Może to kolejna zagadka ukryta w naszym problemie? On sam zaś chowa się przed nami, zmieniając swoją nazwę. Zagadnienie jest znane również jako: problem Ulama, problem Kakutaniego, problem z Syracuse, problem Hasse'a oraz problem Thwaitesa. Zainteresowanie nim znacznie wzrosło, kiedy ustanowiono nagrodę dla wytrwałego poszukiwacza, który znajdzie rozwiązanie albo chociaż się do niego zbliży (bez precyzyjnego określenia, na czym owo zbliżenie ma polegać). Ta zachęta nie wyciągnęła jednak badaczy ze ślepego zaułka. Mimo starań wielu matematyków zagadnienie wciąż pozostało nierozstrzygnięte. Powstało nawet przekonanie, że problem musiał zostać stworzony przez matematycznych wrogów w celu odciągnięcia ich od naprawdę potrzebnych i ważnych spraw. Poszukiwania porzucił nawet jeden z najsłynniejszych matematyków Paul Erdős, określając zagadnienie słowami: "beznadziejne, absolutnie beznadziejne" oraz "być może matematyka nie jest jeszcze gotowa na takie problemy". Te słowa ostudziły zapał wielu poszukiwaczy, ale nie wszystkich, bo skoro matematyka nie jest jeszcze gotowa na takie problemy, to dlaczego by nie pomóc jej stać się gotową?
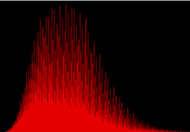
Rys. 1 Ilustracja ciągu Collatza dla  ; pierwszy wyraz równy 1 to
; pierwszy wyraz równy 1 to 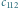
Problem jest dość prosto sformułowany, a mianowicie dotyczy ciągu tworzonego według rekurencyjnej zasady:

gdzie 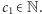 Po wybraniu kilku przykładowych pierwszych wyrazów otrzymujemy poniższe ciągi:
Po wybraniu kilku przykładowych pierwszych wyrazów otrzymujemy poniższe ciągi:

Każdy z powyższych ciągów wpada w pętlę 4, 2, 1, 4, 2, 1 … Wiadomo już, że wszystkie ciągi o wyrazie początkowym mniejszym niż 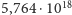 kończą się tą właśnie sekwencją. Meritum problemu polega na tym, że nie jest znany żaden dowód na to, że ta pętla będzie kończyła ciąg dla każdej liczby początkowej.
kończą się tą właśnie sekwencją. Meritum problemu polega na tym, że nie jest znany żaden dowód na to, że ta pętla będzie kończyła ciąg dla każdej liczby początkowej.
Na rysunku 1 można zaobserwować naturę ciągu, od której wzięła się nazwa liczby gradowe. Chodzi o podobieństwo zachowania się liczb w ciągu do kryształków lodu podróżujących w chmurze gradowej. Kawałki lodu wędrują z góry na dół i z powrotem niesione przez burzliwe wiatry, zbierając przy tym masę. W końcu przekracza ona poziom krytyczny, siła wiatru przegrywa z grawitacją i kryształki lodu spadają na ziemię w postaci gradu. Jak widzimy, podobnie dzieje się z wyrazami ciągu, które rosną, maleją, rosną, aż ostatecznie spadają do jedynki.
Matematycy próbowali już na najróżniejsze sposoby odnaleźć rozwiązanie. Podążali wieloma drogami, szlakami i tropami. Niestety, większość zawędrowała w ślepą uliczkę, pozostawiając problem bez odpowiedzi. Ciekawą rzeczą, mogącą przybliżyć do rozwiązania, jest poznanie podstawowych własności ciągu, na przykład zależności jego wartości maksymalnej od jego wartości początkowej.
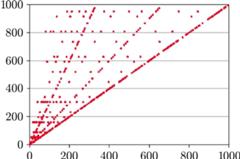
Rys. 2 Wartości maksymalne ciągów dla pierwszych wyrazów mniejszych od 1000
Maksima układają się wzdłuż linii poziomych i skośnych. Linie poziome biorą się stąd, że maksima lubią się powtarzać. Na przykład ciąg 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 ma maksimum 52. Nie jest to maksimum tylko dla liczby początkowej 7, ale także dla liczb 22, 11, 34, 17, 52. Kto wie, może dla każdego maksimum da się przydzielić choćby jedną linię skośną (to znaczy taką, na której znajdują się maksima nieskończenie wielu ciągów) czy poziomą (maksimum wystarczająco wielu ciągów)?
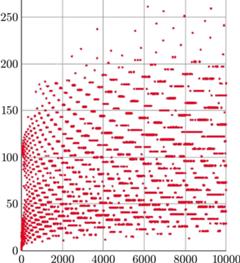
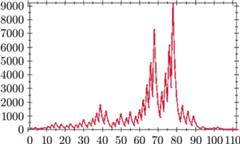
Rys. 3 Długości ciągów dla wyrazów początkowych mniejszych niż 10 000 (sama liczba początkowa nie została wliczona do długości)
Kolejną własnością są długości ciągu (aż do pojawienia się w ciągu wartości 1). Mimo braku uporządkowania (w każdym razie na pierwszy rzut oka), inaczej niż w przypadku wartości maksymalnych, można odczytać choćby kilka własności. Jedną z takich ciekawostek są rekordziści. Na przykład: najmniejszą liczbą początkową tworzącą ciąg o długości przekraczającej sto jest 27 (długość to 112), liczbą początkową dającą największą długość ciągu w przedziale od 1 do 100 jest 97 (długość 119), w przedziale od 1 do 100000 liczba 77031 (351), zaś w przedziale od 1 do 1 000 000 liczba 837799 (525). Można szukać takich ciągów, dla których długość ciągu przekracza wartość początkową. W ciągu występują też ciekawe powtórzenia, na przykład w przedziale od 1 do 100 występuje aż 6 trzyelementowych zbiorów kolejnych liczb początkowych dających taką samą długość. Są to {28, 29, 30} (19), {36, 37, 38} (22), {44, 45, 46} (17), {49, 50, 51} (25), {65, 66, 67} (28) oraz {68, 69, 70} (15). Jeśli prześledzić ciągi o wartości początkowej do 102, zobaczymy pierwszy taki zbiór pięcioelementowy {98, 99, 100, 101, 102} (26). Kolejnym zbiorem pięcioelementowym jest {130, 131, 132, 133, 134} (29). W danej funkcji można także znaleźć wiele innych powtórzeń: czteroelementowe {314, 315, 316, 317} (38), sześcioelementowe {386, 387, 388, 389, 390, 391} (121). Wśród liczb mniejszych od 10 000 000 można znaleźć 65 kolejnych liczb początkowych dających taką samą długość ciągu. Są to {5772712, 5772713, …, 5772776} (215) oraz {9170858, 9170859, …, 9170922} (226).
Pozostają pytania: po co zajmować się takimi problemami? Dlaczego nasi poszukiwacze tak chcą odnaleźć rozwiązanie? Już wiele razy w historii zdarzało się, że matematycy zajmowali się jakimś zagadnieniem z czystej ciekawości, bez praktycznego celu, a dopiero po latach znajdowano dla niego zastosowanie. Stało się tak, między innymi, z liczbami pierwszymi. Choć są też takie obszary matematyki, które jak na razie zastosowań dla siebie nie znalazły (i raczej się na to nie zapowiada). Innym powodem szukania rozwiązania jest to, że błądzenie po ciemku zmusza matematyków do wysiłku, do treningu i rozwoju, a w konsekwencji do rozwoju całej matematyki, ponieważ w trakcie takich poszukiwań powstają nowe podejścia i narzędzia, które mogą być użyte w zupełnie innych obszarach. Właśnie dlatego takie poszukiwania warto prowadzić. To kolejne naukowe zagadnienie, w którym na początku prac trzeba zadać sobie pytanie, nie "Co my z nim zrobimy?", ale "Co ono zrobi z nami?". Dlatego jeszcze raz szczerze zachęcam do rozpoczęcia własnych poszukiwań.
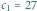 ; pierwszy wyraz równy 1 to
; pierwszy wyraz równy 1 to