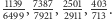Mała Delta
Sposób na niesforne ulamki
- Z tymi ułamkami to zupełnie nic nie wiadomo - narzekał po lekcji matematyki Janek. - Na przyklad 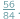

Wyglada nieladnie, w liczniku i w mianowniku straszą takie duże liczby, ale jak się dobrze przyjrzeć i poskracać: przez 2, jeszcze raz przez 2, przez 7..., robi się z niego całkiem miły ułamek, zwyczajne 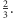 Ułamek z małymi liczbami w liczniku i w mianowniku bardzo łatwo "rozdmuchać". Na przykład
Ułamek z małymi liczbami w liczniku i w mianowniku bardzo łatwo "rozdmuchać". Na przykład 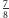 można rozszerzyć do
można rozszerzyć do 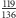 mnożąc licznik i mianownik przez 17. Ale bądź taki mądry i skróć olbrzyma, żeby się zrobił przyjemny i zgrabny. Skąd mam wiedzieć, że trzeba licznik i mianownik podzielić przez 17? O mam tutaj taki okropny ułamek
mnożąc licznik i mianownik przez 17. Ale bądź taki mądry i skróć olbrzyma, żeby się zrobił przyjemny i zgrabny. Skąd mam wiedzieć, że trzeba licznik i mianownik podzielić przez 17? O mam tutaj taki okropny ułamek 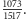 Od godziny próbuję go skrócić i wciąż nie wiem, czy się da, czy nie.
Od godziny próbuję go skrócić i wciąż nie wiem, czy się da, czy nie.
- A ja mam sposób na twoje ułamki - pocieszał Janka Andrzej. - Zabierzemy się do nich zupełnie inaczej, nie będziemy na oślep szukali, przez co można by skrócić. Zastanów się na przykład, czy można skrócić ułamek 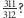
- Chyba nie... Tak mi się wydaje, że nie.
- A dlaczego tak ci się wydaje?
- No, bo między licznikiem i mianownikiem jest bardzo mała różnica, tylko 1 - niepewnie powiedział Janek.
- Bardzo słusznie. Zwróciłeś uwagę na ważny fakt:
Fakt. Jeżeli jakieś dwie liczby dzielą się przez wspólny dzielnik 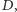 to ich różnica też musi się dzielić przez
to ich różnica też musi się dzielić przez 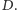
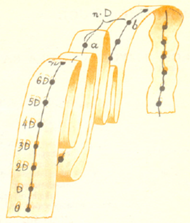
Widać to dobrze na osi liczbowej.
Dużymi kropkami oznaczyliśmy liczby podzielne przez 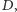 a wiec
a wiec 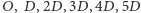 itd. Rysunek pokazuje, że różnica dwóch takich liczb też dzieli się przez
itd. Rysunek pokazuje, że różnica dwóch takich liczb też dzieli się przez 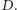
Uzasadnić możemy to w ten sposób: jeśli liczba a dzieli się przez  to
to 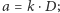 jeśli liczba
jeśli liczba  dzieli się przez
dzieli się przez 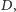 to
to 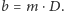 Wobec tego
Wobec tego 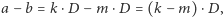 a to oznacza, że
a to oznacza, że 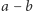 też dzieli się przez
też dzieli się przez 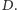
Moglibyśmy nawet udowodnić takie twierdzenie:
Twierdzenie. Liczby 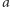 oraz
oraz 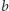 maja taki sam największy wspólny dzielnik, co liczby
maja taki sam największy wspólny dzielnik, co liczby 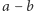 oraz
oraz 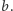
Skorzystamy z tego twierdzenia, żeby skrócić ułamek 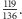 Obliczmy różnicę
Obliczmy różnicę 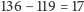 i zamiast szukać największego wspólnego dzielnika dla liczb 119 i 136 poszukamy go dla liczb 17 i 119. Nietrudno się domyśleć, że jest 17. Rzeczywiscie, po podzieleniu otrzymamy
i zamiast szukać największego wspólnego dzielnika dla liczb 119 i 136 poszukamy go dla liczb 17 i 119. Nietrudno się domyśleć, że jest 17. Rzeczywiscie, po podzieleniu otrzymamy 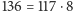 i
i 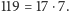
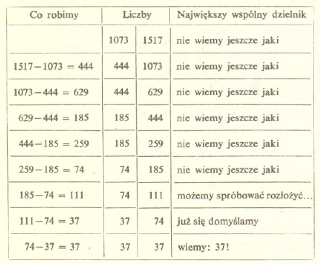
Mamy wiec sposób na znalezienie największego wspólnego dzielnika liczb 1517 i 1073. Trochę liczenia i uprościmy twój okropny ułamek. Nie powinno nam to zając nawet pięciu minut.
Obliczenia i ich wyniki zapisywać będziemy po kolei w tabelce. W każdym następnym wierszu tabelki (tam, gdzie napisaliśmy "liczby") zamiast liczb z poprzedniego wiersza wpisywać będziemy inne dwie liczby: mniejszą z liczb, które były wyżej, oraz ich różnicę. Liczby będą się zmieniały, ale ich wspólny dzielnik będzie ten sam. Podziel teraz licznik i mianownik przez 37 (bądź spokojny, na pewno da się podzielić) i skróć ułamek, nad którym się tak długo męczyłeś.
Jeśli macie ochotę - drodzy Czytelnicy - to skróćcie ułamek Janka. Cierpliwi mogą się przekonać, że wszystkie liczby napisane w tabelce przez Andrzeja dzielą się przez 37.
Sprawdźmy jeszcze, co się stanie, gdy weźmiemy do obliczeń ułamek nieskracalny, na przykład 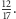 Obliczenia zanotujemy, jak poprzednio, w odpowiedniej tabelce:
Obliczenia zanotujemy, jak poprzednio, w odpowiedniej tabelce:
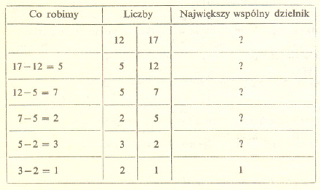
Okazuje się, ze największą i jedyną liczbą, przez którą się dzielą i 12, i 17, jest 1. Nie można więc skrócić ułamka 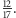 Jest on nieskracalny.
Jest on nieskracalny.
Dla wszystkich, którzy chcieliby sprawdzić nową metodę skracania ułamków, przygotowaliśmy przykłady takich specjalnych "olbrzymów". Przekonajcie się, że zwykłą metodą nie łatwo będzie je skrócić: