Reszta jest dziełem człowieka, czyli Fermat i inni
Nie ma słynniejszego twierdzenia niż Wielkie Twierdzenie Fermata (WTwF) i tego nie zamierzam tu dowodzić. Zacznę po prostu od sformułowania faktu, który od 1995 roku jest rzeczywiście twierdzeniem za sprawą Andrew Wilesa, a wcześniej przez około trzy i pół wieku był hipotezą zajmującą głowy największych matematyków i rzesze amatorów...

Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.
Twierdzenie 1. Jeżeli  jest liczbą naturalną większą od
jest liczbą naturalną większą od 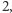 to równanie
to równanie

nie ma rozwiązań w liczbach naturalnych 
Jak powszechnie wiadomo, wykładnik 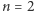 jest zupełnie wyjątkowy, gdyż wtedy równanie (1), zwane równaniem Pitagorasa, ma nieskończenie wiele nieproporcjonalnych rozwiązań, a nawet dużo więcej - ma rozwiązanie w wielomianach o współczynnikach całkowitych:
jest zupełnie wyjątkowy, gdyż wtedy równanie (1), zwane równaniem Pitagorasa, ma nieskończenie wiele nieproporcjonalnych rozwiązań, a nawet dużo więcej - ma rozwiązanie w wielomianach o współczynnikach całkowitych:

Pokażemy przede wszystkim, że dla ustalonego 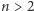 równanie (1) nie ma rozwiązań w wielomianach
równanie (1) nie ma rozwiązań w wielomianach 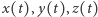 o współczynnikach zespolonych, chyba że wszystkie wymienione wielomiany są stałe! Załóżmy nie wprost, że trójka wielomianów
o współczynnikach zespolonych, chyba że wszystkie wymienione wielomiany są stałe! Załóżmy nie wprost, że trójka wielomianów 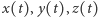 jest hipotetycznym rozwiązaniem równania (1), przy czym nie wszystkie wielomiany
jest hipotetycznym rozwiązaniem równania (1), przy czym nie wszystkie wielomiany  są stałe oraz (co możemy założyć)
są stałe oraz (co możemy założyć) 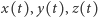 nie mają wspólnego dzielnika wielomianowego dodatniego stopnia. Jeśli
nie mają wspólnego dzielnika wielomianowego dodatniego stopnia. Jeśli 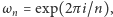 to mamy tożsamość algebraiczną
to mamy tożsamość algebraiczną

z której po podstawieniu  i pomnożeniu obu stron przez
i pomnożeniu obu stron przez 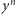 otrzymujemy
otrzymujemy

Nasze hipotetyczne wielomiany spełniają więc równanie

Ponieważ czynniki po prawej stronie są parami względnie pierwsze, więc z jednoznaczności rozkładu wielomianów na czynniki wynika, że istnieją takie wielomiany 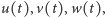 że
że

Po rozwiązaniu pierwszych dwóch z powyższych równań względem 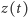 oraz
oraz 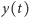 i podstawieniu tych wartości do trzeciego równania otrzymujemy po uproszczeniach
i podstawieniu tych wartości do trzeciego równania otrzymujemy po uproszczeniach

Ponieważ z liczb zespolonych można wyciągać pierwiastki dowolnych stopni, więc powyższą równość można zapisać jako

gdzie największy ze stopni wielomianów 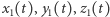 jest
jest  razy mniejszy niż największy ze stopni wielomianów
razy mniejszy niż największy ze stopni wielomianów  To postępowanie można kontynuować, ale to oczywista sprzeczność! Przeprowadzone rozumowanie ilustruje słynną metodę regresji: za pomocą hipotetycznego rozwiązania konstruujemy rozwiązanie w pewnym sensie mniejsze i to prowadzi do sprzeczności. W rozważonym przykładzie mielibyśmy nieskończony ciąg wielomianów o ściśle malejących dodatnich stopniach! Metodę tę stosowano z pewnym powodzeniem również do przypadku liczbowego, chociaż pojawiają się tu już dość szybko fundamentalne trudności i, jak pokazała historia, nie udało się ich do końca przezwyciężyć.
To postępowanie można kontynuować, ale to oczywista sprzeczność! Przeprowadzone rozumowanie ilustruje słynną metodę regresji: za pomocą hipotetycznego rozwiązania konstruujemy rozwiązanie w pewnym sensie mniejsze i to prowadzi do sprzeczności. W rozważonym przykładzie mielibyśmy nieskończony ciąg wielomianów o ściśle malejących dodatnich stopniach! Metodę tę stosowano z pewnym powodzeniem również do przypadku liczbowego, chociaż pojawiają się tu już dość szybko fundamentalne trudności i, jak pokazała historia, nie udało się ich do końca przezwyciężyć.
Wielkie sukcesy uzyskał jednak Ernst Eduard Kummer w połowie XIX wieku. Rozważał on mianowicie pierścień 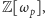 gdzie
gdzie  jest rozważanym wykładnikiem i zakłada się, że
jest rozważanym wykładnikiem i zakłada się, że 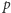 jest liczbą pierwszą nieparzystą. Do pierścienia
jest liczbą pierwszą nieparzystą. Do pierścienia 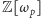 należą liczby zespolone postaci
należą liczby zespolone postaci 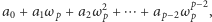 gdzie
gdzie  to zwykłe liczby całkowite. W przypadku, gdy w pierścieniu
to zwykłe liczby całkowite. W przypadku, gdy w pierścieniu 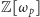 rozkład na czynniki nierozkładalne jest jednoznaczny, nierozwiązalność równania (1) można uzyskać w podobny sposób jak wyżej dla wielomianów. Pewne komplikacje związane ze skutecznym przeprowadzeniem regresji związane są z istnieniem w pierścieniu
rozkład na czynniki nierozkładalne jest jednoznaczny, nierozwiązalność równania (1) można uzyskać w podobny sposób jak wyżej dla wielomianów. Pewne komplikacje związane ze skutecznym przeprowadzeniem regresji związane są z istnieniem w pierścieniu  nietrywialnych elementów odwracalnych, tzn. takich elementów
nietrywialnych elementów odwracalnych, tzn. takich elementów 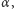 że
że 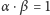 dla pewnego
dla pewnego 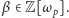 Za trywialne uznajemy elementy postaci
Za trywialne uznajemy elementy postaci 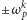 ; oczywiście są one odwracalne. Dla
; oczywiście są one odwracalne. Dla 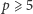 istnieją również elementy odwracalne
istnieją również elementy odwracalne 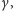 które nie są pierwiastkami z jedności. Na przykład dla
które nie są pierwiastkami z jedności. Na przykład dla  przyjmijmy
przyjmijmy  Mamy wówczas
Mamy wówczas

a więc 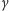 jest odwracalny i, co łatwo wykazać, nietrywialny. Niestety, dla
jest odwracalny i, co łatwo wykazać, nietrywialny. Niestety, dla 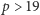 w pierścieniu
w pierścieniu 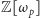 nie ma jednoznaczności rozkładu na elementy nierozkładalne, a oto przykład dla
nie ma jednoznaczności rozkładu na elementy nierozkładalne, a oto przykład dla 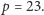 Niech
Niech 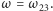 Mamy
Mamy

Zatem liczba 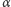 dzieli się przez
dzieli się przez  mimo tego, że
mimo tego, że 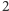 nie dzieli żadnego z czynników poprzedniego iloczynu. Ponadto można wykazać, że liczba
nie dzieli żadnego z czynników poprzedniego iloczynu. Ponadto można wykazać, że liczba  jest nierozkładalna w
jest nierozkładalna w 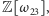 a więc w
a więc w  nie ma jednoznaczności rozkładu na czynniki nierozkładalne! Brak jednoznaczności rozkładu na czynniki to największa trudność, którą należy pokonać, adaptując metodę regresji. Genialny pomysł Kummera polegał na wprowadzeniu do rozważań nowych obiektów, tzw. liczb idealnych i wykazaniu, że każda liczba z
nie ma jednoznaczności rozkładu na czynniki nierozkładalne! Brak jednoznaczności rozkładu na czynniki to największa trudność, którą należy pokonać, adaptując metodę regresji. Genialny pomysł Kummera polegał na wprowadzeniu do rozważań nowych obiektów, tzw. liczb idealnych i wykazaniu, że każda liczba z 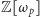 rozkłada się w jednoznaczny sposób na iloczyn liczb idealnych. Używając współczesnego języka (wprowadzonego przez Dedekinda), zbiory liczb z
rozkłada się w jednoznaczny sposób na iloczyn liczb idealnych. Używając współczesnego języka (wprowadzonego przez Dedekinda), zbiory liczb z 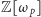 podzielnych przez daną liczbę idealną Kummera to po prostu ideały pierwsze pierścienia
podzielnych przez daną liczbę idealną Kummera to po prostu ideały pierwsze pierścienia 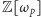 - stąd zresztą ich nazwa! Miarą niejednoznaczności rozkładu na poziomie liczb jest tzw. grupa klas ideałów pierścienia
- stąd zresztą ich nazwa! Miarą niejednoznaczności rozkładu na poziomie liczb jest tzw. grupa klas ideałów pierścienia  której definicji tu nie podamy. Nadmienimy tylko, że Kummer udowodnił, między innymi, następujące twierdzenie.
której definicji tu nie podamy. Nadmienimy tylko, że Kummer udowodnił, między innymi, następujące twierdzenie.
Twierdzenie 2. Jeżeli 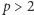 jest liczbą pierwszą oraz rząd grupy klas ideałów nie dzieli się przez
jest liczbą pierwszą oraz rząd grupy klas ideałów nie dzieli się przez 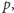 to równanie (1) nie ma rozwiązań dla wykładnika
to równanie (1) nie ma rozwiązań dla wykładnika 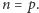
Metody wypracowane przez Kummera, Dedekinda i innych dały początek algebraicznej teorii liczb, ważnemu działowi matematyki współczesnej. Grupa klas ideałów i grupa elementów odwracalnych są bardzo blisko spokrewnione z funktorami 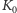 oraz
oraz 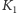 algebraicznej K-teorii - nowoczesnego działu współczesnej matematyki, który próbuje łączyć algebrę i geometrię na wysokim i abstrakcyjnym poziomie.
algebraicznej K-teorii - nowoczesnego działu współczesnej matematyki, który próbuje łączyć algebrę i geometrię na wysokim i abstrakcyjnym poziomie.

Trzeba zmierzać do końca tej historii i dlatego muszę przemilczeć wiele ciekawych częściowych rezultatów uzyskanych przed rokiem 1983. W tymże roku Gerd Faltings udowodnił hipotezę Mordella o tym, że na każdej krzywej rodzaju większego od 1 istnieje co najwyżej skończenie wiele punktów wymiernych. Wynika stąd, że dla 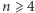 równanie (1) ma co najwyżej skończenie wiele nieproporcjonalnych rozwiązań.
równanie (1) ma co najwyżej skończenie wiele nieproporcjonalnych rozwiązań.
To oczywiście wspaniały wynik, ale przecież nie tego oczekiwał Fermat. Na szczęście historia nabrała tempa, gdy w 1986 roku Gerhard Frey związał z hipotetycznym rozwiązaniem równania (1) 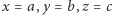 następującą krzywą eliptyczną
następującą krzywą eliptyczną

Wyróżnik tej krzywej wynosi 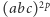 i to nasunęło Freyowi przypuszczenie, że taka krzywa
i to nasunęło Freyowi przypuszczenie, że taka krzywa  w ogóle nie powinna istnieć - to oczywiście zakończyłoby dowód WTwF! Pomysł okazał się trafiony, ale szczegóły dopinało wielu wybitnych matematyków. I tak Jean-Pierre Serre sformułował precyzyjnie przypuszczenie Freya, a Ken Ribet wyprowadził je w tym samym roku ze słynnej hipotezy Taniyamy-Shimury-Weila o tym, że każda krzywa eliptyczna o współczynnikach wymiernych jest modularna. Tę właśnie hipotezę udowodnił Andrew Wiles w 1995 roku z pomocą swojego ucznia Richarda Taylora dla tzw. krzywych półstabilnych - klasa tych krzywych obejmuje krzywe typu Freya i to
w ogóle nie powinna istnieć - to oczywiście zakończyłoby dowód WTwF! Pomysł okazał się trafiony, ale szczegóły dopinało wielu wybitnych matematyków. I tak Jean-Pierre Serre sformułował precyzyjnie przypuszczenie Freya, a Ken Ribet wyprowadził je w tym samym roku ze słynnej hipotezy Taniyamy-Shimury-Weila o tym, że każda krzywa eliptyczna o współczynnikach wymiernych jest modularna. Tę właśnie hipotezę udowodnił Andrew Wiles w 1995 roku z pomocą swojego ucznia Richarda Taylora dla tzw. krzywych półstabilnych - klasa tych krzywych obejmuje krzywe typu Freya i to  kończy dowód WTwF. Artykuł zakończymy omówieniem pojęcia krzywa eliptyczna modularna. Jest wiele sformułowań tej własności - wybieramy wersję arytmetyczną. Z każdą krzywą eliptyczną
kończy dowód WTwF. Artykuł zakończymy omówieniem pojęcia krzywa eliptyczna modularna. Jest wiele sformułowań tej własności - wybieramy wersję arytmetyczną. Z każdą krzywą eliptyczną

i liczbą pierwszą 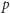 można związać kongruencję
można związać kongruencję

Niech 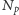 oznacza liczbę rozwiązań tej kongruencji modulo
oznacza liczbę rozwiązań tej kongruencji modulo 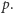 Helmut Hasse udowodnił w 1933 roku hipotezę Artina głoszącą, że
Helmut Hasse udowodnił w 1933 roku hipotezę Artina głoszącą, że

Wynika z niej natychmiast, że rozwiązania kongruencji istnieją dla dostatecznie dużych 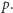 Jest to satysfakcjonujący rezultat ilościowy, ale być może o liczbie
Jest to satysfakcjonujący rezultat ilościowy, ale być może o liczbie  można powiedzieć coś więcej, niż tylko to, że jest mniejsza od
można powiedzieć coś więcej, niż tylko to, że jest mniejsza od 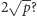 Okazuje się, że tak! Przyjrzyjmy się najpierw krzywej
Okazuje się, że tak! Przyjrzyjmy się najpierw krzywej

Bardzo łatwo wykazać, że jeśli 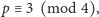 to
to  Dużo trudniej zauważyć, że dla
Dużo trudniej zauważyć, że dla 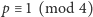 też istnieje dość zwarty i dość jednolity wzór na liczbę
też istnieje dość zwarty i dość jednolity wzór na liczbę 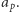 Mianowicie liczbę
Mianowicie liczbę 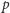 przedstawiamy w postaci
przedstawiamy w postaci 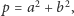 gdzie
gdzie 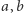 są dodatnie, przy czym
są dodatnie, przy czym 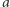 jest nieparzysta (
jest nieparzysta ( 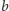 zaś parzysta). Jak wiadomo, takie przedstawienie liczby pierwszej
zaś parzysta). Jak wiadomo, takie przedstawienie liczby pierwszej 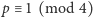 zawsze istnieje i jest dokładnie jedno - jest to twierdzenie Fermata (ani małe, ani wielkie, ale wspaniałe). Wówczas
zawsze istnieje i jest dokładnie jedno - jest to twierdzenie Fermata (ani małe, ani wielkie, ale wspaniałe). Wówczas 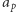 dane jest następującym wzorem
dane jest następującym wzorem

Krzywa eliptyczna 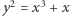 należy do dość wąskiej klasy krzywych eliptycznych z mnożeniem zespolonym - odwzorowanie
należy do dość wąskiej klasy krzywych eliptycznych z mnożeniem zespolonym - odwzorowanie 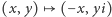 przeprowadza punkty krzywej na punkty krzywej. Niewiele krzywych ma tego typu algebraiczne "symetrie".
przeprowadza punkty krzywej na punkty krzywej. Niewiele krzywych ma tego typu algebraiczne "symetrie".
Rozpatrzmy teraz typową krzywą eliptyczną (bez mnożenia zespolonego)

oraz, jak wyżej, odpowiednie kongruencje modulo różne liczby pierwsze 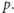 Okazuje się, że ciąg liczb
Okazuje się, że ciąg liczb 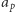 można uzyskać w następujący sposób. Rozważmy iloczyn funkcyjny
można uzyskać w następujący sposób. Rozważmy iloczyn funkcyjny

przy czym dla uproszczenia pomińmy kwestię zbieżności. Jeśli zapiszemy teraz powyższy iloczyn formalny jako szereg formalny

to okazuje się, że dla każdej liczby pierwszej 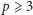 zachodzi równość
zachodzi równość 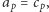 a więc znowu otrzymaliśmy "wzór" na
a więc znowu otrzymaliśmy "wzór" na 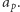 Hipoteza Taniyamy-Shimury-Weila przewidywała właśnie, że tego typu "wzór" na
Hipoteza Taniyamy-Shimury-Weila przewidywała właśnie, że tego typu "wzór" na 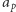 można podać dla każdej krzywej eliptycznej o współczynnikach wymiernych. Znaczenie twierdzenia o modularności znacznie wykracza poza zastosowanie do dowodu WTwF. Daje ono, na przykład, fundament do ścisłego sformułowania hipotezy Bircha-Swinnertona-Dyera, która nadal jest jednym z problemów milenijnych. Do tych zastosowań trzeba przywołać sformułowania bardziej geometryczno-analityczne od stosowanych w tym tekście.
można podać dla każdej krzywej eliptycznej o współczynnikach wymiernych. Znaczenie twierdzenia o modularności znacznie wykracza poza zastosowanie do dowodu WTwF. Daje ono, na przykład, fundament do ścisłego sformułowania hipotezy Bircha-Swinnertona-Dyera, która nadal jest jednym z problemów milenijnych. Do tych zastosowań trzeba przywołać sformułowania bardziej geometryczno-analityczne od stosowanych w tym tekście.
Na koniec odnieśmy się do słynnej myśli wypowiedzianej przez Leopolda Kroneckera, że liczby całkowite stworzył Bóg, a reszta jest dziełem człowieka. Historia WTwF doskonale ilustruje starą prawdę, że jeśli chcemy się czegoś dowiedzieć (pozornie prostego!) o bardzo prostych obiektach, musimy wyjść ze świata tychże obiektów i mieć nadzieję, że wzbogacona w ten sposób perspektywa pozwoli nam dostrzec te powiązania, które nie były widoczne z bliska. Do lat osiemdziesiątych XX wieku to wyjście z raju liczb naturalnych było bardzo ograniczone - cały czas obracano się w świecie liczb algebraicznych i ich rozkładów na czynniki. Pomysł Freya wyrwał badaczy WTwF z zaklętego kręgu liczb, a świat krzywych eliptycznych i form modularnych okazał się wystarczającym wzbogaceniem ubogiego i jakże błahego kontekstu WTwF.