Doświadcza wielu sytuacji wywołujących śmiech. Zna osoby, w towarzystwie których chętniej się śmieje. Rodzina, przyjaciele, koleżanki i koledzy - każdy z nich może być potencjalnym źródłem uśmiechu, zamieniając nasz smutek w radość. Nasza ulubiona komedia, ulubiony skecz kabaretowy potrafią nas rozbawić do łez. Wielokrotnie sposób, w jaki się śmiejemy, wywołuje śmiech u innych. Gdy przeglądamy stare gazety, czasem natrafiamy na dowcipy. Komiksy czytane w czasach dzieciństwa niejednokrotnie nas bawiły (niektórych zapewne dalej bawią). Czasem pojawiają się sytuacje okolicznościowe, tak niepowtarzalne, że już nigdy nie będą nas bawić tak dobrze, jak to robiły za pierwszym razem.

Wszystkie wymienione sytuacje łączy jedno słowo - wesoły. Matematyka długo pozostawała w cieniu i nie miała swoich "wesołych" pojęć. Sytuacja uległa znaczącej zmianie w 1994 roku, gdy Richard K. Guy w książce Unsolved Problems in Number Theory zdefiniował liczby wesołe oraz postawił liczne problemy dotyczące tychże liczb.

Nazwa ta jest o tyle intrygująca, że w pierwszej kolejności kojarzy nam się z liczbami, obiektami matematycznymi, które z natury swojej nazwy powinny być w jakiś sposób wesołe, radosne, może nawet zabawne. Ta subiektywna intuicja musi jednak pozostać w tyle, gdyż jak się za chwilę okaże, jest ona nietrafiona.

Czym więc są liczby wesołe? Wybierzmy liczbę naturalną 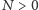i rozważmy następujący algorytm.

(1)

Oblicz sumę kwadratów cyfr wchodzących w skład zapisu liczby 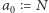i oznacz ją przez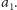

(2)

Jeżeli 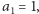zakończ algorytm. Jeżeli 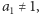przejdź do następnego kroku.

(3)

Mając już 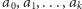dla pewnego 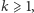zastosuj krok pierwszy do liczby 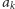- otrzymasz liczbę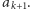

(4)

Jeżeli 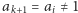dla pewnego 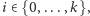zakończ algorytm. W przeciwnym przypadku kontynuuj algorytm, przechodząc do kroku (2), który stosujesz dla liczby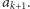

Jeżeli w kroku (2) dla pewnego 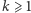zachodzi 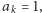to liczbę 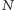nazwiemy wesołą. Jeżeli prawdziwy jest warunek 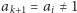dla pewnego 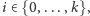to liczbę 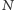nazwiemy smutną. W celu lepszego zrozumienia postawionej wyżej definicji przyjrzyjmy się kilku przykładom.

Weźmy liczbę 133. Krok (1) mówi nam "oblicz sumę kwadratów cyfr". W naszym przypadku jest to 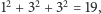a więc liczba różna od 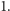Warunek z kroku (2) nie jest spełniony, przechodzimy więc do kroku (3). Zgodnie z krokiem (3) obliczamy teraz sumę kwadratów cyfr liczby 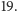Otrzymujemy 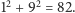Przechodząc do kroku (4), stwierdzamy, że warunek nie jest spełniony, a więc należy wrócić do kroku (2). Wykonując algorytm, otrzymujemy kolejno 68, 100, 1. Ostatecznie po pięciu powtórzeniach otrzymaliśmy jedynkę, co oznacza, że liczba 133 jest wesoła.

Niech teraz 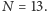Nie bez powodu wybraliśmy tę liczbę. Jest ona powszechnie uważana za liczbę pechową, co więcej, wiele osób często wstydzi się związku własnej osoby z liczbą 13. W niektórych hotelach nie ma oficjalnie trzynastego piętra - jeżeli numery pokojów rozpoczynają się od numeru piętra, to może się okazać, że po ułożeniu wszystkich numerów w porządku rosnącym po 1266 nastąpi 1400. Na niektórych konkursach na miss/mistera nie odnajdziemy uczestnika noszącego numer 13. Czy jednak te wszystkie obawy wobec liczby 13 są zawsze w pełni uzasadnione?

Sprawdźmy, czy 13 jest wesoła, a więc z naszego punktu widzenia ciekawa. Po kroku (1) otrzymujemy 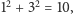a po powtórzeniu operacji sumowania kwadratów cyfr dostajemy 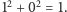Okazało się, że 13 jest liczbą wesołą! Odnaleźliśmy więc pozytywny aspekt tej liczby.

Każdy z nas może wreszcie przestać wstydzić się związku z nią, gdyż niezależnie od tego, jak źle różnym osobom może się kojarzyć nasz numer mieszkania, dzień miesiąca, w którym się urodziliśmy czy też numer z dziennika szkolnego, możemy im powiedzieć "Hej, moja liczba jest wesoła!" i z dumą wytłumaczyć zainteresowanym tę własność.

Dwa przykłady zaprezentowane powyżej dawały wynik pozytywny - liczby w kilku krokach redukowały się do jedynki. Przyjrzyjmy się teraz odmiennemu przypadkowi - weźmy niegroźnie wyglądającą liczbę 4. Wykonując algorytm, szybko okaże się, że jedynki nie osiągniemy. Mianowicie, dostaniemy kolejno 16, 37, 58, 89, 145, 42, 20, 4. Dalej nie musimy już liczyć, gdyż otrzymaliśmy liczbę, która wcześniej wystąpiła w procesie sprawdzania wesołości naszej liczby. To zapętlanie oznacza, że nie otrzymamy nigdy jedynki, a co za tym idzie, liczba 4 jest liczbą smutną. Ale nie ma powodu do obaw - zapewne każdy z nas potrafi znaleźć w tej liczbie pozytywne aspekty.

Zauważmy istotne wnioski wysuwające się z badania wesołości danej liczby. Jeżeli liczba 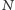jest wesoła, to każda liczba powstała podczas wykonywania algorytmu również jest wesoła. 19, 82, 69 oraz 100 są więc liczbami wesołymi i nie musimy dla nich wykonywać osobnych obliczeń. Podobnie będzie z liczbą 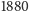(Czytelnik zechce sprawdzić, iż jest ona istotnie liczbą wesołą) oraz wszystkimi, jakie otrzymamy przy wykonywaniu algorytmu - wszystkie one będą wesołe. Gdy natomiast weźmiemy liczbę smutną, na przykład 4, to również liczby 16, 37, 58, 89, 145, 42 oraz 20 będą smutne. Dzięki tym uwagom będziemy w stanie znacznie szybciej wyznaczyć wszystkie liczby wesołe mniejsze lub równe 1000. Kompletne zestawienie 143 takich liczb reprezentuje poniższa tabela.

Przyglądając się jej, dostrzegamy kilka regularności. Zauważmy, że obok 19 w tabeli znajdziemy takie liczby, jak 109 oraz 190. Podobnie mamy 82, 802 oraz 820. W każdym przypadku dopisaliśmy jedno zero w wybranym przez nas miejscu i tak możemy zrobić dla dowolnej wybranej z tabeli liczby. Dopisanie zer do liczby wesołej nie zmienia sumy kwadratów jej cyfr, więc do liczby 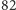możemy dopisać dowolną ilość zer, na przykład dostając liczbę 80002000000 i jest to inna liczba wesoła. Zwróćmy też uwagę na to, że w tabeli obok 82 jest również 28. Podobnie odnajdziemy liczby 133, 313 oraz 331 - one wszystkie są wesołe i różni je tylko kolejność cyfr. Zmiana kolejności cyfr (permutacja cyfr) również nie zmienia sumy kwadratów cyfr. Możemy to również połączyć z dopisywaniem zer i tak startując od liczby 133, dojść do liczby 3001030. Naturalne może wydawać się to, że zestawienie dwóch liczb wesołych daje liczbę wesołą. Tak jednak nie jest - liczba 7 jest wesoła, natomiast liczba 77 jest smutna.

W związku z regularnością występowania liczb wesołych, to jest tworzenia jednej liczby wesołej z już istniejącej przez dopisanie zera lub przepermutowanie cyfr, można z powyższego zestawienia wyróżnić tylko te liczby wesołe, które nie mają w swym zapisie zera i są najmniejsze spośród liczb otrzymanych przez permutację ich cyfr, wśród liczb mniejszych od tysiąca.

Wśród liczb wesołych wyróżniamy inne znane nam rodzaje liczb naturalnych. Do najczęściej wymienianych należą wesołe liczby pierwsze - liczby, które są jednocześnie wesołe i pierwsze:

Możemy pójść w inną stronę i wśród wesołych liczb poszukać liczb Fibonacciego. To zadanie wymaga większego nakładu pracy, najmniejszą wesołą liczbą Fibonacciego jest liczb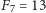a ; dla 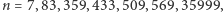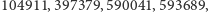liczby 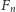są wesołe. Sądzi się, że poza 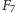nie ma innej wesołej liczby pierwszej, która jest również liczbą Fibonacciego.

Możemy również zapytać o największą liczbę wesołą, którą można zapisać przy wykorzystaniu każdej cyfry co najwyżej jeden raz. Rozwiązania tego problemu niech poszuka Czytelnik - jest to proste i pouczające ćwiczenie.

Poznane przez nas wcześniej metody otrzymywania nowych liczb wesołych pozwalają wyciągnąć jeden istotny wniosek - liczb wesołych jest nieskończenie wiele. Nie jest zatem możliwe wypisanie skończenie wielu liczb i stwierdzenie: "Wypisałem już wszystkie liczby wesołe, więcej nie ma!", gdyż zawsze znajdziemy większą liczbę wesołą. Aby zobaczyć to dokładniej, przyjrzyjmy się ciągowi liczb postaci 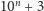dla 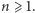Mamy więc kolejno 13, 103, 1003, 10003 i tak dalej. Wiemy już, że dopisywanie zer nie zmienia wartości sumy kwadratów cyfr, więc wszystkie te liczby dadzą po pierwszym kroku 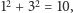a następnie 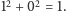Otrzymujemy więc prosty wniosek - wszystkie takie liczby są wesołe. Zwróćmy uwagę na to, co zrobiliśmy - pokazaliśmy właśnie, że liczb wesołych jest nieskończenie wiele. Dlaczego? Otóż w miejsce w liczbie 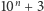możemy podstawić dowolną liczbę naturalną większą od zera, a ponieważ liczb naturalnych jest nieskończenie wiele, stąd też liczb wesołych musi być nieskończenie wiele. W związku z tym nasuwa się pytanie o to, jak często wśród liczb naturalnych pojawiają się liczby wesołe. Sprawdzono przy użyciu komputerów, że wśród liczb naturalnych nie większych niż 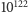jest około 15,5% liczb wesołych. Przypomnijmy - liczb wesołych nie większych od 1000 było 143, natomiast nie większych od 500 jest 76, co w istocie jest bardzo bliskie 15,5% wartości liczby 500.

Liczby wesołe pozostawiają między sobą bardzo wiele liczb smutnych. Jak widzieliśmy na przykładzie liczby 4, od pewnego momentu ciąg cyfr zaczął się powtarzać. Zauważmy, że startując od liczby 2, w drugim kroku otrzymamy 4 i po pewnym czasie do 4 wrócimy. Oznacza to w szczególności, że jeżeli liczby zaczną się powtarzać, to wśród tych liczb, które się powtarzają, nie musi występować oryginalna liczba. Ale skąd właściwie wiemy, że wszystkie liczby, które nie są wesołe, zaczną tworzyć ciągi liczbowe okresowe, a więc będą liczbami smutnymi? Mianowicie o tym mówi ważne twierdzenie dotyczące liczb naturalnych:

Ten fakt jest tylko pozornie trudny do uzasadnienia. Naszkicujemy teraz jego dowód. Weźmy na początku liczbę złożoną z cyfr. Gdy zsumujemy kwadraty jej cyfr, otrzymamy liczbę nie większą od 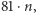gdyż każda z cyfr jest nie większa niż 9. 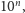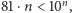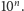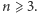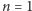Z drugiej strony liczba złożona z cyfr jest mniejsza od więc jeżeli tylko to w wyniku wykonywania algorytmu nigdy nie przekroczymy Tak jest istotnie dla wszystkich Dla oraz 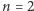możemy się łatwo przekonać, że nie dostaniemy nigdy liczby większej od 162 (jaka dwucyfrowa liczba realizuje to szacowanie?). Dla 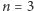może się zdarzyć, że suma kwadratów jest liczbą złożoną z takiej samej ilości cyfr jak liczba wyjściowa. Dla 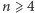zawsze dostaniemy liczbę mającą mniej cyfr niż liczba wyjściowa. W pierwszej z wymienionych sytuacji 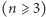wiemy, że dostaniemy zawsze nie więcej niż 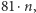więc po wykonaniu 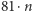razy algorytmu otrzymamy 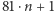liczb. Wśród nich jest albo jedynka, albo zgodnie z zasadą szufladkową Dirichleta muszą się pojawić dwie takie same liczby, co oznacza, że tworzy się okresowy ciąg liczb. W pozostałych przypadkach możemy albo sprawdzić wszystko ręcznie, albo posłużyć się podobnym rozumowaniem z pierwszego przypadku. Wykazaliśmy tym samym podstawowe twierdzenie dotyczące liczb wesołych.

Gdy pierwszy raz stykamy się z liczbami wesołymi, możemy zapytać, dlaczego właściwie podnosimy cyfry do kwadratu? Dlaczego nie podnosimy ich do trzeciej potęgi, czwartej, piątej lub innej potęgi naturalnej? To ograniczenie przyszło wraz z definicją liczby wesołej - pomysłodawca wybrał drugą potęgę. Wyobraźnia matematyka jednak tutaj się nie kończy, wszak możemy sprawdzać, czy liczby są wesołe w innym sensie - czy sumowanie sześcianów cyfr wchodzących w skład liczby da nam jedynkę. Taką liczbę nazwiemy 3-wesołą, gdzie trójka oznacza potęgę, do jakiej podnosimy cyfry danej liczby. Jeżeli zamiast 3 wybierzemy dowolną potęgę 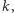to otrzymamy liczby 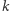-wesołe. Jeżeli liczba nie jest 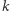-wesoła, to jest 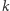-smutna.

Weźmy ponownie liczbę 13. Mamy 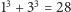i kolejno:

Dalsze obliczenia sprowadzą nas do znanej nam z poprzednich rozważań okresowości liczb, co przekłada się na to, że liczba 13 jest 3-smutna. A co ze szczęśliwą siódemką? Otrzymamy kolejno: 343, 118, 514, 190, 730, 370. Zadziwiające, liczba 370 będzie się cały czas powtarzać (jaka inna liczba ma tę własność, że suma sześcianów jej cyfr jest równa tej liczbie?). Ale nie zakończyliśmy na jedynce, więc liczba 7 jest 3-smutna. Zauważmy natomiast, że liczby postaci 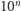są liczbami 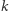-wesołymi dla wszystkich 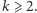I podobnie - do liczby 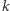-wesołej możemy dopisać dowolną ilość zer bez zmiany własności tej liczby oraz możemy permutować jej cyfry, zachowując 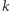-wesołość. Czytelnik zechce poszukać liczb 3-wesołych oraz 4-wesołych innej postaci niż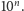

O liczbach wesołych możemy również mówić w systemach pozycyjnych innych niż dziesiętny. Liczba 7staje się liczbą wesołą w siódemkowym systemie pozycyjnym - ma w nim reprezentację równą 10, a więc już po pierwszym kroku dostajemy jedynkę. W systemie binarnym (dwójkowym) bardzo szybko odnajdujemy najmniejszą liczbę wesołą różną od jedynki - jest nią 10 (w reprezentacji dziesiętnej odpowiada ona liczbie 2). Prowadząc dalsze obliczenia, stwierdzamy, że również 11, 100, 101, 110 oraz 111 (w reprezentacji dziesiętnej są to kolejno: 3, 4, 5, 6 oraz 7) są liczbami wesołymi. Okazuje się, że zachodzi znacznie ogólniejszy i bardzo zaskakujący fakt: w systemie binarnym wszystkie liczby są wesołe. Podobnie jest w systemie czwórkowym i... na tym trop urywa się, gdyż wśród podstaw mniejszych od 500 000 000 nie znaleziono innej mającej taką własność.

Wracając do klasycznej definicji, możemy zadać jeszcze wiele pytań dotyczących liczb wesołych oraz liczb smutnych. Jeżeli liczba jest smutna, to ile co najwyżej różnych liczb będzie się powtarzać przy wykonywaniu algorytmu? Odpowiedzi dostarcza nam przykład z liczbą 4 - okazuje się bowiem, że dla dowolnej liczby początkowej 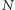proces sumowania kwadratów liczb albo zakończy się na liczbie 1, albo wejdzie w jedno z miejsc cyklu liczb 4, 16, 37, 58, 89, 145, 42, 20. Liczba 229 wkroczy w cykl począwszy od liczby 89, 24 od 20, a 11 od 4 i w każdym z tych przypadków doświadczymy powtarzającego się cyklu złożonego z ośmiu różnych liczb, wymienionych wyżej. Innym problemem jest istnienie dowolnie długich ciągów kolejnych liczb naturalnych wesołych. Odpowiedź pozytywną na to pytanie przedstawił w roku 2000 Esam El-Sedy wraz z Samirem Siksekiem. Ich dowód polegał, między innymi, na pokazaniu, iż liczba

jest liczbą wesołą dla dowolnego 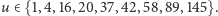Wspomnimy jeszcze o największej znanej wesołej liczbie pierwszej: 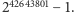Jest to trzecia największa znana liczba pierwsza, odkryta w roku 2009, której rozwinięcie dziesiętne składa się z 12837064 cyfr. Jako (niekoniecznie trudne) ćwiczenie niech Czytelnik sprawdzi, ile co najwyżej sumowań kwadratów cyfr dla tej liczby należy wykonać, aby otrzymać 1.

Wesołe liczby pierwsze pojawiły się w popularnym serialu "Doctor Who". W odcinku pt. "42" Doktor (grany przez Davida Tennanta) podaje definicją wesołej liczby pierwszej. W tym odcinku liczby wesołe pojawiły się jako zabezpieczenie do jednych z drzwi blokujących dostęp do maszynowni silnika statku kosmicznego. Aby otworzyć drzwi, bohaterowie musieli odpowiedzieć na następujące pytanie:

Tytułowy Doktor podał natychmiast odpowiedź "379", wyjaśniając następnie definicję wesołej liczby pierwszej. Jego opis zwieńczyło zdanie: "Czy nie uczą już matematyki rekreacyjnej?".