Drobiazgi
Choć proste to nieproste
Starożytni Egipcjanie sprzed 4000 lat uznawali tylko ułamki proste, czyli takie, które w liczniku miały jedynkę. Oczywiście, były też inne ułamki, ale o nich uczeni mówić nie chcieli – przedstawiali je jako sumę ułamków prostych. Nie byłoby w tym niczego nadzwyczajnego, gdyby nie pretensjonalne wymaganie, aby w owej sumie każdy ułamek był inny.
Czy każdy ułamek da się przedstawić jako suma różnych ułamków prostych? Tak, jest nawet bardzo prosty algorytm, pozwalający to zrobić: od ułamka należy odejmować największy jak się da ułamek prosty.
Zobaczmy to na przykładzie rozkładu
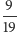 :
:

Zatem
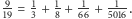
Patrząc na te rachunki, widzimy, że przy naszym algorytmie w każdym kroku
licznik maleje o 1 (Czytelniku, udowodnij to!). Stąd widać, że algorytm
ma własność stopu – jeśli w liczniku było
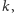 to taki rozkład
(a mogą być inne?) będzie zawierał co najwyżej
to taki rozkład
(a mogą być inne?) będzie zawierał co najwyżej
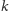 ułamków
prostych.
ułamków
prostych.
Dla
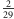 algorytm daje rozkład
algorytm daje rozkład
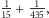 ale dobrym rozkładem jest
też
ale dobrym rozkładem jest
też
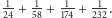
Widzimy jednak, że w pewnym momencie coś się skróciło i ułamków było mniej – nie 9, a tylko 4. I to się zdarza bardzo często już nawet dla małych liczników, np.

czyli
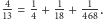
Badacze ułamków prostych, obserwując ich zachowanie, postawili ważne, do dziś nierozstrzygnięte pytanie:
Problem (Erdős–Straus). Czy każdy ułamek
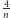 jest sumą trzech
różnych ułamków prostych?
jest sumą trzech
różnych ułamków prostych?
Andrzej Schinzel zaryzykował natomiast niepotwierdzoną dotychczas hipotezę:
Hipoteza. Dla dowolnego
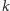 istnieje
takie
istnieje
takie
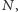 że dla dowolnego
że dla dowolnego
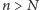 ułamek
ułamek
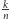 jest sumą
trzech różnych ułamków prostych.
jest sumą
trzech różnych ułamków prostych.
Czytelniku – do roboty!