Jaki jest następny wyraz tego ciągu?
3, 7, 31, 211, 2311, ... – jaki jest następny wyraz tego ciągu? Jakiś czas temu taka zagadka pojawiła się na jednej z polskich rozrywkowych stron internetowych. Niemal od razu w komentarzach pod nią rozpoczął się spór o poprawne, prawdziwe rozwiązanie. Czytelnik zapewne zechce podjąć wyzwanie samodzielnego odnalezienia następnego elementu ciągu i jego ogólnej reguły. Zatem zatrzymajmy się tu i pozwólmy sobie na chwilę namysłu; w dalszej części tekstu pojawi się rozwiązanie (autorowi niniejszego tekstu zajęło kilka dłuższych chwil znalezienie formuły).

Autor myślał tak: wszystkie te liczby są nieparzyste, a nawet pierwsze;
początkowe dwie są jednocyfrowe, następne mają jedynkę jako cyfrę jedności.
Z braku lepszych pomysłów odejmijmy
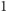 od każdej z tych
liczb – otrzymamy wtedy:
od każdej z tych
liczb – otrzymamy wtedy:
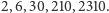 Łatwo można
zauważyć, że
Łatwo można
zauważyć, że
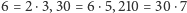 i szybko sprawdzić,
że
i szybko sprawdzić,
że
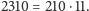 Czyli zaczynamy od
Czyli zaczynamy od
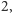 mnożymy
przez
mnożymy
przez
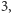 potem wynik mnożymy przez
potem wynik mnożymy przez
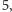 kolejny
wynik mnożymy przez
kolejny
wynik mnożymy przez
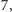 a ten z kolej przez
a ten z kolej przez
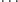 nie,
nie przez
nie,
nie przez
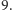 Przez
Przez
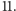 Czemu nie przez
Czemu nie przez
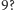 Widać
nie chodzi o kolejne liczby nieparzyste. Więc może kolejne liczby
pierwsze? Jak dotąd, iloczyny budowaliśmy z kolejnych liczb pierwszych:
Widać
nie chodzi o kolejne liczby nieparzyste. Więc może kolejne liczby
pierwsze? Jak dotąd, iloczyny budowaliśmy z kolejnych liczb pierwszych:
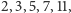 więc pewnie to o to tu chodzi. Kolejną liczbą pierwszą
jest
więc pewnie to o to tu chodzi. Kolejną liczbą pierwszą
jest
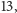 zatem Czytelnik Sprawny szybko obliczy w pamięci
(a mniej sprawny za pomocą kalkulatora, jak to i autor uczynił), że
zatem Czytelnik Sprawny szybko obliczy w pamięci
(a mniej sprawny za pomocą kalkulatora, jak to i autor uczynił), że
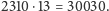 Teraz trzeba jeszcze tylko dodać do tego jedynkę
i mamy rozwiązanie zagadki: następną liczbą jest
Teraz trzeba jeszcze tylko dodać do tego jedynkę
i mamy rozwiązanie zagadki: następną liczbą jest
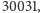 zaś
zaś
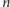 -ty
wyraz ciągu powstaje przez dodanie jedynki do iloczynu
-ty
wyraz ciągu powstaje przez dodanie jedynki do iloczynu
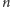 kolejnych
liczb pierwszych.
kolejnych
liczb pierwszych.
Po uzyskaniu powyższego wyniku zadowolony z siebie autor (niechaj
Czytelnik Przezorny zawsze strzeże się nadmiernego zadowolenia z siebie –
niewiele jest rzeczy równie pewnie wiodących do zguby!) postanowił
skonfrontować swoje rozumowanie z tymi przedstawionymi w komentarzach.
Był więcej niż zdziwiony, gdy zobaczył odpowiedź:
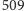 – i to
bez słowa wyjaśnienia. Cóż więc pozostało uczynić, jak nie zwrócić się
po pomoc do mądrzejszych od siebie? Wolfram Alpha rzeczywiście
podaje
– i to
bez słowa wyjaśnienia. Cóż więc pozostało uczynić, jak nie zwrócić się
po pomoc do mądrzejszych od siebie? Wolfram Alpha rzeczywiście
podaje
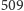 jako kolejny prawdopodobny wyraz podanego ciągu,
z wyjaśnieniem odsyłając do The On-Line Encyclopedia of Integer Sequences.
Tam możemy przeczytać, że
jako kolejny prawdopodobny wyraz podanego ciągu,
z wyjaśnieniem odsyłając do The On-Line Encyclopedia of Integer Sequences.
Tam możemy przeczytać, że
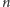 -ty element badanego ciągu to
największy dzielnik pierwszy iloczynu
-ty element badanego ciągu to
największy dzielnik pierwszy iloczynu
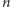 kolejnych liczb pierwszych
powiększonego o jeden, a dalej, że pomysł tego ciągu wywodzi się z dowodu
Euklidesa, iż istnieje nieskończenie wiele liczb pierwszych. Zamiast się
wyjaśnić, sprawa stała się jeszcze bardziej zagmatwana. Co do rzeczy
ma Euklides? Przypomnijmy może twierdzenie i dowód (mówiąc
ściślej, współczesną interpretację tego dowodu), które zamieścił
w swoich Elementach.
kolejnych liczb pierwszych
powiększonego o jeden, a dalej, że pomysł tego ciągu wywodzi się z dowodu
Euklidesa, iż istnieje nieskończenie wiele liczb pierwszych. Zamiast się
wyjaśnić, sprawa stała się jeszcze bardziej zagmatwana. Co do rzeczy
ma Euklides? Przypomnijmy może twierdzenie i dowód (mówiąc
ściślej, współczesną interpretację tego dowodu), które zamieścił
w swoich Elementach.
Dowód Euklidesa. Swój dowód Euklides przeprowadził metodą
reductio ad absurdum. Podążając tropem jego myśli, załóżmy, że
istnieje skończenie wiele liczb pierwszych. Oznaczmy je w kolejności
rosnącej jako:
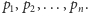 Zdefiniujmy
liczbę
Zdefiniujmy
liczbę
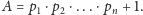 Nie dzieli się ona przez żadną z liczb
pierwszych
Nie dzieli się ona przez żadną z liczb
pierwszych
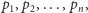 bo reszta z dzielenia zawsze wynosi
bo reszta z dzielenia zawsze wynosi
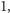 nie jest
więc złożona. Jest też większa od każdej z liczb
nie jest
więc złożona. Jest też większa od każdej z liczb
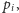 nie jest
więc także pierwsza. Ale przecież każda liczba naturalna (większa
od
nie jest
więc także pierwsza. Ale przecież każda liczba naturalna (większa
od
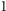 ) jest albo pierwsza, albo złożona, z definicji pierwszości.
Otrzymana sprzeczność pokazuje, że poczynione przez nas założenie
było fałszywe, a więc, że jest nieskończenie wiele liczb pierwszych.
) jest albo pierwsza, albo złożona, z definicji pierwszości.
Otrzymana sprzeczność pokazuje, że poczynione przez nas założenie
było fałszywe, a więc, że jest nieskończenie wiele liczb pierwszych.
Czytając powyższy dowód nie dość uważnie, można by w pierwszej
chwili pomyśleć, że skonstruowana w powyższym dowodzie
liczba
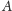 jest kolejną liczbą pierwszą, którą można równie
dobrze oznaczyć jako
jest kolejną liczbą pierwszą, którą można równie
dobrze oznaczyć jako
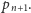 Otóż
Otóż
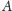 nie musi być
kolejną liczbą pierwszą, mogą istnieć inne liczby pierwsze większe niż
każda z
nie musi być
kolejną liczbą pierwszą, mogą istnieć inne liczby pierwsze większe niż
każda z
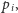 ale mniejsze niż
ale mniejsze niż
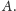 W istocie
W istocie
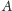 nie musi
być w ogóle liczbą pierwszą – może być iloczynem kilku liczb pierwszych
większych niż liczby
nie musi
być w ogóle liczbą pierwszą – może być iloczynem kilku liczb pierwszych
większych niż liczby
 Obrazują to dwa przykłady.
Obrazują to dwa przykłady.
Przykład 1.
Załóżmy, że jest tylko pięć liczb pierwszych:
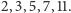 Wtedy
konstruujemy liczbę
Wtedy
konstruujemy liczbę
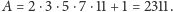 Liczba ta nie dzieli
się przez żadną z wybranych liczb pierwszych. W istocie nie dzieli się przez
żadną liczbę mniejszą od siebie (nie licząc jedynki), zatem jest to liczba
pierwsza, jednak inna niż te z poczynionego założenia – sprzeczność.
Przy czym istnieją też inne, mniejsze liczby pierwsze, np.
Liczba ta nie dzieli
się przez żadną z wybranych liczb pierwszych. W istocie nie dzieli się przez
żadną liczbę mniejszą od siebie (nie licząc jedynki), zatem jest to liczba
pierwsza, jednak inna niż te z poczynionego założenia – sprzeczność.
Przy czym istnieją też inne, mniejsze liczby pierwsze, np.
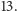
Przykład 2. Załóżmy, że jest tylko
sześć liczb pierwszych:
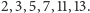 Wtedy konstruujemy liczbę
Wtedy konstruujemy liczbę
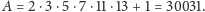 Liczba ta nie dzieli się przez żadną
z wybranych
liczb pierwszych. Ale okazuje się, że
Liczba ta nie dzieli się przez żadną
z wybranych
liczb pierwszych. Ale okazuje się, że
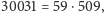 przy czym
tak
przy czym
tak
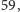 jak i
jak i
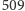 są pierwsze, choć nie zostały wymienione
w założeniu. Znów sprzeczność.
są pierwsze, choć nie zostały wymienione
w założeniu. Znów sprzeczność.
A więc to o to w tym wszystkim chodziło – o ilustrację powyższego dowodu,
w szczególności niuansu zilustrowanego przykładami. Teraz już wiadomo,
jak i dlaczego badany ciąg został określony. No dobrze, czy w takim razie 30031
jest złą odpowiedzią? Nie, odpowiedź ta jest zgodna z treścią zadania – jest to
ciąg o zadanych początkowych elementach i prostej regule tworzenia kolejnych
wyrazów. Tyle, że to inny ciąg niż oczekiwany przez twórcę zadania.
Zbieżność początkowych wyrazów obu ciągów wynika z faktu, że owe
wyrazy są liczbami pierwszymi, a więc ich największymi dzielnikami pierwszymi
są one same. Dopiero następny iloczyn,
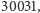 czy też jego największy
dzielnik pierwszy,
czy też jego największy
dzielnik pierwszy,
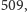 ujawniają różnice. Gdyby w zagadce
podano o jedną liczbę więcej, byłoby jasne, o który ciąg chodzi: ciąg
ujawniają różnice. Gdyby w zagadce
podano o jedną liczbę więcej, byłoby jasne, o który ciąg chodzi: ciąg
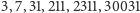 będzie kontynuowany przez
będzie kontynuowany przez
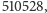 zaś
ciąg
zaś
ciąg
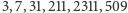 przez
przez
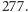
Właśnie ta niejednoznaczność wywołała burzliwą dyskusję, zresztą zupełnie
niepotrzebną. Dla matematyka jest oczywiste, że gdy w zadaniu należy
znaleźć obiekt o pewnych własnościach określonych w treści zadania, to
próbuje znaleźć wszystkie obiekty spełniające zadane warunki. Na przykład,
kiedy szuka rozwiązań równania
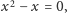 nie zadowala się
samą jedynką, czy też samym zerem – jako rozwiązania podaje obie
te liczby. Problem leży raczej po stronie samych zagadek pt. jaka jest
następna liczba?. Jeżeli podamy kilka liczb, możemy dobrać do nich
nieprzeliczalnie wiele nieskończonych ciągów, których początkowe wyrazy
będą takie, jak te podane, np.
nie zadowala się
samą jedynką, czy też samym zerem – jako rozwiązania podaje obie
te liczby. Problem leży raczej po stronie samych zagadek pt. jaka jest
następna liczba?. Jeżeli podamy kilka liczb, możemy dobrać do nich
nieprzeliczalnie wiele nieskończonych ciągów, których początkowe wyrazy
będą takie, jak te podane, np.
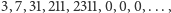 albo
albo
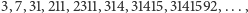 żeby już trzymać się
naszego ciągu.
żeby już trzymać się
naszego ciągu.
Oczywiście, nie o to chodzi w zagadkach, ale o to, by na podstawie podanych
początkowych wyrazów znaleźć metodę otrzymywania kolejnych, by znaleźć
ogólny schemat. Ale nawet przy takim ograniczeniu nadal mamy nieskończenie
wiele różnych wzorów. Do węzłów
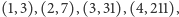
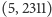 możemy (nawet nie musimy) dołożyć sobie dowolne kolejne,
np.
możemy (nawet nie musimy) dołożyć sobie dowolne kolejne,
np.
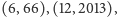 znaleźć jakąś funkcję określoną na całej
prostej i przechodzącą przez podane punkty (najprościej numerycznie,
za pomocą komputera), by na koniec ograniczyć dziedzinę do argumentów
naturalnych, otrzymując w ten sposób ciąg spełniający warunki zadania, wraz ze
sposobem obliczania kolejnych jego wyrazów. Możemy nawet z góry zadać
następny element, jak w przypadku węzła
znaleźć jakąś funkcję określoną na całej
prostej i przechodzącą przez podane punkty (najprościej numerycznie,
za pomocą komputera), by na koniec ograniczyć dziedzinę do argumentów
naturalnych, otrzymując w ten sposób ciąg spełniający warunki zadania, wraz ze
sposobem obliczania kolejnych jego wyrazów. Możemy nawet z góry zadać
następny element, jak w przypadku węzła
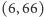 – to właśnie on
wygeneruje kolejny wyraz równy
– to właśnie on
wygeneruje kolejny wyraz równy
I tu właśnie leży sedno: ściśle poprawna odpowiedź musiałaby zawierać wszystkie ciągi rozpoczynające się zadanymi liczbami, a zagadka, jako łamigłówka, powinna mieć jedną, stosunkowo łatwą do znalezienia odpowiedź. Rzecz jasna, jej znalezienie wcale nie musi być łatwe, ale rozwiązania nie powinny wymagać zaawansowanych studiów (w każdym razie tak autor postrzega zagadki i chyba nie jest w tym odosobniony). Stąd niejawne założenie jednoznaczności. Czy nonsensowne? Raczej nie, choć wymaga ostrożności przy takim konstruowaniu zagadek, by oczekiwane rozwiązanie było naturalne i wyraźnie łatwiejsze do znalezienia niż pozostałe, nienaturalne i nieoczekiwane. Ta naturalność wymaga pewnej intuicji i wyczucia przy tworzeniu zagadek. Czy w takim razie opisana zagadka jest zła? Chyba nie, skoro skłoniła do przemyśleń co najmniej jedną osobę (autora), czego efektem jest niniejszy tekst.