Mała Delta
Kraina dwóch monet
Wyobraźmy sobie, że trafiliśmy do dziwnego kraju, w którym jedynymi dostępnymi środkami płatniczymi są monety o nominałach 5 i 9. Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty...
Widzimy świeżą, pyszną napoleonkę w cenie 7 złociaków (tutejsza waluta), jednak mimo ogromnego na nią apetytu i paru monet w kieszeni, nie jesteśmy w stanie zapłacić odpowiedniej kwoty. Sprzedawca podpowiada, byśmy w tej niezręcznej sytuacji skusili się na dwie napoleonki – razem kosztować będą 14 złociaków, które możemy uiścić przy użyciu jednej monety 5-złociakowej i jednej 9-złociakowej. Zgadzamy się na to salomonowe rozwiązanie i ze słodkościami w ręce zaczynamy zastanawiać się, jakie właściwie są ceny produktów, które możemy zakupić? Oczywiście (i niestety…), zależy to przede wszystkim od posiadanej przez nas kwoty; na potrzeby naszych rozważań założymy jednak, że wygraliśmy na loterii, wszystkie kieszenie mamy wypchane pieniędzmi i zupełnie nie musimy się martwić tym, że ich zabraknie.

Rys. 1

Rys. 2
Najtańszy produkt, który możemy zakupić, ma wartość 5 złociaków;
kolejne dostępne nam ceny zostały zaznaczone na rysunku 1 Po pewnym czasie
spędzonym nad kartką papieru zaczynamy podejrzewać, że jesteśmy w stanie
zapłacić każdą kwotę nie mniejszą niż 32 złociaki. Zachęceni naszymi
sukcesami obliczeniowymi zaczęliśmy rozważać, jak wyglądałaby sytuacja,
gdyby nasze dwie monety miały inne nominały? Jeśli w obiegu mielibyśmy
3- i 12-złociakówki, każda możliwa do zapłacenia cena musiałaby być
podzielna przez 3; nie istniałaby zatem kwota, począwszy od której jesteśmy
w stanie zapłacić każdą sumę pieniędzy (nazwijmy tę kwotę przewodnikiem).
Jeśli jednak monetę 12-złociakową zamienimy na 14-złociakową, pracowite
rachunki pokażą, że możemy zapłacić każdą kwotę nie mniejszą niż 26
(Rys. 2). W tym momencie uruchamia się nasza niezawodna, matematyczna
intuicja, która podpowiada, że jeśli dostępne nominały są względnie pierwsze
i wynoszą
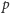 i
i
 złociaków, to ich przewodnik wynosi
złociaków, to ich przewodnik wynosi
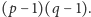 W języku matematyki naszą obserwację prezentuje
następujące:
W języku matematyki naszą obserwację prezentuje
następujące:
Twierdzenie (Frobenius).
Dane są dwie liczby względnie pierwsze
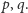 Wtedy dla każdej
liczby naturalnej
Wtedy dla każdej
liczby naturalnej
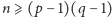 istnieją takie liczby naturalne
istnieją takie liczby naturalne
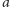 i
i
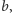 że
że

Zanim przedstawimy dowód, wybierzmy się do kiosku, w którym kasa nie
jest zupełnie pusta i sprzedawca bez problemu może wydawać resztę.
Zwróćmy uwagę, że możemy w nim zakupić nasz ulubiony miesięcznik
Delta, który kosztuje 1 złociaka – wystarczy, że wręczymy kioskarzowi dwie
monety 5-złociakowe, a on odda nam jedną monetę 9-złociakową reszty.
Wnioskujemy stąd, że możemy w tym kiosku zakupić przedmiot
w dowolnej cenie
 złociaków – wystarczy wyciągnąć z kieszeni
złociaków – wystarczy wyciągnąć z kieszeni
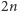 monet 5-złociakowych i zażądać
monet 5-złociakowych i zażądać
 monet 9-złociakowych
reszty. Czy ta komfortowa dla nas sytuacja ma miejsce dla dowolnej pary
względnie pierwszych nominałów? Twierdzącej odpowiedzi dostarcza
poniższy
monet 9-złociakowych
reszty. Czy ta komfortowa dla nas sytuacja ma miejsce dla dowolnej pary
względnie pierwszych nominałów? Twierdzącej odpowiedzi dostarcza
poniższy
Lemat. Dane są dwie liczby względnie pierwsze
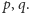 Wtedy dla każdej liczby naturalnej
Wtedy dla każdej liczby naturalnej
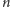 istnieją takie liczby
naturalne
istnieją takie liczby
naturalne
 i
i
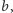 że
że
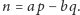
Pokazuje on, że jeśli mamy do dyspozycji mnóstwo monet
 –złociakowych, a sprzedawca ma pod ręką ogromny stos monet
–złociakowych, a sprzedawca ma pod ręką ogromny stos monet
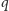 –złociakowych do wydawania reszty, to jesteśmy w stanie kupić
dowolny artykuł w jego sklepie. Aby przekonać się o słuszności lematu,
rozważmy liczby
–złociakowych do wydawania reszty, to jesteśmy w stanie kupić
dowolny artykuł w jego sklepie. Aby przekonać się o słuszności lematu,
rozważmy liczby
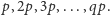
Zauważmy, że pozostawiają one różne reszty z dzielenia przez
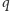 – istotnie,
gdyby pewne dwie z nich, powiedzmy
– istotnie,
gdyby pewne dwie z nich, powiedzmy
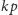 i
i
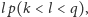 pozostawiały
tę samą resztę, to ich różnica
pozostawiały
tę samą resztę, to ich różnica
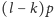 byłaby podzielna przez
byłaby podzielna przez
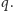 Ponieważ
Ponieważ
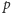 i
i
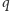 są względnie pierwsze, liczba
są względnie pierwsze, liczba
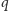 musiałaby dzielić
musiałaby dzielić
 ; jest to jednak niemożliwe, gdyż
; jest to jednak niemożliwe, gdyż
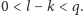 Skoro każda z
Skoro każda z
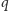 przedstawionych na początku liczb
pozostawia inną resztę z dzielenia przez
przedstawionych na początku liczb
pozostawia inną resztę z dzielenia przez
 to wyczerpują one wszystkie
możliwe reszty.
to wyczerpują one wszystkie
możliwe reszty.
Przykład. Przykład dla 5- i 9-złociakówki: liczby 5, 10, 15, 20, 25, 30, 35, 40, 45 dają różne reszty z dzielenia przez 9 (kolejno 5, 1, 6, 2, 7, 3, 8, 4, 0), a ponieważ jest ich 9, stanowią wszystkie możliwe reszty.
W szczególności dla pewnego
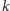 naturalnego liczba
naturalnego liczba
 pozostawia resztę 1 z dzielenia przez
pozostawia resztę 1 z dzielenia przez
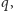 tzn. jest postaci
tzn. jest postaci
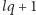 dla pewnego naturalnego
dla pewnego naturalnego
 Otrzymujemy zatem
Otrzymujemy zatem
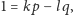 więc przy użyciu
więc przy użyciu
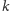 monet
monet
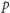 –złociakowych
możemy zakupić Deltę, otrzymując
–złociakowych
możemy zakupić Deltę, otrzymując
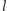 monet
monet
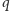 –złociakowych
reszty. Możemy zatem nabyć przedmiot o dowolnej cenie: z poprzedniej
równości wnioskujemy, że dla dowolnej liczby naturalnej
–złociakowych
reszty. Możemy zatem nabyć przedmiot o dowolnej cenie: z poprzedniej
równości wnioskujemy, że dla dowolnej liczby naturalnej
 mamy
mamy
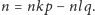 Ponieważ
Ponieważ
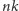 i
i
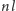 są liczbami naturalnymi,
teza lematu została udowodniona.
są liczbami naturalnymi,
teza lematu została udowodniona.
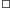
Wyposażeni w powyższy rezultat, możemy śmiało powrócić do
cukierni z pustą kasą, czyli do problemu Frobeniusa. Wybierzmy dowolne
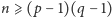 i korzystając z lematu, dobierzmy takie liczby
naturalne
i korzystając z lematu, dobierzmy takie liczby
naturalne
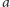 i
i
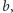 że
że
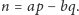 Proste rachunki
doprowadzą nas do wniosku, że dla dowolnej liczby naturalnej
Proste rachunki
doprowadzą nas do wniosku, że dla dowolnej liczby naturalnej

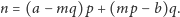 | (1) |
Znajdziemy takie
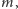 że oba współczynniki
że oba współczynniki
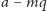 i
i
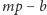 będą
nieujemne, czym zakończymy dowód twierdzenia. W tym celu rozważmy
najmniejszą wielokrotność
będą
nieujemne, czym zakończymy dowód twierdzenia. W tym celu rozważmy
najmniejszą wielokrotność
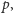 która jest nie mniejsza niż
która jest nie mniejsza niż
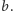 Innymi słowy, wybierzmy najmniejsze możliwe
Innymi słowy, wybierzmy najmniejsze możliwe
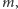 dla
którego czynnik
dla
którego czynnik
 jest nieujemny, tzn. takie
jest nieujemny, tzn. takie
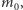 że
że
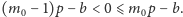 Z ostrej nierówności w łatwy sposób
wynika
Z ostrej nierówności w łatwy sposób
wynika
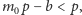 a zatem
a zatem
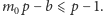 Przypuśćmy, że
Przypuśćmy, że
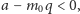 tzn.
tzn.
 Wstawiając
Wstawiając
 do (1)
i korzystając z otrzymanych nierówności, mielibyśmy
do (1)
i korzystając z otrzymanych nierówności, mielibyśmy

co przeczy założeniom twierdzenia. Otrzymana sprzeczność dowodzi
nierówności
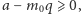 a skoro
a skoro
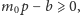 dowód został
zakończony.
dowód został
zakończony.
Przykład. Ponownie odwołując się do 5- i 9-złociakówek: chcemy kupić
tort za 34 złociaki.
Wiemy, że
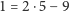 , więc
, więc
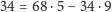 . Najmniejsza
wielokrotność 5, która jest niemniejsza od 34, to
. Najmniejsza
wielokrotność 5, która jest niemniejsza od 34, to
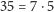 . Bierzemy
zatem
. Bierzemy
zatem
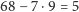 monet 5-złociakowych,
monet 5-złociakowych,
 monetę
9-złociakową i tort jest nasz!
monetę
9-złociakową i tort jest nasz!
Kiedy już mieliśmy wrażenie, że całkowicie panujemy nad naszymi wydatkami, przez kraj przetoczyła się reforma walutowa i dla ułatwienia transakcji wprowadzono trzecią monetę, 7–złociakową. Czy ułatwi to również nasze rozważania? Przewodnikiem dla trzech liczb względnie pierwszych będzie na pewno liczba nie większa od przewodników wyznaczonych dla każdej z par liczb. Przewodnik liczb 5 i 7 to 24, liczb 5 i 9 to 32, a liczb 7 i 9 to 48. Posiadając monety 5- i 7-złociakowe, jesteśmy w stanie uzyskać wszystkie liczby naturalne od 24, więc dodanie 9-złociaka do rozważań na pewno nie zwiększy nam tej liczby (nie spowoduje, że którejś wartości nie jesteśmy w stanie uzyskać), może ją co najwyżej zmniejszyć.

Deser dla troszkę starszych
Przyjrzyjmy się ponownie rysunkom 1 i 2. Zwróćmy uwagę, że w obu
przypadkach liczba kwot niemożliwych do zrealizowania stanowiła połowę
wartości przewodnika. Okazuje się, że jest to ogólna prawidłowość – dla
dowolnej pary liczb względnie pierwszych
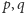 zbiór liczb, których nie
można przedstawić w postaci
zbiór liczb, których nie
można przedstawić w postaci
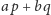 dla
dla
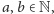 ma
ma
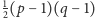 elementów. Aby się o tym przekonać, rozważmy
wielomian
elementów. Aby się o tym przekonać, rozważmy
wielomian

Niech
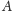 będzie zbiorem liczb naturalnych, nie większych od
będzie zbiorem liczb naturalnych, nie większych od
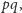 które można przedstawić w postaci
które można przedstawić w postaci
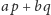 dla
dla
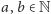 (zakładamy
(zakładamy
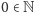 ). Chwila refleksji pozwala stwierdzić,
że wielomian
). Chwila refleksji pozwala stwierdzić,
że wielomian
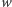 można przedstawić w postaci
można przedstawić w postaci

Oznacza to, że
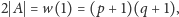 stąd
stąd
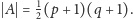 Z twierdzenia Frobeniusa wynika, że kwoty
niemożliwe do zrealizowania są mniejsze od
Z twierdzenia Frobeniusa wynika, że kwoty
niemożliwe do zrealizowania są mniejsze od
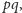 ich liczba wynosi
zatem
ich liczba wynosi
zatem