1.

Niech 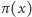oznacza liczbę liczb pierwszych nie większych od 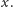 Tak więc dla oraz

co udowodnił już Euklides. Natomiast Czebyszew w połowie XIX wieku wykazał między innymi, że

Jeszcze wcześniej Legendre udowodnił, że

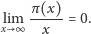(1)

I tu zaczyna się nasza historia. Z (1) wynika mianowicie, że dla każdego 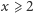istnieje 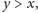 takie że

Czy dla dostatecznie dużych 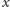można przyjąć 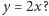 Głównym celem tej notki jest uzasadnienie odpowiedzi twierdzącej na to pytanie – okaże się, że wymaga to użycia dość subtelnych metod. Mamy więc udowodnić, że istnieje 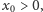 takie że dla 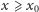zachodzi nierówność

lub, co na jedno wychodzi, nierówność jej równoważna

(2)

Nierówność (2) można wysłowić w ten sposób: dla 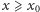w przedziale 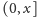jest więcej liczb pierwszych niż w przedziale 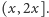 Pokażemy najpierw, że (2) nie wynika z następującej popularnej wersji twierdzenia o liczbach pierwszych

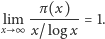(3)

Na mocy (3) możemy bowiem napisać

skąd otrzymujemy

Widać, że wyraz główny może być zdominowany przez człon resztowy 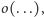 a więc nie można wnioskować, że lewa strona jest dodatnia dla dostatecznie dużych 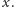 Z powyższego oszacowania wynika „tylko”, że

Aby wykazać (2), trzeba skorzystać z następującej mocniejszej wersji twierdzenia o liczbach pierwszych

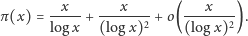(4)

Po prostych rachunkach otrzymujemy stąd

co daje

a z tego (2) wynika natychmiast. Obie powyższe wersje twierdzenia o liczbach pierwszych (oszacowania (3) oraz (4)) są wnioskami z twierdzenia o liczbach pierwszych Hadamarda–de la Vallée-Poussina, udowodnionego przez tych matematyków niezależnie w 1896 roku w postaci

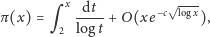(5)

gdzie 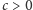jest stałą absolutną. Rzeczywiście, dwukrotne całkowanie przez części prowadzi do

co na mocy (5) i prostej obserwacji

prowadzi do (4). Na zakończenie części 1. zauważmy, że hipotetyczne ulepszenie (5)

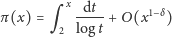(6)

nie zostało, póki co, udowodnione dla żadnego 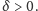 Natomiast to, że (6) zachodzi dla każdego 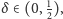 jest równoważne hipotezie Riemanna, co udowodnił von Koch w 1901 roku.

2.

To, że wielu interesujących pytań dotyczących liczb pierwszych nie można by w ogóle postawić, gdyby było ich tylko skończenie wiele, wykazano powyżej. Krótko mówiąc: analityczna teoria liczb nie miałaby racji bytu. W punkcie 2. pokażemy pokrótce, że algebraiczna teoria liczb byłaby też dużo mniej pasjonująca. Z ogólnej teorii pierścieni Dedekinda wynika bowiem, że jeśli w takim pierścieniu jest tylko skończenie wiele ideałów pierwszych, to obowiązuje w nim twierdzenie o jednoznaczności rozkładu. To wygodne twierdzenie zachodziłoby więc w szczególności w pierścieniach cyklotomicznych 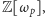 które są zbiorami liczb postaci

gdzie 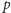jest ustaloną liczbą pierwszą, a 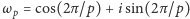 jest pierwiastkiem pierwotnym 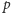-tego stopnia z 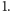  Już Kummer udowodnił w połowie XIX wieku wspaniałe, ogólne twierdzenie o równaniu Fermata

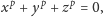(7)

z którego wynika, między innymi, że w przypadku jednoznaczności rozkładu w pierścieniu 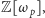 równanie (7) możliwe jest tylko dla 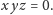 Tak więc historia Wielkiego Twierdzenia Fermata zakończyłaby się ponad 150 lat temu i to niezależnie od tego, jak wielka byłaby rzekomo skończona moc zbioru wszystkich liczb pierwszych! Ale na szczęście (?) jest inaczej: liczb pierwszych jest nieskończenie wiele, a największą liczbą pierwszą 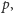 taką, że w 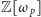 zachodzi twierdzenie o jednoznaczności rozkładu, jest Kummer, co prawda, we wspomnianym wyżej wspaniałym twierdzeniu zadowala się założeniem znacznie słabszym niż założenie o jednoznaczności rozkładu: aby udowodnić, że równanie (7) nie ma nietrywialnych rozwiązań, wystarczy mu założenie, iż tzw. 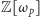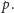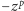liczba klas ideałów pierścienia nie jest podzielna przez  Warto wspomnieć, że metoda Kummera opiera się na następującym rozkładzie liczby na czynniki:

oraz że na tej drodze nie udało się uzyskać pełnego dowodu Wielkiego Twierdzenia Fermata! Dowód Andrew Wilesa z 1995 r. opiera się na wnikliwym badaniu konsekwencji istnienia nietrywialnego rozwiązania równania (7) w nowoczesnej teorii krzywych eliptycznych – w ten sposób uzyskuje się upragnioną sprzeczność.