Drobiazgi
Do nieskończoności jeszcze sporo brakuje

Zamieszczony w poprzednim numerze, jako zapowiedź tego numeru, widoczny
obok kwadrat magiczny jest dla
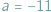 (lub
(lub
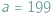 ) i
) i
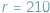 złożony z samych liczb pierwszych.
złożony z samych liczb pierwszych.
Można na to spojrzeć inaczej: istnieje ciąg arytmetyczny o długości co najmniej 9 złożony z liczb pierwszych (a nawet dwa takie ciągi).
Powstaje pytanie, czy istnieją dłuższe ciągi arytmetyczne złożone z samych liczb pierwszych.
Dawno, dawno temu – bo prawie przed ćwierćtysiącleciem – Lagrange i Waring doszli do wniosku, że powinny istnieć dowolnie długie takie ciągi złożone z liczb pierwszych. Do wniosku doszli, ale udowodnić tego nie umieli, podobnie jak wielu ich następców. (Zastanów się Czytelniku, dlaczego nie istnieje nieskończenie długi taki ciąg.)
Dowód udało się uzyskać dopiero 8 lat temu – dokonali tego Ben Green
i Terence Tao. Ale już poprzednio trwały zawody w znajdowaniu
jak najdłuższego takiego ciągu. W 1979 roku (z którego pochodzą
oba teksty
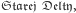 przytoczone w tym numerze) rekordowy
ciąg arytmetyczny liczb pierwszych miał 17 wyrazów (i liczył sobie
2 lata):
przytoczone w tym numerze) rekordowy
ciąg arytmetyczny liczb pierwszych miał 17 wyrazów (i liczył sobie
2 lata):

Autor artykułu Zagadki liczbowe publikowanego w tym numerze Delty, Jarosław Wróblewski, ustanowił w tej kategorii rekord świata w styczniu 2007 roku, budując ciąg

symbol
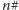 oznacza iloczyn liczb pierwszych nieprzekraczających
oznacza iloczyn liczb pierwszych nieprzekraczających
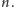 Rok później, w maju 2008 wraz z Raananem Chermonim poprawił
ten wynik o 1, budując ciąg
Rok później, w maju 2008 wraz z Raananem Chermonim poprawił
ten wynik o 1, budując ciąg

Pół roku później powstał międzynarodowy projekt PrimeGrid zbiorowego poszukiwania takich ciągów i (chyba) do niego należy obecnie rekord – uzyskany w kwietniu 2010 ciąg

Odrębną konkurencją jest poszukiwanie jak najdłuższego ciągu arytmetycznego złożonego z kolejnych liczb pierwszych (czyli takiego, że dla dowolnych dwóch jego kolejnych wyrazów nie ma liczby pierwszej leżącej między nimi) – tu aktualnie (chyba) rekordowa długość to 10. Poszczególne wyrazy oddziela zaledwie 210 (a może to ten, od którego zaczęliśmy?).
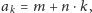 złożony z liczb pierwszych, nie istnieje, bo jego m-ty
wyraz dzieli się przez m.
złożony z liczb pierwszych, nie istnieje, bo jego m-ty
wyraz dzieli się przez m.