Mała Delta
Złożony problem liczb pierwszych
Co to jest liczba pierwsza? Najkrótsza definicja mówi, że to taka liczba naturalna, która ma dokładnie dwa dzielniki. Każda liczba naturalna ma przynajmniej dwa dzielniki: 1 i samą siebie. Wyjątkiem jest jedynka, dla której te dwa dzielniki okazują się tym samym.
Nie chcemy też rozpatrywać w tym kontekście zera (pomijając dyskusyjną
kwestię, czy należy ono do zbioru liczb naturalnych). Wobec tego można
powiedzieć, że liczby pierwsze to takie, które oprócz dwóch oczywistych
dzielników nie mają żadnych nieoczywistych – nie rozkładają się na
iloczyn liczb większych od 1 i mniejszych od nich samych. Pozostałe
liczby naturalne (oprócz jedynki, która tworzy swoją własną klasę)
nazywamy liczbami złożonymi, ponieważ można je rozłożyć na iloczyn
mniejszych czynników. Te czynniki nie muszą być różne – na przykład
najmniejsza liczba złożona to
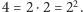 Natomiast ciekawą rzeczą
jest to, że zestaw liczb pierwszych, których iloczyn jest daną liczbą,
istnieje tylko jeden – takie rozkłady mogą się różnić tylko kolejnością
czynników.
Natomiast ciekawą rzeczą
jest to, że zestaw liczb pierwszych, których iloczyn jest daną liczbą,
istnieje tylko jeden – takie rozkłady mogą się różnić tylko kolejnością
czynników.
Liczby pierwsze są w pewnym sensie ciekawsze niż liczby złożone. Po pierwsze, występują rzadziej. Po drugie, bardzo trudno przewidzieć ich wystąpienia – może być tak, że dwie kolejne liczby pierwsze są oddzielone tylko przez jedną liczbę złożoną, a może być tak, że między nimi jest bardzo duża przerwa. Pary liczb pierwszych oddzielonych tylko jedną liczbą złożoną to liczby pierwsze bliźniacze. Nie wiadomo, jak dużo ich jest – znamy wiele przykładów, także wśród dużych liczb, ale nikt dotąd nie udowodnił, że jest ich nieskończenie wiele. Jak zwykle w takich przypadkach, trwają poszukiwania coraz większych takich par. Największa znana obecnie para liczb bliźniaczych, znaleziona w 2009 roku, to

A czy istnieją trójki liczb pierwszych, takie że pierwsza jest oddzielona
od drugiej przez jedną liczbę złożoną i druga od trzeciej tak samo? Czytelnik
Spostrzegawczy wymieni od razu liczby 3, 5 i 7. Okazuje się jednak, że jest to
jedyny przykład „trojaczków”. Żeby się o tym przekonać, wystarczy
zauważyć, że liczby
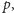
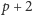 i
i
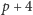 dają różne reszty
z dzielenia przez 3. Ponieważ mamy tylko trzy możliwe reszty do dyspozycji,
to jedna z nich musi być zerem, czyli jedna z liczb
dają różne reszty
z dzielenia przez 3. Ponieważ mamy tylko trzy możliwe reszty do dyspozycji,
to jedna z nich musi być zerem, czyli jedna z liczb
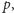

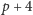 jest podzielna przez 3. Wobec tego, jeśli żądamy, żeby te liczby
były pierwsze, to wśród nich musi wystąpić 3. To oznacza, że nie ma
innych możliwości poza układem 3, 5 i 7.
jest podzielna przez 3. Wobec tego, jeśli żądamy, żeby te liczby
były pierwsze, to wśród nich musi wystąpić 3. To oznacza, że nie ma
innych możliwości poza układem 3, 5 i 7.
Nie umiemy na razie rozstrzygnąć, ile jest par liczb pierwszych leżących
możliwie blisko, ale wiadomo, że przerwy między kolejnymi liczbami
pierwszymi mogą być dowolnie długie. Żeby się o tym przekonać,
wystarczy podać metodę konstrukcji ciągu
 kolejnych liczb
złożonych dla
kolejnych liczb
złożonych dla
 będącego dowolną liczbą naturalną. A ten ciąg
wygląda tak:
będącego dowolną liczbą naturalną. A ten ciąg
wygląda tak:

– kolejne liczby dzielą się przez
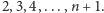
Wreszcie, liczby pierwsze mają zastosowanie praktyczne. Na nich opierają się
algorytmy szyfrujące, używane obecnie do zabezpieczania naprawdę ważnych
rzeczy. Taki jest algorytm RSA, który jest przykładem szyfru z kluczem
publicznym: powszechnie dostępne są dane pozwalające zaszyfrować
wiadomość, ale odszyfrować ją można tylko znając drugą, prywatną
część klucza. Żeby stworzyć taką parę złożoną z klucza publicznego
i prywatnego, trzeba zacząć od dwóch odpowiednio dużych liczb
pierwszych
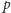 i
i
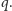 Bierzemy ich iloczyn
Bierzemy ich iloczyn
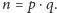 Liczba
Liczba
 wraz z innymi informacjami stanowi klucz publiczny. Natomiast liczby
wraz z innymi informacjami stanowi klucz publiczny. Natomiast liczby
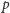 i
i
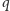 zostają utajnione – będą częścią klucza prywatnego, bez
nich nie uda się odczytać zaszyfrowanej wiadomości. Okazuje się, iż
bezpieczeństwo tego szyfru wynika z faktu, że rozkładanie liczb na
czynniki pierwsze ogólnie jest trudnym problemem. Dokładniej, jeśli
znamy
zostają utajnione – będą częścią klucza prywatnego, bez
nich nie uda się odczytać zaszyfrowanej wiadomości. Okazuje się, iż
bezpieczeństwo tego szyfru wynika z faktu, że rozkładanie liczb na
czynniki pierwsze ogólnie jest trudnym problemem. Dokładniej, jeśli
znamy
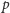 i
i
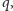 to łatwo obliczamy ich iloczyn
to łatwo obliczamy ich iloczyn
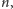 ale
jeśli znamy tylko
ale
jeśli znamy tylko
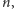 to możemy mieć problem z odtworzeniem
wartości
to możemy mieć problem z odtworzeniem
wartości
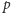 i
i
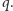 Oczywiście, nie w takich przypadkach, gdy
liczby są niezbyt wielkie, jak na przykład
Oczywiście, nie w takich przypadkach, gdy
liczby są niezbyt wielkie, jak na przykład
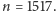 Tutaj komputer
w ułamku sekundy, a Czytelnik w kilka minut sprawdzi, że
Tutaj komputer
w ułamku sekundy, a Czytelnik w kilka minut sprawdzi, że
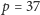 i
i
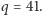 Ale jeśli liczby
Ale jeśli liczby
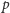 i
i
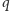 mają ponad 200 cyfr
długości... Trzeba jednak wziąć pod uwagę ciągły rozwój algorytmów
i sprzętu komputerowego. Te problemy obliczeniowe, których obecne
komputery nie rozwiążą w sensownym czasie, za kilka lat mogą okazać się
łatwiejsze – być może powstanie nowy algorytm rozwiązujący problem
istotnie szybciej, a być może nowe parametry komputerów wystarczą do
wykonania pewnych obliczeń. Wobec tego ciągle potrzebne są nowe
liczby pierwsze, za każdym razem trochę większe niż wcześniej.
Chcielibyśmy więc wiedzieć, jak szukać liczb pierwszych i jak sprawdzić,
czy dana liczba jest pierwsza. Algorytmy używane obecnie do znajdowania
liczb pierwszych i testowania pierwszości to temat na inną, dłuższą
opowieść. Spróbujemy więc przyjrzeć się temu, jak dawniej szukano liczb
pierwszych.
mają ponad 200 cyfr
długości... Trzeba jednak wziąć pod uwagę ciągły rozwój algorytmów
i sprzętu komputerowego. Te problemy obliczeniowe, których obecne
komputery nie rozwiążą w sensownym czasie, za kilka lat mogą okazać się
łatwiejsze – być może powstanie nowy algorytm rozwiązujący problem
istotnie szybciej, a być może nowe parametry komputerów wystarczą do
wykonania pewnych obliczeń. Wobec tego ciągle potrzebne są nowe
liczby pierwsze, za każdym razem trochę większe niż wcześniej.
Chcielibyśmy więc wiedzieć, jak szukać liczb pierwszych i jak sprawdzić,
czy dana liczba jest pierwsza. Algorytmy używane obecnie do znajdowania
liczb pierwszych i testowania pierwszości to temat na inną, dłuższą
opowieść. Spróbujemy więc przyjrzeć się temu, jak dawniej szukano liczb
pierwszych.
Przypomnijmy najpierw dowód, że liczb pierwszych jest nieskończenie
wiele. Załóżmy przeciwnie, że jest ich skończenie wiele, a dokładnie
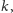 i ponumerujmy je:
i ponumerujmy je:
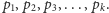 Popatrzmy teraz na iloczyn
tych liczb i dodajmy do niego jedynkę:
Popatrzmy teraz na iloczyn
tych liczb i dodajmy do niego jedynkę:

Czy liczba
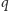 jest pierwsza, czy złożona?
jest pierwsza, czy złożona?
Okazuje się, że żadna z tych możliwości nie może mieć miejsca:
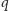 nie jest pierwsza, bo jest różna od każdej z liczb
nie jest pierwsza, bo jest różna od każdej z liczb
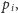 nie jest
też złożona, bo nie dzieli się przez żadną z liczb pierwszych
nie jest
też złożona, bo nie dzieli się przez żadną z liczb pierwszych
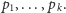 Nie może więc istnieć, a skoro istnieje, oznacza to, że
zbudowaliśmy ją, korzystając z błędnego założenia – jedynym założeniem
było zaś istnienie tylko skończonej liczby liczb pierwszych. Trzeba więc z niego
zrezygnować.
Nie może więc istnieć, a skoro istnieje, oznacza to, że
zbudowaliśmy ją, korzystając z błędnego założenia – jedynym założeniem
było zaś istnienie tylko skończonej liczby liczb pierwszych. Trzeba więc z niego
zrezygnować.
Mogłoby się wydawać, że ten dowód podsuwa nam pomysł, jak wyznaczać
coraz większe liczby pierwsze: wystarczy wziąć wszystkie liczby pierwsze
mniejsze od danej liczby, wymnożyć je, dodać jeden i
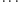 Zaraz, czy na
pewno ta liczba nie jest złożona? Patrząc na przykłady małych liczb, wydaje się,
że ten pomysł działa dobrze:
Zaraz, czy na
pewno ta liczba nie jest złożona? Patrząc na przykłady małych liczb, wydaje się,
że ten pomysł działa dobrze:

– wszystkie wyniki są liczbami pierwszymi.
Ale już dla sześciu początkowych liczb pierwszych dostajemy

Czyli w naszym rozumowaniu musi być coś niepoprawnego. Zwróćmy uwagę na to, że w podanym dowodzie wszystko robiliśmy przy założeniu, że liczb pierwszych jest skończenie wiele. W szczególności obserwację, że liczba

nie może być złożona, otrzymaliśmy, zakładając, że wymnożyliśmy wszystkie istniejące liczby pierwsze. Tymczasem mogą istnieć liczby pierwsze większe od każdej z wymnażanych, ale mniejsze od ich iloczynu – tutaj takimi liczbami są, na przykład, 17, 29, czy właśnie 59.
Istnieją inne wzory, których matematycy używali do znajdowania dobrych
kandydatów na liczby pierwsze. Na przykład Marin Mersenne badał liczby
postaci
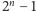 i znajdował wśród nich liczby pierwsze, wiedząc, że taka
liczba może być pierwsza tylko wtedy, gdy wykładnik
i znajdował wśród nich liczby pierwsze, wiedząc, że taka
liczba może być pierwsza tylko wtedy, gdy wykładnik
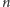 jest liczbą
pierwszą. Na liczbach tej postaci bardzo dobrze działają niektóre testy
pierwszości, więc znane są obecnie bardzo duże liczby pierwsze Mersenne’a.
Aktualny rekord (prawie 13 milionów cyfr) to
jest liczbą
pierwszą. Na liczbach tej postaci bardzo dobrze działają niektóre testy
pierwszości, więc znane są obecnie bardzo duże liczby pierwsze Mersenne’a.
Aktualny rekord (prawie 13 milionów cyfr) to
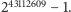 Wyniki
testów pierwszości dla tej liczby otrzymano w sierpniu 2008 roku i od tego
czasu nie udało się trafić na żadną większą liczbę pierwszą Mersenne’a.
Nie wiadomo nawet, czy jest ich nieskończenie wiele. Wiemy natomiast, że
wśród liczb postaci
Wyniki
testów pierwszości dla tej liczby otrzymano w sierpniu 2008 roku i od tego
czasu nie udało się trafić na żadną większą liczbę pierwszą Mersenne’a.
Nie wiadomo nawet, czy jest ich nieskończenie wiele. Wiemy natomiast, że
wśród liczb postaci
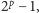 gdzie
gdzie
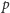 to liczba pierwsza, istnieje
nieskończenie wiele liczb złożonych.
to liczba pierwsza, istnieje
nieskończenie wiele liczb złożonych.
Pierre Fermat z kolei zajmował się liczbami postaci
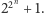 Po sprawdzeniu
pierwszości pięciu początkowych wyrazów tego ciągu (liczymy od
Po sprawdzeniu
pierwszości pięciu początkowych wyrazów tego ciągu (liczymy od
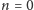 )
postawił nawet hipotezę, że wszystkie liczby opisane tym wzorem są
pierwsze. Jednak szósta z tych liczb,
)
postawił nawet hipotezę, że wszystkie liczby opisane tym wzorem są
pierwsze. Jednak szósta z tych liczb,
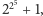 jest już złożona, ale
Fermatowi nie udało się rozłożyć jej na czynniki pierwsze. Co ciekawe,
pewien rozkład szóstej liczby Fermata można znaleźć za pomocą
łatwych przekształceń arytmetycznych – trzeba tylko umieć dobrze
zgadywać.
jest już złożona, ale
Fermatowi nie udało się rozłożyć jej na czynniki pierwsze. Co ciekawe,
pewien rozkład szóstej liczby Fermata można znaleźć za pomocą
łatwych przekształceń arytmetycznych – trzeba tylko umieć dobrze
zgadywać.

Widać, że to już koniec? Wystarczy zauważyć, że

Zatem

Jak widać, rozstrzygnięcie tej hipotezy z pewnością leżało w zasięgu możliwości Fermata. Natomiast w zasięgu naszych możliwości do tej chwili nie leży rozstrzygnięcie, czy istnieją jeszcze inne liczby pierwsze Fermata, poza wymienionymi przez niego, czyli 3, 5, 17, 257 i 65537.
Później Leonard Euler poszukiwał liczb pierwszych wśród wartości
pewnych wielomianów. Znalazł funkcję
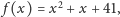 która po
podstawieniu liczb z zakresu od 0 do 39 daje w wyniku liczby pierwsze. Jak
łatwo sprawdzić, dla
która po
podstawieniu liczb z zakresu od 0 do 39 daje w wyniku liczby pierwsze. Jak
łatwo sprawdzić, dla
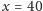 otrzymujemy już liczbę złożoną. A czy
istnieją inne wielomiany postaci
otrzymujemy już liczbę złożoną. A czy
istnieją inne wielomiany postaci
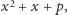 gdzie
gdzie
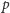 jest
pierwsza, o tej własności, że dla liczb od 0 do
jest
pierwsza, o tej własności, że dla liczb od 0 do
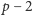 dają w wyniku
liczbę pierwszą? [Odpowiedź]
dają w wyniku
liczbę pierwszą? [Odpowiedź]
W czasach Eulera powstała także piękna hipoteza, nierozstrzygnięta do dzisiaj. Christian Goldbach zauważył, że wiele liczb parzystych można przedstawić w postaci sumy dwóch liczb pierwszych (niekoniecznie różnych). Co więcej, nie znalazł przykładu liczby parzystej, której nie dałoby się zapisać w ten sposób (oprócz 2, która po prostu jest za mała). Postawił więc hipotezę, że każda liczba parzysta większa od 2 jest sumą dwóch liczb pierwszych. Prostota sformułowania jest, niestety, złudna.
Przez ponad 250 lat, używając zarówno „tradycyjnych” metod matematycznych,
jak i programów komputerowych, matematycy nie zdołali udowodnić ani
obalić tej hipotezy. Sprawdzono ją jednak, oczywiście za pomocą metod
komputerowych, dla liczb parzystych mniejszych od
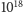 – umiemy
przedstawić te liczby jako sumy dwóch liczb pierwszych. Te wyniki
obliczeniowe skłaniają matematyków do wiary w prawdziwość hipotezy
Goldbacha, ale dopóki nie będzie dowodu, nigdy nie wiadomo, co może
się zdarzyć.
– umiemy
przedstawić te liczby jako sumy dwóch liczb pierwszych. Te wyniki
obliczeniowe skłaniają matematyków do wiary w prawdziwość hipotezy
Goldbacha, ale dopóki nie będzie dowodu, nigdy nie wiadomo, co może
się zdarzyć.
A co z liczbami nieparzystymi? Tak zwana słaba hipoteza Goldbacha mówi, że każdą liczbę nieparzystą większą niż 5 można przedstawić jako sumę trzech liczb pierwszych. Czytelnik Wnikliwy sprawdzi, że słaba hipoteza faktycznie wynika z tej dla liczb parzystych. Niestety, słabszej wersji także, jak dotąd, nie udało się rozstrzygnąć.
Na koniec – wracając do problemów, które powinny przynieść Czytelnikom więcej radości niż frustracji – zagadka. 30 jest największą liczbą, dla której wszystkie mniejsze od niej i względnie pierwsze z nią są liczbami pierwszymi. Jakie są inne takie liczby i dlaczego nie ma większych?
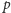 jest taką liczbą, to można cyrklem i linijką
skonstruować
jest taką liczbą, to można cyrklem i linijką
skonstruować
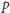 -kąt foremny, a Pierre Wanzel – że dla żadnej innej
liczby pierwszej taka konstrukcja nie jest możliwa.
-kąt foremny, a Pierre Wanzel – że dla żadnej innej
liczby pierwszej taka konstrukcja nie jest możliwa.
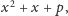 gdzie
gdzie
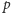 jest liczbą pierwszą,
mających tę własność, że dla wartości
jest liczbą pierwszą,
mających tę własność, że dla wartości
 z zakresu od 0 do
z zakresu od 0 do
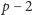 przyjmują wartości będące liczbami pierwszymi, wcale
nie jest dużo. Euler w 1772 roku, oprócz wspomnianego w Małej Delcie
przyjmują wartości będące liczbami pierwszymi, wcale
nie jest dużo. Euler w 1772 roku, oprócz wspomnianego w Małej Delcie
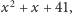 znał jeszcze cztery wielomiany tego typu:
znał jeszcze cztery wielomiany tego typu:

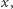 dla których wielomian daje w wyniku
liczbę pierwszą, kończą się na
dla których wielomian daje w wyniku
liczbę pierwszą, kończą się na
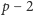 ? Dla
? Dla
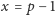 mamy
mamy