Drobiazgi
O niespodziewanej tożsamości algebraicznej
Załóżmy, że suma kw adratów trzech liczb naturalnych jest podwojonym kwadratem pewnej liczby naturalnej. Czy możliwe jest, żeby wówczas suma czwartych potęg tych trzech liczb była podwojoną czwartą potęgą tej samej liczby?
Okazuje się, że może tak być. Powiemy, jak skonstruować nieskończenie wiele takich trójek w szczególnym przypadku, gdy jedna z tych trzech liczb jest sumą dwóch pozostałych.
Zauważmy najpierw, że

W szczególności, gdy weźmiemy
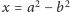 oraz
oraz
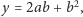 a zatem
a zatem
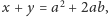 otrzymujemy właśnie
otrzymujemy właśnie

Na przykład dla
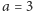 i
i
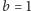 mamy
mamy

Czy badana zależność jest spełniona tylko wtedy, gdy jedna z trzech liczb jest sumą dwóch pozostałych? Czy skonstruowaliśmy wszystkie trójki liczb naturalnych spełniające tę zależność? Pozostawiam to do przemyślenia Czytelnikom.