Mała Delta
Jak znaleźć klucz?
Każdy od czasu do czasu potrzebuje metody przekazania komuś pewnych wiadomości tak, żeby niepowołane osoby nie miały szans na ich przechwycenie. Począwszy od zabaw z kolegami na podwórku, a skończywszy na operacjach bankowych, wojskowych czy wykorzystujących dane osobowe – bez szyfrów po prostu nie da się żyć. Do zaszyfrowania danych zwykle potrzebny jest klucz – pewne słowo czy liczba, które najpierw kierują procesem tworzenia szyfru, a później pozwalają odbiorcy wiadomości ją odkodować. Osoby, które chcą porozumiewać się za pomocą szyfru, muszą najpierw uzgodnić klucz między sobą. I tu pojawia się problem: jak ustalić klucz, tak żeby nikt oprócz nas nie mógł go poznać?
Można się w tym celu spotkać, ale każdy, kto oglądał filmy szpiegowskie, wie, jak łatwo jest podsłuchać rozmowę. Wysłanie klucza pocztą, wszystko jedno, czy papierową, czy elektroniczną, to pomysł tak samo skazany na porażkę. A gdyby wysłać klucz w formie zaszyfrowanej? Trzeba by najpierw ustalić klucz do szyfru, którym zaszyfrujemy klucz do tego szyfru, którego chcemy używać w korespondencji, czyli wróciliśmy do początkowego problemu... Nie załamujmy się jednak: banki mają się całkiem dobrze (co wyraźnie widać z szyldów lokali użytkowych), tajemnice wojskowe raczej też, i chociaż parę miesięcy temu pewna firma miała duże kłopoty z wyciekiem danych użytkowników konsoli do gier, to jednak ogólny obraz sytuacji wskazuje na to, że istnieją dobre metody zabezpieczania informacji.
Zobaczmy więc, jak ustalić klucz do szyfru w taki sposób, żeby szanse na poznanie go przez osoby niepowołane były bardzo, bardzo małe. Zacznijmy od tego, że ustalanie klucza będzie się odbywać publicznie – osoby A i B, które ten klucz ustalają, wszystkie informacje, które muszą wymienić, mogą ogłosić wszem i wobec. To oznacza, że przy tej metodzie problem podsłuchu nie istnieje. Metoda jest tak opracowana, żeby osoba, która usłyszy wszystkie informacje wymieniane przez osoby A i B, nie mogła odgadnąć ustalonego klucza. Powiesz, Czytelniku, że to niemożliwe? Sprawdźmy!
Będziemy potrzebowali operacji modulo, która daje resztę z dzielenia jednej liczby
przez drugą. Zapis
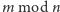 oznacza resztę z dzielenia
oznacza resztę z dzielenia
 przez
przez
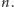 Na przykład
Na przykład
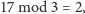 a
a
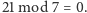 W ten
sposób możemy łatwo przerobić dowolną liczbę całkowitą na liczbę z zakresu
od 0 do
W ten
sposób możemy łatwo przerobić dowolną liczbę całkowitą na liczbę z zakresu
od 0 do
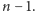 Niech teraz
Niech teraz
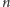 oznacza pewną dużą liczbę, a
oznacza pewną dużą liczbę, a
 będzie pewną liczbą dodatnią mniejszą niż
będzie pewną liczbą dodatnią mniejszą niż
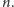 Osoby A i B
uzgadniają tę parę liczb, nie ukrywając ich przed światem. Następnie
wybierają jeszcze dwie liczby, ale tym razem tajne. Osoba A wymyśla liczbę
Osoby A i B
uzgadniają tę parę liczb, nie ukrywając ich przed światem. Następnie
wybierają jeszcze dwie liczby, ale tym razem tajne. Osoba A wymyśla liczbę
 z zakresu od 0 do
z zakresu od 0 do
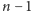 i nikomu o niej nie mówi; tak samo
osoba B wybiera liczbę
i nikomu o niej nie mówi; tak samo
osoba B wybiera liczbę
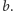 Następnym krokiem jest wykonanie
potęgowania. Osoba A oblicza wartość
Następnym krokiem jest wykonanie
potęgowania. Osoba A oblicza wartość

i ją udostępnia. Analogicznie, osoba B oblicza i udostępnia

Kolejne obliczenie pozwala już otrzymać klucz. Osoba A bierze wartość
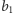 obliczoną przez osobę B, podnosi do potęgi
obliczoną przez osobę B, podnosi do potęgi
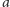 i wykonuje na
wyniku operację
i wykonuje na
wyniku operację
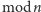 :
:

(Sprawdź dokładnie, Czytelniku, dlaczego końcowa równość jest prawdziwa.) Osoba B oblicza

czyli obie osoby otrzymały tę samą wartość
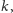 która będzie ich
tajnym kluczem do szyfru. Ta procedura uzgadniania klucza to protokół
Diffiego–Hellmana.
która będzie ich
tajnym kluczem do szyfru. Ta procedura uzgadniania klucza to protokół
Diffiego–Hellmana.
A co wie osoba z zewnątrz, która chciałaby odgadnąć klucz i złamać szyfr?
Otóż, wbrew pozorom, bardzo niewiele. Publicznie zostały podane wartości
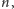
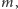
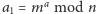 i
i
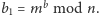 Żeby
odtworzyć klucz, potrzebna jest znajomość liczby
Żeby
odtworzyć klucz, potrzebna jest znajomość liczby
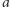 lub
lub
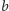 – mając
jedną z tych liczb, osoba podsłuchująca może przeprowadzić takie obliczenie,
jak osoby A i B pod koniec ustaleń. Problem sprowadza się więc do pytania, czy
znajomość liczb
– mając
jedną z tych liczb, osoba podsłuchująca może przeprowadzić takie obliczenie,
jak osoby A i B pod koniec ustaleń. Problem sprowadza się więc do pytania, czy
znajomość liczb
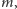
 i
i
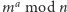 wystarcza do
wyznaczenia liczby
wystarcza do
wyznaczenia liczby
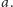 Okazuje się, że ogólnie nie wystarcza, czyli
można dobrać liczby
Okazuje się, że ogólnie nie wystarcza, czyli
można dobrać liczby
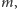
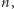
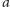 i
i
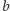 w taki
sposób, żeby odgadnięcie klucza przez osobę z zewnątrz było praktycznie
niemożliwe przy naszym obecnym stanie wiedzy. Oczywiście, może
się zdarzyć, że za kilka lat powstaną algorytmy i programy radzące
sobie świetnie z tym problemem, ale na razie opisane metody można
z powodzeniem stosować.
w taki
sposób, żeby odgadnięcie klucza przez osobę z zewnątrz było praktycznie
niemożliwe przy naszym obecnym stanie wiedzy. Oczywiście, może
się zdarzyć, że za kilka lat powstaną algorytmy i programy radzące
sobie świetnie z tym problemem, ale na razie opisane metody można
z powodzeniem stosować.
Problem odtworzenia liczby
 z liczb
z liczb
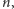
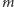 i
i
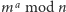 nazywa się problemem logarytmu dyskretnego. Szukając
wartości
nazywa się problemem logarytmu dyskretnego. Szukając
wartości
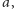 próbujemy wykonać operację odwrotną do potęgowania
modulo
próbujemy wykonać operację odwrotną do potęgowania
modulo
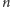 i stąd logarytm w nazwie. Potęgowanie modulo
i stąd logarytm w nazwie. Potęgowanie modulo
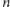 jest
tak zwaną funkcją jednokierunkową – samą potęgę można obliczyć
łatwo i szybko, ale odwrócenie tej operacji jest dla nas (na razie) bardzo
trudnym problemem obliczeniowym. Tak trudnym, że dla odpowiedniego
doboru danych (potrzebne są naprawdę duże, kilkusetcyfrowe liczby)
uznaje się go właściwie za niewykonalny i jego trudności powierza się
ważne tajemnice.
jest
tak zwaną funkcją jednokierunkową – samą potęgę można obliczyć
łatwo i szybko, ale odwrócenie tej operacji jest dla nas (na razie) bardzo
trudnym problemem obliczeniowym. Tak trudnym, że dla odpowiedniego
doboru danych (potrzebne są naprawdę duże, kilkusetcyfrowe liczby)
uznaje się go właściwie za niewykonalny i jego trudności powierza się
ważne tajemnice.