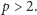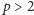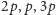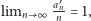Ciąg EKG, czyli zaskakująca zabawa z teorią liczb
Teoria liczb w wielu miejscach jest zaskakująca i nieprzewidywalna, co – na poziomie elementarnym – objawia się przede wszystkim przez nieregularne i trudne do opisania rozmieszczenie liczb pierwszych w zbiorze liczb naturalnych. Wraz z Piotrem Hofmanem zmierzyliśmy się z tym fenomenem, badając tzw. ciąg EKG: prosty do zdefiniowania, a z bardzo ciekawymi właściwościami.
Ciąg EKG
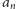 określamy następująco:
określamy następująco:
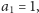
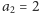 i dalej
i dalej
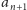 jest najmniejszą liczbą całkowitą dodatnią niewystępującą wcześniej
w ciągu, taką że
jest najmniejszą liczbą całkowitą dodatnią niewystępującą wcześniej
w ciągu, taką że
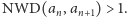 Jako pierwszy zajmował się tym
ciągiem Ayres, następnie badali go Lagarias, Rains i Sloane.
Jako pierwszy zajmował się tym
ciągiem Ayres, następnie badali go Lagarias, Rains i Sloane.
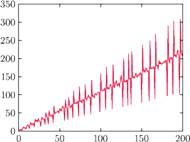
Rys. 1 Pierwsze 200 wyrazów ciągu EKG
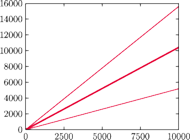
Rys. 1 Pierwsze 10000 wyrazów ciągu EKG
Skąd nazwa ciąg EKG? Pierwsze
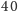 wyrazów ciągu nam może tego
nie powie:
wyrazów ciągu nam może tego
nie powie:

 wyrazów (Rys. 1), to
zobaczymy coś ciekawego. Nasuwa się pytanie: czemu zawdzięczamy te „skoki”
na wykresie, przypominające zachowanie elektrokardiogramu? Prześledzenie
wyrazów ciągu EKG pokazuje, że te skoki to trójki kolejnych wyrazów
postaci
wyrazów (Rys. 1), to
zobaczymy coś ciekawego. Nasuwa się pytanie: czemu zawdzięczamy te „skoki”
na wykresie, przypominające zachowanie elektrokardiogramu? Prześledzenie
wyrazów ciągu EKG pokazuje, że te skoki to trójki kolejnych wyrazów
postaci
 dla liczb pierwszych
dla liczb pierwszych
 Lagarias, Rains
i Sloane wykazali, między innymi, że ciąg
Lagarias, Rains
i Sloane wykazali, między innymi, że ciąg
 jest permutacją
liczb całkowitych dodatnich, że liczby pierwsze pojawiają się w nim
w kolejności rosnącej i że asymptotycznie zachowuje się on liniowo
(dokładniej,
jest permutacją
liczb całkowitych dodatnich, że liczby pierwsze pojawiają się w nim
w kolejności rosnącej i że asymptotycznie zachowuje się on liniowo
(dokładniej,
 dla każdego
dla każdego
 ). Rysunek 2,
pokazujący pierwszych
). Rysunek 2,
pokazujący pierwszych
 wyrazów ciągu EKG, sugeruje, że
powinniśmy potrafić udowodnić dużo dokładniejsze ograniczenia: poza
skokami,
wyrazów ciągu EKG, sugeruje, że
powinniśmy potrafić udowodnić dużo dokładniejsze ograniczenia: poza
skokami,
 jest równe prawie dokładnie
jest równe prawie dokładnie
 Oznaczmy
Oznaczmy
 jeśli
jeśli
 lub
lub
 dla liczby pierwszej
dla liczby pierwszej
 i
i
 w przeciwnym przypadku. Ta definicja
„łagodzi” skoki. Spodziewamy się więc, że będzie
w przeciwnym przypadku. Ta definicja
„łagodzi” skoki. Spodziewamy się więc, że będzie
 tj.
tj.
 Bazując na eksperymentach numerycznych, Lagarias,
Rains i Sloane postawili następujące hipotezy:
Bazując na eksperymentach numerycznych, Lagarias,
Rains i Sloane postawili następujące hipotezy:
Wraz z Piotrem Hofmanem udowodniliśmy pierwszą hipotezę
i częściowo drugą: wykazaliśmy, że istnieje taka stała uniwersalna
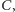 że
że

co oczywiście implikuje
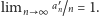 Dowód powyższego
oszacowania jest żmudny i wymaga wielu drobnych technicznych kroków.
Za to dowód pierwszej hipotezy jest dość krótki i przedstawię go w dalszej
części artykułu.
Dowód powyższego
oszacowania jest żmudny i wymaga wielu drobnych technicznych kroków.
Za to dowód pierwszej hipotezy jest dość krótki i przedstawię go w dalszej
części artykułu.

Dowód hipotezy 1. Jeśli
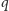 jest liczbą pierwszą dzielącą zarówno
jest liczbą pierwszą dzielącą zarówno
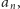 jak i
jak i
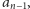 to
to
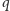 nazywamy liczbą sterującą wyrazu
nazywamy liczbą sterującą wyrazu
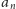 (to nie jest definicja jednoznaczna, dla jednego
(to nie jest definicja jednoznaczna, dla jednego
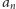 możemy
mieć wiele liczb sterujących). Zauważmy, że
możemy
mieć wiele liczb sterujących). Zauważmy, że
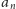 jest najmniejszą liczbą
niewystępującą wcześniej w ciągu, a podzielną przez
jest najmniejszą liczbą
niewystępującą wcześniej w ciągu, a podzielną przez
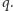 Kluczowe jest
następujące spostrzeżenie. Ustalmy liczbę rzeczywistą
Kluczowe jest
następujące spostrzeżenie. Ustalmy liczbę rzeczywistą
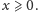 Wówczas,
dla każdej liczby pierwszej
Wówczas,
dla każdej liczby pierwszej
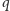 istnieje co najwyżej jeden taki wyraz
ciągu
istnieje co najwyżej jeden taki wyraz
ciągu
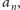 że
że
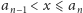 i
i
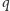 jest liczbą sterującą
jest liczbą sterującą
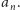 Istotnie, zauważmy, iż jeśli
Istotnie, zauważmy, iż jeśli
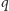 jest liczbą sterującą
jest liczbą sterującą
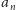 i
i
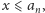 to wszystkie liczby mniejsze od
to wszystkie liczby mniejsze od
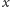 podzielne
przez
podzielne
przez
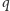 wystąpiły wcześniej w ciągu. Czyli jeśli dla pewnego
wystąpiły wcześniej w ciągu. Czyli jeśli dla pewnego
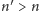 mamy
mamy
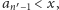 to
to
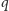 nie dzieli
nie dzieli
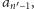 a więc
nie może być liczbą sterującą
a więc
nie może być liczbą sterującą
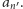 Załóżmy, że pewna liczba
pierwsza
Załóżmy, że pewna liczba
pierwsza
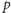 pojawia się w ciągu niepoprzedzona wyrazem
pojawia się w ciągu niepoprzedzona wyrazem
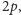 czyli
czyli
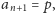
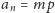 dla pewnych całkowitych
dla pewnych całkowitych
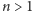 i
i
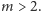 Lagarias, Rains i Sloane udowodnili, że wówczas
Lagarias, Rains i Sloane udowodnili, że wówczas
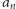 jest
pierwszym wyrazem ciągu podzielnym przez
jest
pierwszym wyrazem ciągu podzielnym przez
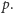 W szczególności
oznacza to, że
W szczególności
oznacza to, że
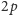 nie wystąpiło w ciągu przed pozycją
nie wystąpiło w ciągu przed pozycją

Rozpatrzmy zbiory

Zauważmy, że
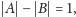 gdyż
gdyż
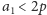 i
i
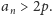 Doprowadzimy do sprzeczności, dowodząc, że jeśli
Doprowadzimy do sprzeczności, dowodząc, że jeśli
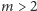 i
i
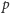 jest wystarczająco duże, to zbiór
jest wystarczająco duże, to zbiór
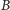 jest dużo
większy niż
jest dużo
większy niż
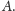 Jak wykazali Lagarias, Rains i Sloane, liczby pierwsze
pojawiają się w ciągu EKG w kolejności rosnącej, czyli przed pozycją
Jak wykazali Lagarias, Rains i Sloane, liczby pierwsze
pojawiają się w ciągu EKG w kolejności rosnącej, czyli przed pozycją
 nie pojawiła się liczba pierwsza większa niż
nie pojawiła się liczba pierwsza większa niż
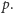 Jeśli
Jeśli
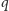 jest liczbą sterującą wyrazu
jest liczbą sterującą wyrazu
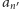 i
i
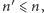 to
to
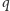 jest
kandydatem na wyraz
jest
kandydatem na wyraz
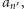 więc pojawia się w ciągu na pozycji
więc pojawia się w ciągu na pozycji
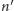 lub wcześniejszej. Wnioskujemy stąd, że wszystkie liczby
sterujące do pozycji
lub wcześniejszej. Wnioskujemy stąd, że wszystkie liczby
sterujące do pozycji
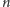 są mniejsze niż
są mniejsze niż
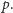 Z podanego
przed chwilą „kluczowego spostrzeżenia” wiemy, że dla każdej liczby
pierwszej
Z podanego
przed chwilą „kluczowego spostrzeżenia” wiemy, że dla każdej liczby
pierwszej
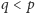 istnieje co najwyżej jeden taki indeks
istnieje co najwyżej jeden taki indeks
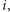 że
że
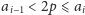 i
i
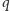 jest liczbą sterującą
jest liczbą sterującą
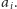 Liczb pierwszych
nie większych niż
Liczb pierwszych
nie większych niż
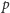 jest nie więcej niż
jest nie więcej niż
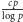 dla pewnej stałej
uniwersalnej
dla pewnej stałej
uniwersalnej
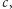 czyli
czyli

Spójrzmy teraz na zbiór
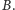 Niech
Niech
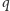 będzie liczbą sterującą
wyrazu
będzie liczbą sterującą
wyrazu
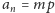 ; oczywiście
; oczywiście
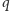 jest dzielnikiem
jest dzielnikiem
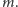 Wobec
tego liczby
Wobec
tego liczby
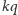 dla
dla
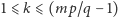 musiały pojawić się w ciągu
wcześniej. Oznaczmy
musiały pojawić się w ciągu
wcześniej. Oznaczmy

Indeksy wszystkich parzystych wyrazów postaci
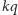 (podzielnych przez 4,
jeśli
(podzielnych przez 4,
jeśli
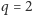 ), większych od
), większych od
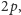 należą do
należą do
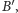 wobec
tego
wobec
tego

Z drugiej strony, jeśli
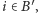 to
to
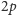 jest potencjalnym
kandydatem na wyraz
jest potencjalnym
kandydatem na wyraz
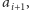 czyli
czyli
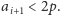 Mamy więc
Mamy więc
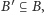 zatem
zatem

Wobec tego dla odpowiednio dużych
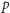 mamy
mamy
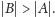 Wyliczywszy
dokładnie stałe w powyższym rozumowaniu, można dowieść, że
Wyliczywszy
dokładnie stałe w powyższym rozumowaniu, można dowieść, że
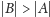 już dla
już dla
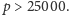 Teza dla mniejszych wartości
Teza dla mniejszych wartości
 została sprawdzona numerycznie przez Lagariasa, Rainsa i Sloane’a,
więc hipoteza została udowodniona dla wszystkich
została sprawdzona numerycznie przez Lagariasa, Rainsa i Sloane’a,
więc hipoteza została udowodniona dla wszystkich