Spacerujący matematyk
Gdy odbywam długie spacery, pewien fakt nieustannie zwraca moją uwagę. O ile zachowuję stałą długość kroku, wciąż zdarza się, że następuję na linie oddzielające kolejne płyty chodnika. Dlaczego tak się dzieje?
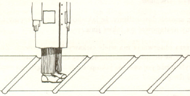
Spróbujmy sformułować powyższe zagadnienie jako problem matematyczny.
Załóżmy, że chodnik jest zbudowany z płyt w kształcie prostokątów,
każdy o długości 1 m. Kolejne płyty są oddzielone wąskimi przerwami. Aby
podkreślić fakt, że przerwy są rzeczywiście wąskie, ich szerokość
oznaczymy przez
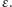 Załóżmy teź, że przed rozpoczęciem spaceru
stoję w ten sposób, iż czubki moich butów dotykają przerwy między płytami.
Aby uniknąć niejednoznaczności w definicji „następowania na linię”,
wyrażę ją w ścisły sposób: następuję na linię tylko wtedy, gdy czubek
mojego buta dotyka jednej z przerw o szerokości
Załóżmy teź, że przed rozpoczęciem spaceru
stoję w ten sposób, iż czubki moich butów dotykają przerwy między płytami.
Aby uniknąć niejednoznaczności w definicji „następowania na linię”,
wyrażę ją w ścisły sposób: następuję na linię tylko wtedy, gdy czubek
mojego buta dotyka jednej z przerw o szerokości
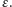 Pytanie: czy
mogę tak dobrać długość
Pytanie: czy
mogę tak dobrać długość
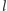 mojego kroku, aby nie następować
na linie?
mojego kroku, aby nie następować
na linie?
Oczywiście,
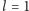 jest wyborem najgorszym z możliwych: w tej sytuacji
następuję na każdą linię. Większe liczby naturalne wcale nie są lepsze:
w każdym kroku będę następował na linię. Żadna z liczb wymiernych nie jest
również dobrym wyborem: gdy będzie to
jest wyborem najgorszym z możliwych: w tej sytuacji
następuję na każdą linię. Większe liczby naturalne wcale nie są lepsze:
w każdym kroku będę następował na linię. Żadna z liczb wymiernych nie jest
również dobrym wyborem: gdy będzie to
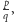 po każdych
po każdych
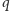 krokach również powtarza się poprzedni przypadek. A co stanie się, gdy
wybiorę
krokach również powtarza się poprzedni przypadek. A co stanie się, gdy
wybiorę
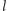 niewymierne, np.
niewymierne, np.
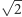 ?
?
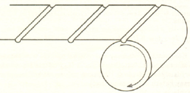
Aby uprościć rozważania, wyobraźmy sobie, że chodnik zwinęliśmy jak dywan.
Teraz wygląda on jak okrąg, w którym wszystkie przerwy zajmują tę samą
pozycję na obwodzie. Zaczynamy spacer. W czasie drogi zaznaczamy na okręgu
kolejne ślady
 czubków butów.
czubków butów.
Teraz robimy tak. Wybieramy liczbę naturalną
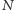 spełniającą warunek
spełniającą warunek
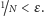 Dzielimy obwód naszego okręgu na
Dzielimy obwód naszego okręgu na
 równych łuków,
każdy o długości
równych łuków,
każdy o długości
 m.
m.
Ponieważ liczby
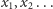 są niewymierne, żadna z nich nie
wypadnie na punkcie podziału. Jak wynika z zasady szufladkowej Dirichleta,
istnieją punkty
są niewymierne, żadna z nich nie
wypadnie na punkcie podziału. Jak wynika z zasady szufladkowej Dirichleta,
istnieją punkty
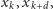 które leżą na tym samym łuku o długości
mniejszej niż
które leżą na tym samym łuku o długości
mniejszej niż
 Wobec tego punkty
Wobec tego punkty
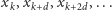 dają
podział całego okręgu i to taki, że dwa dowolne, kolejne punkty są
odległe o mniej niż
dają
podział całego okręgu i to taki, że dwa dowolne, kolejne punkty są
odległe o mniej niż
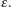 W końcu jedna para punktów musi trafić
w przerwę.
W końcu jedna para punktów musi trafić
w przerwę.
W ten sposób dowiedliśmy, że jakiekolwiek wybierzemy
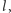 zawsze
musimy następować na jakieś linie.
zawsze
musimy następować na jakieś linie.
Powyższa obserwacja ma wiele ciekawych zastosowań. Zachęcamy Czytelników do udowodnienia na przykład, że dowolny skończony ciąg cyfr może pojawić się jako początek dziesiętnego zapisu pewnej potęgi dwójki.
 przedmiotów w
przedmiotów w
 szufladach – gdy
szufladach – gdy
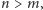 to przynajmniej w jednej z szuflad będą
co najmniej dwa przedmioty.
to przynajmniej w jednej z szuflad będą
co najmniej dwa przedmioty.
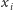 możemy wziąć dowolnie wiele, więc
– po pewnym czasie – zaczniemy umieszczać je w przedziałach, w których
już poprzednio znalazł się jakiś punkt.
możemy wziąć dowolnie wiele, więc
– po pewnym czasie – zaczniemy umieszczać je w przedziałach, w których
już poprzednio znalazł się jakiś punkt.