O potęgach dwójki
Zaczniemy od sformułowania ciekawego problemiku.
Zadanie. Rozpatrzmy ciąg
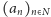 złożony z pierwszych cyfr
kolejnych potęg dwójki:
złożony z pierwszych cyfr
kolejnych potęg dwójki:

Czy w ciągu tym pojawi się kiedykolwiek siódemka?
Zadanie to (i różne jego warianty) można odnaleźć w wielu miejscach, np. w artykule Zbigniewa Marciniaka Spacerujący matematyk ( Delta 7/1991) czy w słynnym podręczniku W.I. Arnolda Równania różniczkowe zwyczajne. Na ogół towarzyszą mu pewne wskazówki czy udowodnione fakty pomocnicze. Autor niniejszego tekstu nie zna jednak miejsca, gdzie wspomniane zadanie można znaleźć w towarzystwie kompletnego rozwiązania, takiego w stylu „kawę na ławę”. Spróbujmy temu zaradzić.
Na początek rozwiązanie rozpaczliwe: za pomocą ołówka i kartki papieru albo nieco nowszych wersji tego narzędzia (dobry kalkulator? komputer?) Wytrwały Czytelnik łatwo sprawdzi, że

Eksperymentując dalej można stwierdzić, na przykład, że siódemka jest
pierwszą cyfrą liczb
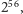
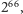
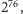
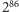 i
i
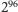 (ale
(ale
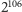 ma za pierwszą cyfrę ósemkę…). Strasznie to jednak niezdarny
sposób.
ma za pierwszą cyfrę ósemkę…). Strasznie to jednak niezdarny
sposób.
Pora na rozwiązanie w miarę eleganckie, pozwalające na wyciągnięcie wielu
wniosków. Na początek trzeba, oczywiście, zrozumieć, co to właściwie
znaczy, że
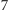 jest pierwszą cyfrą liczby
jest pierwszą cyfrą liczby
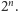 Odpowiedź jest łatwa:
Odpowiedź jest łatwa:
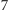 jest pierwszą cyfrą liczby
jest pierwszą cyfrą liczby
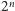 wtedy i tylko wtedy, gdy dla pewnego
wtedy i tylko wtedy, gdy dla pewnego
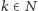 mamy
mamy
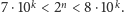 Aby otrzymać prostszy,
równoważny zapis, logarytmujemy te nierówności stronami (przy
podstawie 10); daje to
Aby otrzymać prostszy,
równoważny zapis, logarytmujemy te nierówności stronami (przy
podstawie 10); daje to
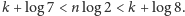 Ponieważ
Ponieważ
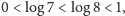 to
to
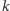 jest częścią całkowitą liczby
jest częścią całkowitą liczby
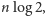 skąd ostatecznie
skąd ostatecznie

Żeby rozwiązać zadanie z początku artykułu, wystarczy teraz skojarzyć ze sobą kilka znanych faktów.
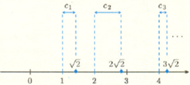
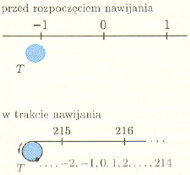
Rys. 1 Wyrazy ciągu
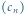 to części ułamkowe kolejnych wielokrotności
to części ułamkowe kolejnych wielokrotności

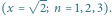
Lemat 2. Jeśli liczba
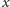 jest niewymierna oraz
jest niewymierna oraz
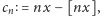 to dla dowolnych
to dla dowolnych
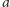 i
i
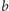 spełniających
spełniających
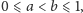 nieskończenie wiele wyrazów
ciągu
nieskończenie wiele wyrazów
ciągu
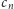 leży w przedziale
leży w przedziale
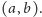
Zanim podamy dowody lematów, popatrzmy na ich konsekwencje. Po pierwsze,
z Lematu 2 zastosowanego dla
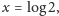
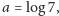
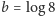 wynika, że siódemka jest pierwszą cyfrą nieskończenie wielu potęg dwójki.
Jeśli zastosujemy Lemat 2 dla
wynika, że siódemka jest pierwszą cyfrą nieskończenie wielu potęg dwójki.
Jeśli zastosujemy Lemat 2 dla
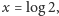
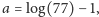
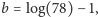 pamiętając, iż
pamiętając, iż
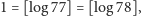 to przekonamy się, że na początku zapisu dziesiętnego liczby
to przekonamy się, że na początku zapisu dziesiętnego liczby
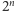 mogą stać również dwie siódemki. Rozumując podobnie nietrudno
stwierdzić, że na początku zapisu dziesiętnego liczby
mogą stać również dwie siódemki. Rozumując podobnie nietrudno
stwierdzić, że na początku zapisu dziesiętnego liczby
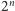 może
wystąpić dowolny skończony ciąg cyfr:
może
wystąpić dowolny skończony ciąg cyfr:
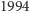 albo
albo
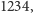 albo
albo
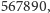 itd... Dla niedowiarków prezentujemy na końcu niniejszego
artykułu kalendarz ważnych dat zestawionych z odpowiednimi potęgami
dwójki.
itd... Dla niedowiarków prezentujemy na końcu niniejszego
artykułu kalendarz ważnych dat zestawionych z odpowiednimi potęgami
dwójki.
Co więcej, prawdziwy jest także
Wniosek. Jeśli liczba naturalna
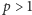 nie jest liczbą postaci
nie jest liczbą postaci
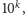
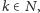 to na początku zapisu dziesiętnego liczby
to na początku zapisu dziesiętnego liczby
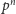 może pojawić się dowolny skończony ciąg cyfr.
może pojawić się dowolny skończony ciąg cyfr.
Dla dowodu wystarczy zauważyć, że liczba
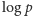 jest niewymierna,
i powtórzyć poprzednie rozważania.
jest niewymierna,
i powtórzyć poprzednie rozważania.
Rys. 2 Weźmy okrąg
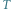 o obwodzie 1. Linie prostą wyobraźmy sobie jako nitkę
(nieskończenie cienką).
o obwodzie 1. Linie prostą wyobraźmy sobie jako nitkę
(nieskończenie cienką).
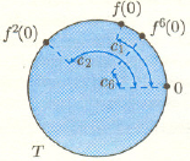
Rys. 3 Długość łuku
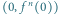 jest równa
jest równa
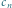 (łuk od punktu
(łuk od punktu
 do
do
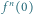 trzeba prowadzić przeciwnie do ruchu wskazówek zegara).
trzeba prowadzić przeciwnie do ruchu wskazówek zegara).
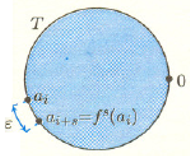
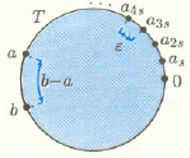
Rys. 4
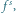 czyli s-ta iteracja
czyli s-ta iteracja
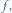 jest obrotem o maleńki kąt
jest obrotem o maleńki kąt
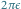 (nie wiemy
tylko, w którą stronę).
(nie wiemy
tylko, w którą stronę).
Dowód Lematu 1. Gdyby dla pewnych
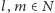 zachodziła równość
zachodziła równość
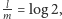 to wprost z definicji logarytmu
mielibyśmy
to wprost z definicji logarytmu
mielibyśmy
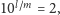 czyli
czyli
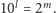 To jest sprzeczność,
bowiem
To jest sprzeczność,
bowiem
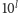 dzieli się przez 5, zaś
dzieli się przez 5, zaś
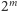 – nie.
– nie.
Dowód Lematu 2. Zauważmy najpierw, że wszystkie wyrazy
ciągu
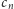 są różne. Gdyby bowiem
są różne. Gdyby bowiem
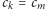 dla
dla
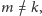 to mielibyśmy
to mielibyśmy
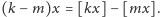 To jest sprzeczność,
bowiem iloczyn różnej od zera liczby całkowitej
To jest sprzeczność,
bowiem iloczyn różnej od zera liczby całkowitej
 oraz liczby
niewymiernej
oraz liczby
niewymiernej
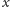 nie może być liczbą całkowitą.
nie może być liczbą całkowitą.
Weźmy teraz takie
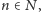 że
że
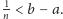 Ponieważ liczby
Ponieważ liczby
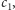
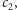 …,
…,
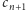 są różne i należą do odcinka
są różne i należą do odcinka
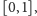 więc z zasady szufladkowej Dirichleta wynika, że dla pewnych
więc z zasady szufladkowej Dirichleta wynika, że dla pewnych
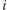 oraz
oraz
 takich, że
takich, że
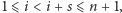 mamy
mamy
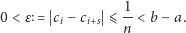 | (1) |
Dalej wygodnie jest posłużyć się następującym wyobrażeniem.
Oś liczbową możemy zwinąć w okrąg
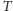 o długości 1
z wyróżnionym punktem 0 (tak, jak pokazuje Rys. 2). Dla
o długości 1
z wyróżnionym punktem 0 (tak, jak pokazuje Rys. 2). Dla
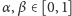 przez
przez
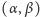 oznaczać będziemy łuk okręgu
oznaczać będziemy łuk okręgu
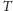 odpowiadający
przedziałowi
odpowiadający
przedziałowi
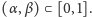
Niech
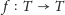 będzie obrotem o kąt
będzie obrotem o kąt
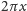 radianów
w kierunku przeciwnym do ruchu wskazówek zegara. Zamiast patrzeć na
liczby
radianów
w kierunku przeciwnym do ruchu wskazówek zegara. Zamiast patrzeć na
liczby
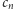 na odcinku
na odcinku
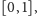 będziemy obserwować na okręgu
będziemy obserwować na okręgu
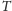 obrazy punktu
obrazy punktu
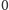 pod działaniem kolejnych iteracji
pod działaniem kolejnych iteracji
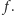 Chwila namysłu pozwala stwierdzić, że długość łuku
Chwila namysłu pozwala stwierdzić, że długość łuku
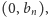 gdzie
gdzie

jest równa
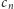 (Rys. 3). Zatem, dzięki nierównościom (1) wiemy,
że długość łuku między punktami
(Rys. 3). Zatem, dzięki nierównościom (1) wiemy,
że długość łuku między punktami
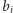 oraz
oraz
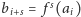 jest
równa
jest
równa
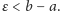 Oznacza to, że
Oznacza to, że
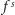 jest obrotem o kąt
jest obrotem o kąt
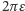 (Rys. 4); kierunek tego obrotu nie ma dla nas znaczenia.
(Rys. 4); kierunek tego obrotu nie ma dla nas znaczenia.
Wynika stąd, oczywiście, że nieskończenie wiele spośród punktów
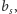
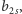
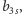 …, należy do łuku
…, należy do łuku
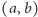 zawartego między
punktami
zawartego między
punktami
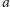 i
i
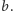 Jeśli bowiem wyjdziemy z ustalonego
punktu
Jeśli bowiem wyjdziemy z ustalonego
punktu
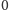 i będziemy chodzić nieskończenie długo po okręgu
i będziemy chodzić nieskończenie długo po okręgu
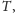 stale w tę samą stronę, stawiając kroczki o długości
stale w tę samą stronę, stawiając kroczki o długości
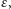 to nieskończenie wiele razy staniemy na łuku
to nieskończenie wiele razy staniemy na łuku
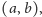 bo jego
długość,
bo jego
długość,
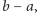 jest większa niż długość naszego kroku,
jest większa niż długość naszego kroku,
 (Rys. 5).
(Rys. 5).
A dlaczego wśród pierwszych wyrazów ciągu utworzonego z pierwszych cyfr kolejnych potęg dwójki nie widać siódemek? Dlaczego ten zdradliwy ciąg wygląda na okresowy? Powód jest prosty: liczba

bardzo dobrze daje się przybliżyć liczbą wymierną 0,3, a dla
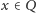 ciąg
ciąg
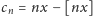 jest okresowy. Dlatego właśnie po obejrzeniu kilkunastu
początkowych wyrazów ciągu
jest okresowy. Dlatego właśnie po obejrzeniu kilkunastu
początkowych wyrazów ciągu
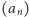 można nabrać niesłusznego
przekonania, że ów ciąg ma okres 10 i siódemka w nim nie występuje,
ósemka zaś pojawia się dość często.
można nabrać niesłusznego
przekonania, że ów ciąg ma okres 10 i siódemka w nim nie występuje,
ósemka zaś pojawia się dość często.
W 1910 roku Wacław Sierpiński, Hermann Weyl oraz P. Bohl udowodnili
niezależnie, że dla niewymiernego
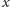 ciąg
ciąg
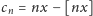 jest
równomiernie rozłożony na odcinku
jest
równomiernie rozłożony na odcinku
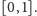 Dokładniej, jeśli weźmiemy
dowolne
Dokładniej, jeśli weźmiemy
dowolne
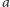 i
i
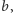
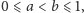 i przez
i przez
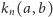 oznaczymy liczbę elementów zbioru
oznaczymy liczbę elementów zbioru
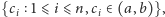 to wówczas
to wówczas
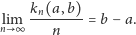 | (2) |
Mówiąc obrazowo i niezbyt precyzyjnie, gdy długo chodzimy po okręgu długości 1 stawiając kroczki niewymiernej długości, to na każdą dziurę będziemy następować mniej więcej z częstością proporcjonalną do długości tej dziury.
Przetłumaczmy ten fakt na język potęg dwójki. Niech
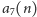 i
i
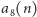 oznaczają odpowiednio liczbę siódemek i ósemek wśród
pierwszych
oznaczają odpowiednio liczbę siódemek i ósemek wśród
pierwszych
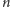 wyrazów ciągu
wyrazów ciągu
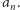 Z równości (2) wynika,
że
Z równości (2) wynika,
że

zatem

Oznacza to, że obserwując odpowiednio długie fragmenty ciągu
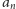 złożonego z pierwszych cyfr kolejnych potęg dwójki zobaczymy nieco więcej
siódemek niż ósemek.
złożonego z pierwszych cyfr kolejnych potęg dwójki zobaczymy nieco więcej
siódemek niż ósemek.
Wspomniany wynik Bohla, Sierpińskiego i Weyla oraz nasz fakcik o siódemkach i ósemkach są w istocie prostymi wnioskami z bardzo ogólnego i głębokiego twierdzenia ergodycznego G.D. Birkhoffa (pochodzącego z 1931 roku), ale to już zupełnie inna historia.
Kalendarz potęg dwójki

Zadanie (dla czytelnika). Dla jakiego
 liczba
liczba
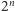 ma na
początku cztery siódemki? A pięć siódemek? Jak oszacować z góry
najmniejszą liczbę
ma na
początku cztery siódemki? A pięć siódemek? Jak oszacować z góry
najmniejszą liczbę
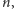 dla której zapis dziesiętny
dla której zapis dziesiętny
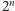 rozpoczyna
się od 1994 kolejnych siódemek?
rozpoczyna
się od 1994 kolejnych siódemek?
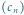 to części ułamkowe kolejnych wielokrotności
to części ułamkowe kolejnych wielokrotności

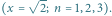
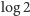
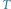 o obwodzie 1. Linie prostą wyobraźmy sobie jako nitkę
(nieskończenie cienką). Nawińmy tą „nitkęńa okrąg
o obwodzie 1. Linie prostą wyobraźmy sobie jako nitkę
(nieskończenie cienką). Nawińmy tą „nitkęńa okrąg
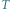 jak na szpulkę. Wówczas
wszystkie punkty prostej odpowiadające liczbom całkowitym śkleją się"do jednego punktu na
okręgu. Punkt ten będziemy oznaczać przez
jak na szpulkę. Wówczas
wszystkie punkty prostej odpowiadające liczbom całkowitym śkleją się"do jednego punktu na
okręgu. Punkt ten będziemy oznaczać przez
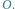
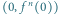 jest równa
jest równa
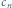 (łuk od punktu
(łuk od punktu
 do
do
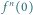 trzeba prowadzić przeciwnie do ruchu wskazówek zegara).
trzeba prowadzić przeciwnie do ruchu wskazówek zegara).
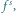 czyli s-ta iteracja
czyli s-ta iteracja
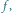 jest obrotem o maleńki kąt
jest obrotem o maleńki kąt
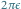 (nie wiemy
tylko, w którą stronę).
(nie wiemy
tylko, w którą stronę).
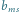 oraz
oraz
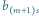 jest równa
jest równa
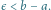 Gdy
Gdy
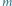 rośnie, to punkty
rośnie, to punkty
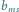 obiegają okrąg dookoła; na
każdym okrążeniu przynajmniej jeden z nich wpada w „dziuręńa łuki
obiegają okrąg dookoła; na
każdym okrążeniu przynajmniej jeden z nich wpada w „dziuręńa łuki
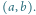
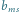 oraz
oraz
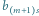 jest równa
jest równa