Ja o liczbach szczęśliwych, ich rozmaitych własnościach oraz pewnych hipotezach dowiedziałem się z artykułu Martina Gardnera w kwartalniku The Mathematical Intelligencer w roku 1997. Okazuje się, że trzynastka też jest szczęśliwa.

Wiadomo, na czym polega metoda sita Eratostenesa, dzięki której znajdujemy liczby pierwsze. No to spróbujmy postąpić podobnie:

Wypisujemy wszystkie liczby naturalne od jedynki, po czym usuwamy co drugą (czyli wszystkie parzyste).

W tym, co zostanie, usuwamy co trzecią, czyli z ciągu 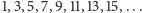wyrzucamy 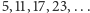i pozostaje:

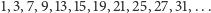
Ale uwaga – usuwaliśmy liczbę co trzecią nie dlatego, że jest po dwójce, ale dlatego, że 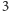była DRUGĄ liczbą w ciągu, na którym dokonywaliśmy operacji! Co teraz? Teraz popatrzmy, jaka liczba jest na TRZECIM miejscu w nowo otrzymanym ciągu. Siódemka. Usuwamy więc co siódmą liczbę; pierwszą wyrzuconą będzie 19. Z nowego ciągu usuwać będziemy liczbę co dziewiątą, bo w nim na CZWARTYM miejscu jest dziewiątka. I tak dalej, w nieskończoność. Liczby, które zostaną, to liczby szczęśliwe. Widzimy, że wśród nich jest trzynastka.

Można odnieść wrażenie, że jest to taka sobie dość dziwna zabawa. Przeczy temu jednak nazwisko pomysłodawcy tej konstrukcji 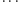O nim za chwilę.

Liczb szczęśliwych jest nieskończenie wiele. Mają pewne ciekawe własności. Choćby taką, że ich „gęstość” w zadanym przedziale jest zaskakująco bliska „gęstości” liczb pierwszych. Na przykład, wśród liczb od 1 do 100 są 23 pierwsze i 25 szczęśliwych. Podobnie jest z „bliźniaczymi liczbami szczęśliwymi” (czyli różniącymi się o 2) i liczbami pierwszymi bliźniaczymi.

Są też otwarte problemy. Na przykład, czy każda liczba parzysta jest sumą dwóch liczb szczęśliwych (niektórym Czytelnikom chyba ten problem coś przypomina)? Sprawdzono komputerowo co najmniej do 100 tysięcy – nie znaleziono wyjątku

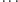
O tym, że liczb szczęśliwych jest nieskończenie wiele, można się przekonać, rozumując podobnie jak w słynnym dowodzie Euklidesa dla liczb pierwszych. Ale na pytanie, czy liczb, które są jednocześnie pierwsze i szczęśliwe, jest nieskończenie wiele, jeszcze niedawno nie znano odpowiedzi i nic nie wiem o tym, by to się zmieniło

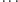
Charles Ashbacher postawił hipotezę, że każda liczba szczęśliwa jest „końcówką” większej liczby szczęśliwej. Na przykład, liczbą 7 kończy się 37, liczbą 13 kończy się 613. To też wciąż jedynie hipoteza.

W artykule Gardnera, o którym mowa na początku, czytamy: The notion of lucky numbers originated about 1955 with Stanislaw Ulam, the great Polish mathematician 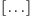 Ulam wyjechał z Polski na stałe w roku 1935, w wieku 26 lat, i do końca życia, do roku 1984, żył i pracował w USA. Zagraniczni autorzy piszą zazwyczaj „American mathematician”, w najlepszym razie „Polish-born American mathematician”. A Gardner napisał „polski matematyk”. To miłe.