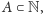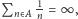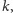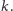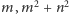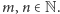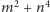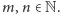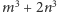Drobiazgi
Dobra dekada dla liczb pierwszych
Oto spektakularne wyniki z lat 1997–2009, dotyczące liczb pierwszych.
Wielomianowy test pierwszości
M. Agrawal, N. Kayal i N. Saxena podali w 2004 roku pierwszy deterministyczny
algorytm weryfikujący, czy dana liczba naturalna
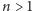 jest pierwsza,
w czasie wielomianowym, tzn. opisanym przez funkcję wielomianową od liczby
cyfr liczby
jest pierwsza,
w czasie wielomianowym, tzn. opisanym przez funkcję wielomianową od liczby
cyfr liczby
 .
.
Twierdzenie 1. Istnieje deterministyczny test pierwszości o złożoności
obliczeniowej
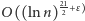 przy dowolnym
przy dowolnym
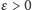 .
.
Długie ciągi arytmetyczne liczb pierwszych
P. Erdős w 1980 roku zaoferował
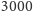 dolarów za rozwiązanie
następującego problemu.
dolarów za rozwiązanie
następującego problemu.
B. Green i T. Tao, używając metod ergodycznych, udowodnili w 2008 roku tę
hipotezę w przypadku, gdy
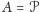 jest zbiorem wszystkich liczb
pierwszych.
jest zbiorem wszystkich liczb
pierwszych.
Twierdzenie 2. Dowolny zbiór
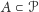 o relatywnie dodatniej górnej
gęstości, tzn. spełniający warunek
o relatywnie dodatniej górnej
gęstości, tzn. spełniający warunek

zawiera nieskończenie wiele ciągów arytmetycznych dowolnej długości.
Pierwsze wartości wielomianów
A. Schinzel w 1958 roku sformułował następujące przypuszczenie.
Hipoteza 2. Niech
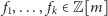 będą wielomianami całkowitymi
i nierozkładalnymi o najwyższych współczynnikach dodatnich. Jeśli dla
każdej liczby pierwszej
będą wielomianami całkowitymi
i nierozkładalnymi o najwyższych współczynnikach dodatnich. Jeśli dla
każdej liczby pierwszej
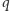 zachodzi
zachodzi
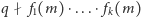 dla
pewnego
dla
pewnego
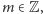 to
to
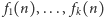 są jednocześnie liczbami
pierwszymi dla nieskończenie wielu
są jednocześnie liczbami
pierwszymi dla nieskończenie wielu
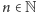 .
.
Hipotezę 2, w przypadku jednego wielomianu liniowego, rozstrzyga twierdzenie Dirichleta o liczbach pierwszych w ciągach arytmetycznych. Udowodnione zostały także, metodami sita, następujące twierdzenia.
Małe odstępy pomiędzy liczbami pierwszymi
D.A. Goldston, J. Pintz i C.Y. Yıldırım udowodnili w 2009 roku, metodami sita Selberga, następujące twierdzenie.