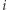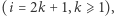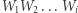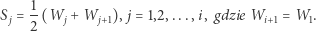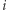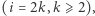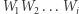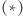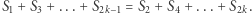Odkryj wielokąt!
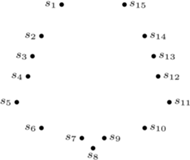
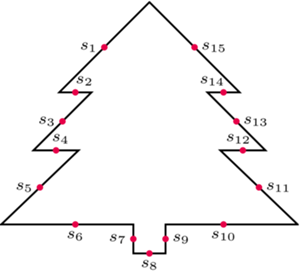
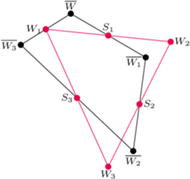
Rys. 1
Punkty z rysunku obok, jako środki kolejnych boków wielokąta, kodują pewien obrazek. Czy potrafisz go odtworzyć? Spróbuj!
Rozpatrzmy sytuację ogólną.
Problem. Czy (jak?, kiedy?) można odtworzyć wielokąt, gdy znamy środki jego kolejnych boków?
Rozpoczniemy od prostego przypadku, gdy na płaszczyźnie dane są trzy różne punkty 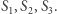 Zbudujemy trójkąt
Zbudujemy trójkąt 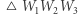 taki, że punkty
taki, że punkty 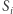 są środkami jego boków. Pokażemy jednocześnie, że złożenie trzech (ogólnie nieparzystej liczby
są środkami jego boków. Pokażemy jednocześnie, że złożenie trzech (ogólnie nieparzystej liczby 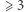 ) symetrii środkowych jest symetrią środkową.
) symetrii środkowych jest symetrią środkową.
Gdy będzie to dla nas wygodne, na punkty płaszczyzny będziemy patrzeć jak na wektory zaczepione w początku układu współrzędnych (oznaczenia wektorów pomijamy).
Rys. 2
Wybieramy na płaszczyźnie punkt 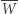 różny od wszystkich punktów
różny od wszystkich punktów 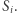 Symetryczne odbicie punktu
Symetryczne odbicie punktu 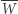 względem punktu
względem punktu 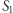 wyznacza punkt
wyznacza punkt 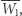 symetryczne odbicie punktu
symetryczne odbicie punktu 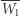 względem
względem 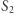 daje punkt
daje punkt 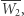 a symetryczne odbicie punktu
a symetryczne odbicie punktu 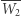 względem
względem 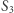 wyznacza punkt
wyznacza punkt 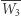 (Rys. 2). Takie przekształcenie płaszczyzny
(Rys. 2). Takie przekształcenie płaszczyzny 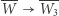 jest symetrią środkową.
jest symetrią środkową.
Istotnie, eliminując 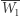 i
i 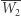 z równań opisujących warunki symetrii
z równań opisujących warunki symetrii
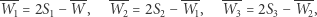 |
otrzymujemy wzór 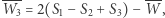 a stąd poszukiwany środek symetrii
a stąd poszukiwany środek symetrii
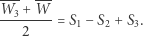 |
Jako jedyny punkt stały przekształcenia 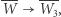 punkt
punkt 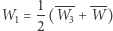 jest jednym z wierzchołków trójkąta
jest jednym z wierzchołków trójkąta 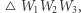 który łatwo wyznaczyć (Rys. 2).
który łatwo wyznaczyć (Rys. 2).

Rozumowanie to działa w przypadku każdej nieparzystej liczby różnych punktów 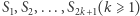 płaszczyzny, które są środkami kolejnych boków wielokąta. Proponujemy samodzielnie przeprowadzić tę konstrukcję dla punktów
płaszczyzny, które są środkami kolejnych boków wielokąta. Proponujemy samodzielnie przeprowadzić tę konstrukcję dla punktów 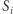 z rysunku 1 - rozwiązanie (o świątecznym charakterze) znajduje się tutaj.
z rysunku 1 - rozwiązanie (o świątecznym charakterze) znajduje się tutaj.
Rozpatrzmy teraz przypadek, gdy na płaszczyźnie dane są cztery różne punkty 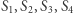 będące środkami kolejnych boków wielokąta. Pokażemy, że w tym przypadku złożenie symetrii środkowych jest translacją.
będące środkami kolejnych boków wielokąta. Pokażemy, że w tym przypadku złożenie symetrii środkowych jest translacją.
Wybieramy na płaszczyźnie punkt 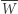 różny od każdego z punktów
różny od każdego z punktów 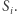 Symetryczne odbicie punktu
Symetryczne odbicie punktu 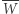 względem punktu
względem punktu 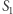 daje punkt
daje punkt 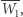 symetryczne odbicie punktu
symetryczne odbicie punktu 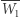 względem
względem 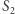 wyznacza punkt
wyznacza punkt 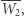 symetryczne odbicie punktu
symetryczne odbicie punktu 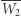 względem
względem 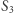 daje
daje 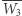 i wreszcie symetryczne odbicie punktu
i wreszcie symetryczne odbicie punktu 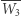 względem
względem 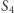 wyznacza punkt
wyznacza punkt 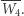 Eliminując punkty
Eliminując punkty 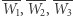 z warunków symetrii
z warunków symetrii
 |
otrzymujemy
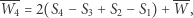 |
co oznacza, że przekształcenie płaszczyzny 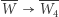 jest translacją o wektor
jest translacją o wektor 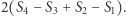 Gdy jest to translacja o wektor niezerowy, nie istnieje czworokąt, którego środki boków są zadanymi wcześniej punktami (gdyż jeden z wierzchołków tego czworokąta musiałby być punktem stałym wspomnianej translacji).
Gdy jest to translacja o wektor niezerowy, nie istnieje czworokąt, którego środki boków są zadanymi wcześniej punktami (gdyż jeden z wierzchołków tego czworokąta musiałby być punktem stałym wspomnianej translacji).
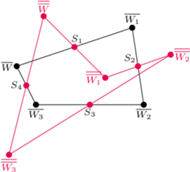
Rys. 3
Równość 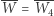 (czyli istnienie czworokąta spełniającego warunki zadania) ma miejsce wtedy i tylko wtedy, gdy
(czyli istnienie czworokąta spełniającego warunki zadania) ma miejsce wtedy i tylko wtedy, gdy
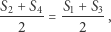 |
czyli gdy środek odcinka łączącego punkty 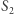 i
i 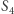 pokrywa się ze środkiem odcinka łączącego punkty
pokrywa się ze środkiem odcinka łączącego punkty 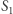 i
i 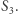 Wówczas czworokątów spełniających warunki zadania jest nieskończenie wiele, punkt
Wówczas czworokątów spełniających warunki zadania jest nieskończenie wiele, punkt 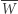 (lub
(lub 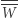 ), różny od każdego punktu
), różny od każdego punktu 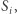 możemy wybrać dowolnie (Rys. 3).
możemy wybrać dowolnie (Rys. 3).
Rozumowanie to pozostaje prawdziwe dla dowolnej parzystej liczby różnych punktów płaszczyzny 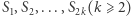 będących środkami kolejnych boków wielokąta. Odkryliśmy w ten sposób następujące twierdzenie:
będących środkami kolejnych boków wielokąta. Odkryliśmy w ten sposób następujące twierdzenie:
Twierdzenie (Edward Kasner, 1903). Niech 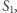
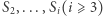 będą różnymi punktami płaszczyzny, które są środkami kolejnych boków wielokąta.
będą różnymi punktami płaszczyzny, które są środkami kolejnych boków wielokąta.
Punkt (b) geometrycznie oznacza, że zbiory punktów 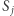 o indeksach nieparzystych oraz parzystych mają ten sam środek ciężkości. Wówczas takich wielokątów jest nieskończenie wiele i dowolny punkt płaszczyzny różny od punktów
o indeksach nieparzystych oraz parzystych mają ten sam środek ciężkości. Wówczas takich wielokątów jest nieskończenie wiele i dowolny punkt płaszczyzny różny od punktów 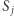 może pełnić rolę wierzchołka
może pełnić rolę wierzchołka 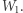
Powyższe uwagi nie wyczerpują zagadnienia. Rozważania można prowadzić, rozpatrując dla 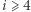 "wieloboki przestrzenne".
"wieloboki przestrzenne".
Opisana sytuacja to prosta ilustracja działania skończonych szeregów Fouriera, ogólniej - analizy harmonicznej, która z małego zbioru informacji stara się odtworzyć ogólniejsze zjawisko. Czasem można to zrobić bardzo precyzyjnie, innym razem tylko w ogólnym zarysie, a czasem jest to niemożliwe.