Czworokąty bliźniacze
Przypuśćmy, że dane mamy dwa czworokąty wypukłe 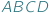 i
i  takie, że każdemu bokowi jednego odpowiada pewien równoległy doń bok drugiego, a każdej przekątnej - równoległa przekątna. Na pierwszy rzut oka wydawać by się mogło, że takie czworokąty muszą być podobne, jest jednak druga możliwość - wówczas czworokąty te są bliźniacze...
takie, że każdemu bokowi jednego odpowiada pewien równoległy doń bok drugiego, a każdej przekątnej - równoległa przekątna. Na pierwszy rzut oka wydawać by się mogło, że takie czworokąty muszą być podobne, jest jednak druga możliwość - wówczas czworokąty te są bliźniacze...

Rys. 1.
Dokładna definicja tego określenia jest następująca: czworokąty wypukłe 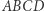 i
i 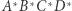 nazwiemy bliźniaczymi, jeśli spełnione są dwa warunki:
nazwiemy bliźniaczymi, jeśli spełnione są dwa warunki:
 |
oraz
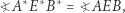 |
gdzie punkty 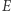 i
i 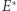 są odpowiednio przecięciami prostych
są odpowiednio przecięciami prostych  i
i 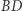 oraz
oraz 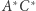 i
i 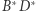 (Rys. 1). Wówczas będziemy pisać
(Rys. 1). Wówczas będziemy pisać 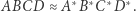 Taka definicja par czworokątów bliźniaczych jest "porządna", to znaczy: dla każdego czworokąta wypukłego
Taka definicja par czworokątów bliźniaczych jest "porządna", to znaczy: dla każdego czworokąta wypukłego  istnieje dokładnie jeden, z dokładnością do podobieństwa, czworokąt do niego bliźniaczy
istnieje dokładnie jeden, z dokładnością do podobieństwa, czworokąt do niego bliźniaczy 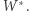 Dodatkowo czworokąt bliźniaczy do czworokąta
Dodatkowo czworokąt bliźniaczy do czworokąta  to po prostu czworokąt
to po prostu czworokąt 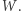
Spójrzmy na dwie konstrukcje czworokąta bliźniaczego dla danego czworokąta 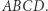

Rys. 2.

Rys. 3.
Konstrukcja 1. Niech  będzie punktem przecięcia prostej
będzie punktem przecięcia prostej 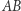 i prostej równoległej do prostej
i prostej równoległej do prostej 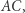 przechodzącej przez punkt
przechodzącej przez punkt  zaś
zaś  niech będzie punktem przecięcia prostej
niech będzie punktem przecięcia prostej 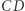 i prostej równoległej do prostej
i prostej równoległej do prostej 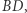 przechodzącej przez punkt
przechodzącej przez punkt  (Rys. 2). Wówczas
(Rys. 2). Wówczas 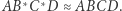
Konstrukcja 2. Rozważmy inwersję o środku w punkcie przecięcia przekątnych 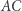 i
i 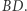 Niech obrazami punktów
Niech obrazami punktów 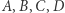 w tej inwersji będą odpowiednio punkty
w tej inwersji będą odpowiednio punkty 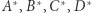 (Rys. 3). Wówczas
(Rys. 3). Wówczas 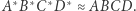
Sprawdzenie, wprost z definicji, że powyższe pary czworokątów są istotnie bliźniacze, pozostawiamy Czytelnikowi.
W geometrii rozważane są przeróżne układy współrzędnych. Układ współrzędnych kartezjańskich, przypisanie punktom płaszczyzny liczb zespolonych, ale też układy odniesienia względem trójkąta: współrzędne barycentryczne czy trzyliniowe (wyrażające stosunki odległości punktu od boków ustalonego trójkąta). My będziemy rozważać jeszcze inny układ współrzędnych, w odniesieniu do czworokąta. Niech dany będzie czworokąt  oraz punkt
oraz punkt 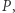 wtedy współrzędnymi kątowymi punktu
wtedy współrzędnymi kątowymi punktu  względem czworokąta
względem czworokąta 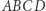 nazwiemy czwórkę:
nazwiemy czwórkę:
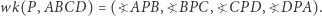 |
Okazuje się, że tak zdefiniowane współrzędne kątowe mają wiele wspólnego z czworokątami bliźniaczymi. Dokładniej mówi o tym następujące twierdzenie.

Rys. 4.
Dowód. Rozważmy antyinwersję  gdzie
gdzie 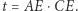 Łatwo zauważyć, że
Łatwo zauważyć, że 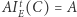 oraz
oraz 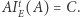 Oznaczmy
Oznaczmy 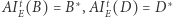 oraz
oraz  (Rys. 4). Na mocy prawdziwości Konstrukcji 2 czworokąty
(Rys. 4). Na mocy prawdziwości Konstrukcji 2 czworokąty 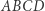 i
i 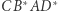 są bliźniacze. Niech
są bliźniacze. Niech  i
i 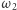 będą odpowiednio okręgami opisanymi na trójkątach
będą odpowiednio okręgami opisanymi na trójkątach 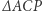 i
i 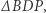 niech punkt
niech punkt 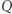 będzie drugim przecięciem okręgów
będzie drugim przecięciem okręgów  i
i 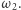 Wykażę, że szukanym punktem
Wykażę, że szukanym punktem 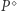 jest punkt
jest punkt 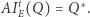
Wystarczy uzasadnić, że
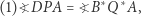 |
(1) |
gdyż pozostałe do sprawdzenia równości są analogiczne. Ponieważ 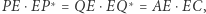 więc punkty
więc punkty 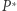 i
i 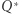 leżą na okręgu
leżą na okręgu 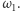
Na mocy Własności 1 (patrz przypis) wystarczy zatem wykazać, że proste 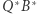 i
i 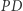 przecinają się na okręgu
przecinają się na okręgu 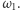 To zaś, ponownie na mocy Własności 1, jest równoważne równości
To zaś, ponownie na mocy Własności 1, jest równoważne równości
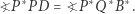 |
(2) |
Niech 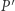 będzie drugim przecięciem prostej
będzie drugim przecięciem prostej 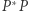 z okręgiem
z okręgiem 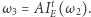 Ponieważ okrąg
Ponieważ okrąg 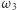 przechodzi na okrąg
przechodzi na okrąg  w pewnej jednokładności o środku w
w pewnej jednokładności o środku w 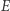 (co wynika z definicji inwersji), więc proste
(co wynika z definicji inwersji), więc proste 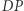 i
i 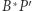 są równoległe, stąd
są równoległe, stąd
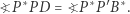 |
(3) |
Ponieważ punkty 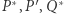 i
i 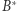 leżą na jednym okręgu, to na mocy Własności 1 zachodzi
leżą na jednym okręgu, to na mocy Własności 1 zachodzi
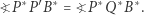 |
(4) |
Równości (3) i (4) implikują (2), więc również (1), co kończy dowód.
W dowodzeniu kolejnych twierdzeń przyda nam się następujące stwierdzenie, które jest w pewnym sensie odwróceniem Twierdzenia 1. Jego dowód pozostawiamy Czytelnikowi.
Stwierdzenie. Jeśli kąty w odpowiadających wierzchołkach czworokątów 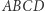 i
i 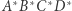 sumują się do 180 stopni oraz istnieją takie punkty
sumują się do 180 stopni oraz istnieją takie punkty 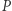 i
i 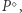 że
że  to czworokąty te są bliźniacze.
to czworokąty te są bliźniacze.
Wyposażeni w przedstawione narzędzia możemy udowodnić poniższe Twierdzenia 2 i 3. Czytelnika Dociekliwego zachęcamy do samodzielnego zmierzenia się z tymi twierdzeniami przed przeczytaniem zamieszczonych dowodów. Można spróbować uzasadnić je bez powoływania się na Twierdzenie 1 (takie dowody są przedstawione w pełnej wersji mojej pracy Czworokąty bliźniacze.
Dowód. Na półprostych 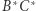 i
i 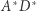 wybierzmy punkty
wybierzmy punkty 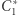 i
i 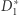 tak, że odcinki
tak, że odcinki 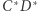 i
i 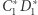 są równoległe oraz w czworokąt
są równoległe oraz w czworokąt 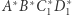 można wpisać okrąg. Wystarczy udowodnić, że
można wpisać okrąg. Wystarczy udowodnić, że 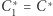 i
i 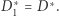
Niech 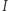 i
i 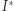 będą środkami okręgów wpisanych w
będą środkami okręgów wpisanych w 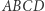 i
i 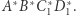 Zauważmy, że
Zauważmy, że
 |
oraz
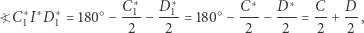 |
zatem ponieważ 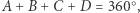 to
to 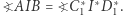 W tej sytuacji punkty
W tej sytuacji punkty  i
i 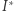 mają takie same pierwsze współrzędne kątowe odpowiednio względem czworokątów
mają takie same pierwsze współrzędne kątowe odpowiednio względem czworokątów 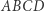 i
i 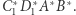 Analogicznie możemy dowieść, że pozostałe trzy współrzędne też są takie same, zatem
Analogicznie możemy dowieść, że pozostałe trzy współrzędne też są takie same, zatem 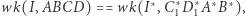 skąd na mocy Stwierdzenia wnioskujemy, że
skąd na mocy Stwierdzenia wnioskujemy, że 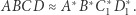 Zgodnie z założeniami mamy
Zgodnie z założeniami mamy 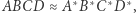 zatem czworokąty
zatem czworokąty 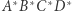 i
i 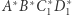 są podobne, skąd łatwo wywnioskować, że
są podobne, skąd łatwo wywnioskować, że 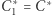 i
i 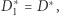 a to kończy dowód.
a to kończy dowód.
Dowód. Niech punkt 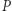 będzie przecięciem wyżej wymienionych trzech prostych. Załóżmy ponadto, że
będzie przecięciem wyżej wymienionych trzech prostych. Załóżmy ponadto, że 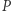 nie leży na okręgu opisanym na trójkącie
nie leży na okręgu opisanym na trójkącie  (dowód w przeciwnym przypadku jest raczej techniczny i mniej ciekawy).
(dowód w przeciwnym przypadku jest raczej techniczny i mniej ciekawy).
Rozważmy taki punkt  by
by
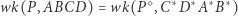 |
(5) |
(istnienie takiego punktu gwarantuje nam Twierdzenie 1). Ponieważ proste 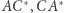 i
i 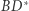 są współpękowe, to zachodzą równości kątów
są współpękowe, to zachodzą równości kątów
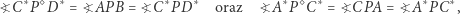 |
one zaś implikują, że czworokąty 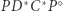 i
i  są wpisane w okręgi. Ponieważ czworokąt
są wpisane w okręgi. Ponieważ czworokąt  nie jest wpisany w okrąg, więc
nie jest wpisany w okrąg, więc  lub
lub  W analogiczny sposób możemy jednak udowodnić, że
W analogiczny sposób możemy jednak udowodnić, że 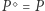 lub
lub 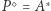 (role punktów
(role punktów 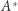 i
i  są symetryczne), zatem musi być
są symetryczne), zatem musi być 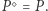 Z (5) wynika zatem, że
Z (5) wynika zatem, że 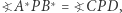 z tego zaś mamy, że punkty
z tego zaś mamy, że punkty  i
i 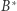 są współliniowe, więc teza zachodzi.
są współliniowe, więc teza zachodzi.
Na zakończenie pozostawiamy dla Czytelnika dwa zadania, które da się rozwiązać, wykorzystując czworokąty bliźniacze - rozwiązania te można znaleźć w pełnej wersji mojej pracy zgłoszonej na Konkurs Uczniowskich Prac z Matematyki im. Pawła Domańskiego. Pierwsze z nich zostało przedstawione na stronie www.gogeometry.com jako problem 1351, bez znanego geometrycznego dowodu; to właśnie ono było dla mnie motywacją do napisania pracy. Drugie zadanie jest zadaniem autorskim, powstałym w trakcie badania czworokątów bliźniaczych.
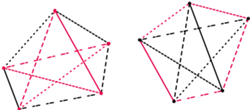
Uwaga końcowa. Jak już nadmieniłem we wstępie, czworokąty bliźniacze na płaszczyźnie da się narysować w taki sposób, by ich odpowiadające boki i przekątne były równoległe. Można się zastanowić, czy istnieją inne pary 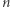 -kątów o tej własności, że da się je narysować w taki sposób, by ich odpowiadające sobie boki i przekątne były do siebie równoległe oraz by
-kątów o tej własności, że da się je narysować w taki sposób, by ich odpowiadające sobie boki i przekątne były do siebie równoległe oraz by  -kąty te nie były do siebie podobne. Dla
-kąty te nie były do siebie podobne. Dla 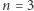 oczywiście taka para nie istnieje, z kolei przykład dla
oczywiście taka para nie istnieje, z kolei przykład dla  przedstawiony jest na marginesie. Potrafię udowodnić, że takich par jest stosunkowo mało, w szczególności nie dla każdego
przedstawiony jest na marginesie. Potrafię udowodnić, że takich par jest stosunkowo mało, w szczególności nie dla każdego 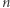 -kąta istnieje tak zdefiniowany
-kąta istnieje tak zdefiniowany  -kąt bliźniaczy. Zachęcam Czytelnika do próby znalezienia odpowiedzi na to pytanie!
-kąt bliźniaczy. Zachęcam Czytelnika do próby znalezienia odpowiedzi na to pytanie!
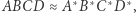
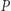
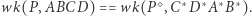
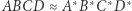



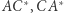
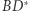
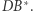
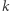 i
i  nazywamy taką liczbę
nazywamy taką liczbę 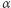 z przedziału
z przedziału  że po obróceniu prostej
że po obróceniu prostej  przeciwnie do ruchu wskazówek zegara o kąt
przeciwnie do ruchu wskazówek zegara o kąt 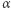 proste
proste 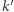 i
i 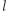 będą równoległe. Dla kątów skierowanych zachodzi następująca własność: kąt skierowany między prostą
będą równoległe. Dla kątów skierowanych zachodzi następująca własność: kąt skierowany między prostą 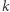 i
i 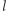 jest równy kątowi skierowanemu między prostą
jest równy kątowi skierowanemu między prostą 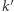 i
i 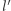 i różny od
i różny od 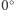 wtedy i tylko wtedy, gdy punkty
wtedy i tylko wtedy, gdy punkty 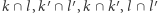 leżą na jednym okręgu. Będę ją nazywał Własnością 1.
leżą na jednym okręgu. Będę ją nazywał Własnością 1.