Drogi Czytelniku, narysuj takie cztery okręgi, że I przecina się z II, II z III, III z IV i IV z I. Powstanie osiem punktów - wspólne punkty I i II nazwij 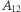i 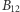i podobnie pozostałe. Jeśli trafi Ci się tak, że - jak na rysunku - punkty 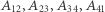leżą na jednym okręgu, to wówczas punkty 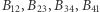też będą leżały na jednym okręgu (jak tutaj) lub na jednej prostej. Udowodnij to!

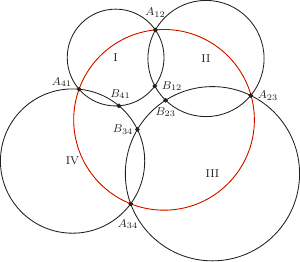
Podobnie gdyby punkty 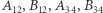leżały na jednej prostej lub jednym okręgu, to wówczas pozostałe punkty też leżałyby na jednej prostej lub na jednym okręgu.

A czy te prawidłowości będą miały miejsce, gdy niektóre punkty 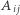zamienisz z punktami