Drobiazgi

Rektyfikacja i kwadratura według Archimedesa

Archimedes rektyfikację okręgu i kwadraturę koła wykonał za pomocą swojej spirali, czyli krzywej opisanej w układzie biegunowym przez 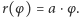$r(φ ) = a ⋅φ.$ Jeśli odcinek 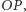$OP$ łączący punkt spirali odpowiadający 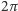$2π$ z jej początkiem, będzie miał długość 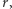$|r,$ to styczna do spirali w tym punkcie przetnie wychodzącą z 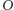$O$ półprostą prostopadłą do 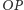$OP |$ w takim punkcie 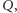$Q, |$ że $| OQ$

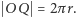
Czytelniku, sprawdź!

Mamy więc zarówno rektyfikację okręgu (to ten poziomy odcinek), jak i kwadraturę koła, bo pole powstałego trójkąta to 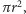$2 πr ,$ a trójkąt na kwadrat zamienić łatwo - choćby nożyczkami.