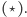Drobiazgi
Zagadnienie Fermata w jednej linijce!
Tzw. zagadnienie Fermata to pytanie o to, gdzie wewnątrz danego trójkąta  należy umieścić punkt
należy umieścić punkt 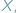 aby suma długości odcinków
aby suma długości odcinków 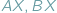 i
i 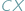 przyjęła najmniejszą wartość.
przyjęła najmniejszą wartość.
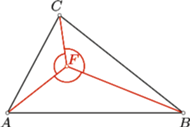
Rys. 1
Okazuje się, że jeśli każdy z kątów wewnętrznych trójkąta 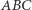 jest mniejszy od
jest mniejszy od 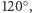 to punkt
to punkt 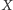 należy wybrać w miejscu, z którego widać wszystkie jego boki pod tym samym kątem. Innymi słowy, punkt
należy wybrać w miejscu, z którego widać wszystkie jego boki pod tym samym kątem. Innymi słowy, punkt 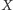 powinien się znaleźć w punkcie
powinien się znaleźć w punkcie 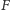 spełniającym warunek
spełniającym warunek
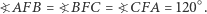 |
Uzasadnienie, że taki punkt 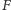 (Rys. 1) istnieje pozostawię Czytelnikowi jako ćwiczenie. Natomiast dowód, że dla każdego punktu
(Rys. 1) istnieje pozostawię Czytelnikowi jako ćwiczenie. Natomiast dowód, że dla każdego punktu 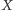 spełniona jest nierówność
spełniona jest nierówność
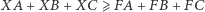 |
przeprowadzę w jednej linijce:
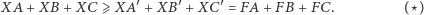 |
A teraz kilka linijek, tłumaczących linijkę powyższą.:)
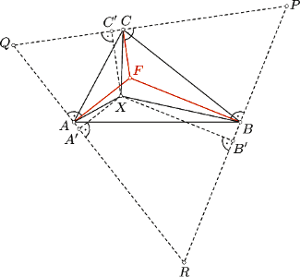
Rys. 2
Proste prostopadłe do odcinków 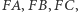 przechodzące odpowiednio przez punkty
przechodzące odpowiednio przez punkty 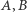 i
i 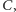 wyznaczają trójkąt równoboczny - oznaczmy go przez
wyznaczają trójkąt równoboczny - oznaczmy go przez 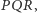 jak na rysunku 2.
jak na rysunku 2.
Jeśli przez 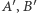 i
i 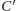 oznaczymy rzuty prostokątne punktu
oznaczymy rzuty prostokątne punktu 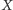 na odpowiednie boki trójkąta
na odpowiednie boki trójkąta 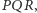 to oczywiście
to oczywiście 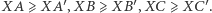 Po dodaniu stronami uzyskujemy nierówność znajdującą się w linijce
Po dodaniu stronami uzyskujemy nierówność znajdującą się w linijce 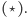
Wiadomo z kolei, że dla dowolnego punktu leżącego wewnątrz trójkąta równobocznego suma odległości tego punktu od boków trójkąta jest stała, niezależna od wyboru punktu (równa wysokości trójkąta). Stąd natychmiast wynika równość z linijki