Wpisywanie
W geometrii dyskretnej przyjęło się mówić, że wielokąt jest wpisany w inny wielokąt, gdy ma wierzchołki na prostych zawierających boki tego drugiego wielokąta. Od czasu Hilberta tego zwrotu używa się i w przypadku "zwyczajnej" geometrii.
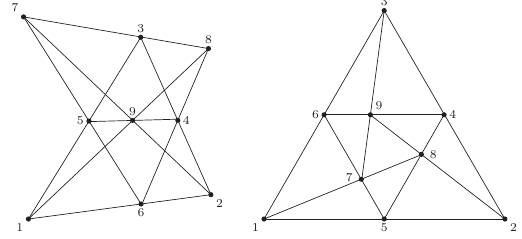
Na obu rysunkach trójkąt 123 jest wpisany w trójkąt 789, ten z kolei jest wpisany w trójkąt 456, ten zaś w trójkąt 123.
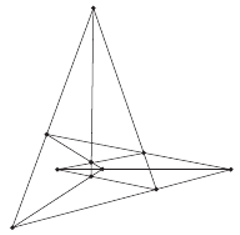
Jak widać, można to zrobić nawet na co najmniej dwa sposoby. Polecam Czytelnikowi sprawdzenie, że ten łańcuszek nie może być krótszy, czyli że nie ma takich trójkątów 
i 
by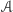 
był wpisany w 
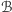i równocześnie 
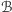był wpisany w 
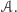To nietrudne.
A jak jest dla czworokątów? Bo dla pięciokątów jest to możliwe. Wybierając odpowiednio odcinki z rysunku na marginesie, można wskazać dwa pięciokąty, z których każdy jest wpisany w pozostały.
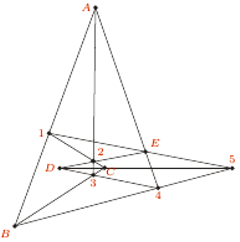
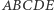i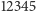 
są wzajemnie wpisane.