Czarodziej wyciągnął zza pazuchy kartkę, na której były narysowane dwa odcinki i rzucił:

- Krótszy z narysowanych odcinków ma długość 1, dłuższy 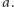Żądam odcinka długości !

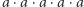Król pochylił się nad kartką, zmarszczył czoło i po chwili odparł z wielką ulgą:

- Przecież to proste! Wystarczy wziąć linijkę, zmierzyć dłuższy odcinek, obliczyć wartość 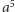i odmierzyć odcinek o obliczonej długości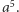

- Oczywiście w zadaniu jest pewien kruczek... - kruczki były dobrą czarodziejską praktyką. - Zaczarowałem wszystkie linijki w królestwie tak, że zniknęły z nich podziałki. Do dyspozycji masz jedynie odcinki długości 1 i 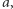których nie sposób dokładnie zmierzyć, linijkę bez podziałki oraz cyrkiel. - uśmiechnął się przebiegle.

Król czym prędzej wyciągnął swoją królewską linijkę i, o zgrozo, stwierdził, że podziałka faktycznie zniknęła. Sposępniał… W głowie pobrzmiewały mu przeklęte słowa pewnego mędrca, że w matematyce nie ma specjalnej drogi dla królów.

- Królu, masz czas do jutra, do godziny będącej najmniejszą liczbą naturalną, mającą dokładnie sześć różnych dzielników! Jeśli do tego czasu nie otrzymam rozwiązania, królewna zostanie zamknięta w mojej wieży na zawsze! - rzekł czarnoksiężnik głosem tak donośnym, że echo rozniosło po królestwie wieść o zadaniu w tempie wykładniczym.

Wielu mieszkańców królestwa próbowało je rozwiązać, ale suma wyników ich starań niezmiennie była zbiorem pustym. A czas uciekał… Dopiero nad ranem następnego dnia zadanie dotarło do pewnego rycerza, będącego z zamiłowania geometrą. Rozważał właśnie sprawę zakupu kanapy. Chciał, żeby była możliwie jak największa, ale na tyle mała, żeby można było ją przesunąć korytarzem w kształcie litery L i szerokości 1 metra. Problem okazał się trudniejszy, niż rycerzowi się zdawało (problem przesunięcia sofy) i stwierdził, że dobrze byłoby na chwilę oderwać się od bieżącego zajęcia. Zastanowił się chwilę nad sprawą odcinków czarnoksiężnika, zakręcił swoim wąsem, zastanowił się kolejną chwilę i czym prędzej pognał do królewskiego pałacu zaprezentować rozwiązanie. Dotarł tuż przed dwunastą i rzekł ciepłym głosem do zapłakanej królewny:

- Wiem, jak rozwiązać zadanie czarodzieja.

Król, zaskoczony pewnością siebie rycerza, zarządził. - Dajcie mu papier. Niezwłocznie podano mu kartkę oraz uzbrojenie w postaci ołówka, cyrkla i nawet królewskiej linijki.

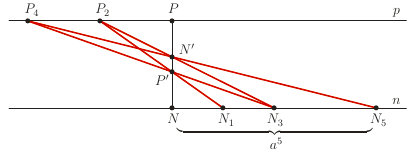
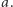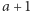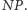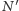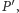- Mamy odcinki długości 1 i Skonstruowanie odcinka długości to nie problem, oznaczmy go Następnie na tym odcinku zaznaczamy takie punkty oraz że 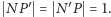Z pomocą cyrkla to zupełna błahostka.

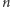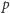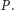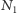- Teraz prowadzimy proste i prostopadłe do odcinka i zawierające, odpowiednio, punkty i - tutaj rycerz namachał się nieco cyrklem. - Na prostej zaznaczamy punkt tak, że 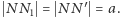Jesteśmy już tak blisko!

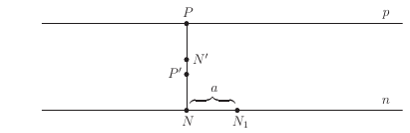
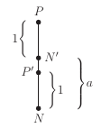
- Przez punkty 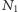i 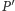prowadzimy prostą. Punkt jej przecięcia z prostą 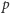oznaczmy 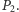Długość odcinka 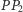jest równa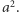

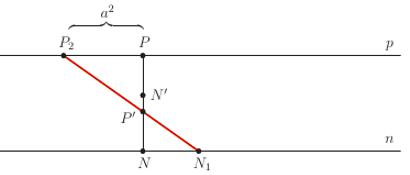
- Z punktu 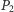prowadzimy prostą, przechodzącą przez punkt 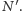Punkt jej przecięcia z prostą oznaczmy przez 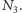Długość odcinka 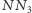to 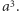Jeszcze raz, podobnie, przechodzimy przez punkt 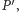otrzymując punkt 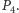Potem przechodzimy przez punkt 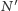i otrzymujemy punkt 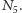Odcinek 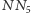jest rozwiązaniem Twojego zadania, czarnoksiężniku.

Czarnoksiężnik już przy punkcie 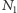zrozumiał swoja sromotną klęskę. Dobrze wiedział, że odcinek 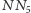ma długość 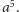Rycerz widząc pokonaną minę czarodzieja, rzekł zuchwale:

- W mig mogę skonstruować odcinek długości 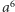czy 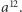Nawet więcej, delikatnie modyfikując metodę, mogę otrzymać odcinki o długości 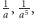czy 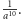Królewna w lot pojęła, na czym polegała metoda rycerza i sama, tak dla rozrywki, zaczęła konstruować odpowiednie odcinki.

- Ciekawe… Rycerzu, w Twojej metodzie łamana powstająca z odcinków miedzy prostymi równoległymi przypomina gwiazdę. Nazwijmy ją gwiazdą potęgową!

Dobre wychowanie czarnoksiężnika kazało mu pogratulować rycerzowi, odczarować wszystkie linijki w królestwie i zniknąć do czasu, kiedy wszyscy o nim zapomną. Królewna, zobaczywszy, jak biegły w geometrii jest jej wybawca, zgodziła się zostać jego żoną. Rycerz został królewiczem i długo i szczęśliwie zabawiał księżniczkę geometrią, pokazał między innnymi, w jaki sposób mając dane dwa odcinki i 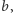konstruować odcinek, którego długość jest iloczynem 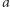i 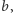opowiedział o problemie sofy. Oczywiście, żyli też długo i szczęśliwie i codziennie wieczorem w blasku zamkowego kominka wspólnie radośnie uprawiali matematykę.