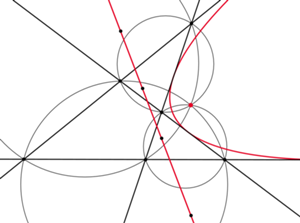
Ale gdy narysujemy ortocentra tych trójkątów (czyli punkty przecięcia wysokości każdego z nich - to te czarne kropki na rysunku), to okaże się, że punkty te leżą na jednej prostej - kto umie to udowodnić?

A gdy z kolei narysujemy okręgi opisane na tych trójkątach, okaże się, że wszystkie one mają punkt wspólny - czy to ma związek z poprzednim spostrzeżeniem? No i jak to udowodnić?

To teraz coś jeszcze. Gdy narysujemy kilka (lepiej kilkanaście) punktów jednakowo odległych od prostej łączącej ortocentra i od wspólnego punktu okręgów, to może nam przyjść do głowy, że punkty te leżą na paraboli, dla której kolorowa prosta jest kierownicą, a kolorowy punkt ogniskiem.

To wygląda już na kompletne szaleństwo, ale jest prawdą. Co więcej, parabola ta jest styczna do każdej z wyjściowych czterech prostych.

Cóż - trzeba przemyśleć, jak by i to udowodnić. Taka rozrywka na jesienne dżdżyste wieczory.