Mała Delta

Kąty i Okrąg

Każdy zna twierdzenie o kącie zewnętrznym trójkąta: jest on równy sumie kątów wewnętrznych do niego nie przyległych (Rys. 1), co bierze się z faktu, że suma kątów przyległych jest równa sumie kątów trójkąta. Z twierdzenia tego wynika nietrudno twierdzenie o kącie wpisanym i środkowym: kąt wpisany jest równy 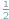$1 2$ kąta środkowego opartego na tym samym łuku.

Wynika to z faktu, że w sytuacji z rysunku 2 mamy 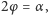$|2φ =α ,$ każda zaś para kątów, o jakich mówi twierdzenie, daje się przedstawić jako suma (Rys. 3) bądź jako różnica (Rys. 4) sytuacji z rysunku 2

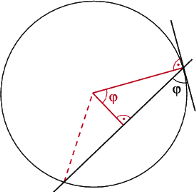
Mniej popularne jest pojęcie kąta dopisanego, czyli kąta między cięciwą okręgu i styczną do tego okręgu w jednym z końców tej cięciwy (Rys. 5). Stwierdzamy bez trudu, że kąt dopisany jest równy 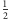$|12$ kąta środkowego opartego na tym samym łuku, albowiem (Rys. 6) wynika to z równości kątów o ramionach odpowiednio prostopadłych. Zatem kąt wpisany oparty na danym łuku (jest ich wiele) jest równy kątowi dopisanemu opartemu na tym samym łuku (są takie dwa, Rys. 7).

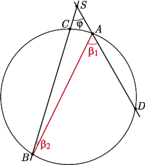
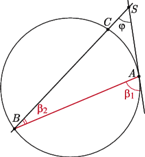
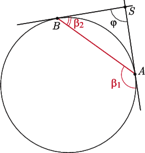
A co się dzieje, gdy mamy do czynienia z okręgiem i kątem, który nie jest ani środkowy, ani wpisany, ani dopisany?

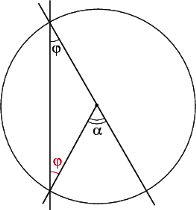
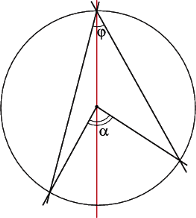
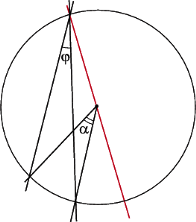
Oczywiście, interesować nas będą tylko sytuacje, gdy proste zawierające ramiona kąta będą siecznymi bądź stycznymi do okręgu. Sytuacjie takie są cztery, co przedstawiają rysunki 8-11.

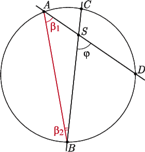
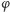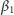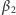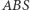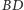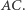I niewiele trzeba do nich dorysować, by zauważyć, że w pierwszym przypadku rozpatrywany kąt $|φ$ (Rys. 12) jest równy sumie kątów wpisanych $|β1$ i $|β2$ (jako kąt zewnętrzny trójkąta $|ABS$ ), a więc równy połowie sumy kątów środkowych opartych odpowiednio na łukach $|BD$ i $AC.$ W pozostałych trzech przypadkach za każdym razem otrzymujemy 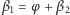$1 β = φ+ β2$ (znów jako kąt zewnętrzny trójkąta 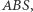$ABS,$ Rys. 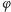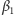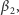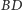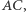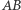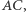13-15), a więc rozpatrywany kąt $φ$ jest równy różnicy kątów wpisanych, względnie dopisanych, $β 1$ i $β 2,$ a tym samym równy połowie różnicy kątów środkowych opartych odpowiednio w drugim przypadku na łukach $BD$ i $|AC,$ w trzecim na łukach $AB |$ i $AC, |$ w ostatnim wreszcie na obu łukach 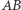$AB$ zawartych we wnętrzu rozpatrywanego kąta.

Możemy teraz uwolnić się od oznaczeń i sformułować ogólne twierdzenie dotyczące kątów i okręgu.

Twierdzenie. Kąt, którego ramiona zawarte są w siecznych lub stycznych do okręgu, jest - w przypadku, gdy wierzchołek kąta leży wewnątrz tego okręgu (lub na nim) - równy połowie sumy kątów środkowych opartych na łukach, które wycinają z tego okręgu proste zawierające ramiona kąta, lub - w przypadku, gdy wierzchołek kąta leży na zewnątrz tego okręgu - połowie ich różnicy.

Twierdzenie to zawiera jako szczególne przypadki zarówno "szkolne" twierdzenie o kącie wpisanym, jak i mniej znane twierdzenie o kącie dopisanym. A dowód ma - jak było widać - łatwy. Nic więc nie tłumaczy jego nieobecności w szkole (chyba że nie znają go piszący podręczniki, ale to przecież tak mało prawdopodobne).