Styczna do okręgu

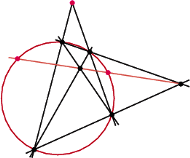
Dany jest okrąg i punkt na zewnątrz.

Przez ten punkt prowadzimy dwie sieczne różnej długości.

Punkty przecięcia tych siecznych z okręgiem łączymy prostymi w pary na pozostałe dwa sposoby.

Przez nowo powstałe punkty przecięcia prowadzimy prostą

Jeśli punkty otrzymane z jej przecięcia z okręgiem połączymy z początkowym punktem, to uzyskamy styczne do okręgu.

---

Brakujący punkt

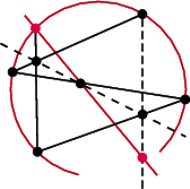
Dany jest okrąg, ale nie cały, i prosta przecinająca go, ale przechodząca też przez dziurę.

Drugi punkt przecięcia okręgu z daną prostą znajdujemy, dobierając na okręgu jeszcze cztery punkty i łącząc je łamaną (dla ułatwienia ponumerujmy kolejno jej odcinki).

Punkt przecięcia prostych zawierających odcinki 1 i 4 łączymy z punktem przecięcia danej prostej z prostą zawierającą odcinek 3 i przez punkt przecięcia tej prostej z prostą zawierającą odcinek 2 prowadzimy prostą z ostatniego wierzchołka łamanej.

Przecina ona daną prostą w punkcie leżącym na danym okręgu.

***

Obie te konstrukcje korzystają z twierdzeń geometrii rzutowej, której nie omawia się w szkole. Ale przecież nikt nam nie każe posługiwać się w życiu tylko tym, co poznaliśmy na lekcjach. Obie powyższe konstrukcje bez zmian stosują się też do elips i hiperbol.