Kolorowanie płaszczyzny, prostych i okręgów
O kolorowaniu płaszczyzny raz jeszcze...
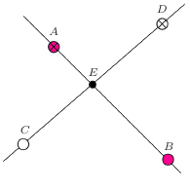
Rys. 1
Na drugim etapie VIII Olimpiady Matematycznej Gimnazjalistów (obecnie Olimpiady Matematycznej Juniorów) pojawiło się następujące zadanie:
Zadanie. Każdy punkt płaszczyzny należy pomalować na pewien kolor w taki sposób, aby każda prosta była jednokolorowa lub dwukolorowa. Jaka jest największa możliwa liczba kolorów, których można użyć do pomalowania punktów tej płaszczyzny? Odpowiedź uzasadnij.
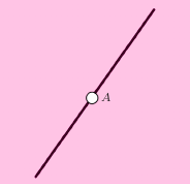
Rys. 2
Odpowiedź brzmi: trzy kolory. Udowodnijmy najpierw nie wprost, że nie możemy użyć czterech kolorów. Załóżmy, że można użyć czterech kolorów - wybierzmy zatem cztery różnokolorowe punkty. Zauważmy, że żadne trzy z nich nie są współliniowe, bo w innym przypadku znaleźlibyśmy trzykolorową prostą. Oznaczmy wybrane przez nas punkty 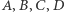 w taki sposób, by proste
w taki sposób, by proste 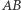 i
i 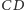 się przecinały. Ich wspólny punkt oznaczmy jako
się przecinały. Ich wspólny punkt oznaczmy jako 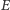 (Rys. 1). Jeśli punkt
(Rys. 1). Jeśli punkt 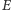 ma taki sam kolor co punkt
ma taki sam kolor co punkt 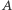 czy
czy 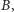 to prosta
to prosta 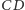 jest trzykolorowa. W innym przypadku prosta
jest trzykolorowa. W innym przypadku prosta 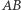 jest trzykolorowa. Dowiedliśmy, że kolorując płaszczyznę przy użyciu czterech kolorów, zawsze znajdziemy trzykolorową prostą. Teraz pokażę kolorowanie płaszczyzny trzema kolorami, spełniające warunki zadania. Pokolorujmy całą płaszczyznę jednym kolorem, np. zielonym. Wybierzmy dowolną prostą i pokolorujmy ją innym kolorem, np. niebieskim. Na prostej wybierzmy dowolny punkt i pokolorujmy go trzecim kolorem, np. czerwonym. Wtedy każda prosta jest co najwyżej dwukolorowa (Rys. 2).
jest trzykolorowa. Dowiedliśmy, że kolorując płaszczyznę przy użyciu czterech kolorów, zawsze znajdziemy trzykolorową prostą. Teraz pokażę kolorowanie płaszczyzny trzema kolorami, spełniające warunki zadania. Pokolorujmy całą płaszczyznę jednym kolorem, np. zielonym. Wybierzmy dowolną prostą i pokolorujmy ją innym kolorem, np. niebieskim. Na prostej wybierzmy dowolny punkt i pokolorujmy go trzecim kolorem, np. czerwonym. Wtedy każda prosta jest co najwyżej dwukolorowa (Rys. 2).
Po zawodach zadałam sobie następujące pytanie. Załóżmy, że każda prosta jest co najwyżej trzykolorowa. Jak wiele kolorów mogliśmy wtedy użyć do pokolorowania punktów płaszczyzny? Odpowiedź jest w tym przypadku zaskakująca: mogliśmy użyć nieskończenie wiele kolorów! Pokolorujmy całą płaszczyznę jednym kolorem. Wybierzmy dowolny okrąg i pokolorujmy każdy jego punkt innym kolorem. Jeśli prosta nie ma punktów wspólnych z okręgiem, jest jednokolorowa. Jeśli jest do niego styczna, jest dwukolorowa, a jeśli prosta przecina okrąg, jest trzykolorowa. Możemy postawić analogiczne pytania dla okręgów: na ile kolorów możemy pokolorować punkty płaszczyzny, jeśli każdy okrąg może być co najwyżej dwu- czy trzykolorowy. Rozwiązania tych problemów są bardzo podobne do tych postawionych dla prostych, dlatego znalezienie odpowiedzi pozostawiam Czytelnikowi.
Moja praca odpowiada na jeszcze bardziej złożone pytanie niż to postawione podczas olimpiady: na ile kolorów można pokolorować punkty płaszczyzny, jeśli każda prosta może być co najwyżej 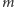 -kolorowa, a każdy okrąg co najwyżej
-kolorowa, a każdy okrąg co najwyżej  -kolorowy. W pracy udało mi się znaleźć odpowiedź dla prawie wszystkich wartości
-kolorowy. W pracy udało mi się znaleźć odpowiedź dla prawie wszystkich wartości  i
i  - wyjątkiem jest przypadek
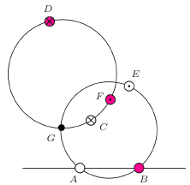
- wyjątkiem jest przypadek 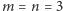 - umiem pokazać, że w takim przypadku możemy użyć czterech kolorów, ale nie sześciu. W dalszej części artykułu zaprezentuję dowody dotyczące tego problemu. Przypadek pięciu kolorów jest otwarty.
- umiem pokazać, że w takim przypadku możemy użyć czterech kolorów, ale nie sześciu. W dalszej części artykułu zaprezentuję dowody dotyczące tego problemu. Przypadek pięciu kolorów jest otwarty.
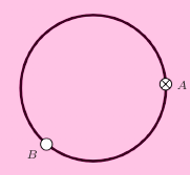
Rys. 3
Twierdzenie. Niech 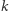 będzie maksymalną liczbą kolorów, na które możemy pokolorować punkty płaszczyzny tak, że każda prosta i każdy okrąg będą co najwyżej trzykolorowe. Wtedy
będzie maksymalną liczbą kolorów, na które możemy pokolorować punkty płaszczyzny tak, że każda prosta i każdy okrąg będą co najwyżej trzykolorowe. Wtedy 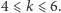
Na początku pokażę kolorowanie płaszczyzny czterema kolorami, takie, że każda prosta i każdy okrąg są co najwyżej trzykolorowe. Pokolorujmy całą płaszczyznę jednym kolorem, np. fioletowym. Wybierzemy okrąg i pokolorujmy go innym kolorem, np. brązowym. Na okręgu wybierzmy dwa punkty i pokolorujmy je na jeszcze inne kolory, np. czerwony i zielony. Wtedy każdy okrąg i każda prosta będą co najwyżej trzykolorowe (Rys. 3). Stąd 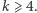
Załóżmy teraz, że możemy pokolorować płaszczyznę sześcioma kolorami - wybierzmy sześć różnokolorowych punktów. Zauważmy, że możemy znaleźć prostą przechodzącą przez co najmniej dwa punkty, taką że pozostałe wybrane punkty będą leżeć po jednej stronie tej prostej. Z drugiej strony zauważmy, że na takiej prostej mogą leżeć co najwyżej trzy wybrane punkty, bo w innym przypadku znaleźlibyśmy czterokolorową prostą. Rozpatrujemy zatem dwa przypadki ze względu na liczbę wyróżnionych punktów na wybranej prostej. Poniżej przedstawię jeden z nich (rozumowanie dla drugiego z nich jest analogiczne i pozostawiam je Czytelnikowi).
Rys. 4
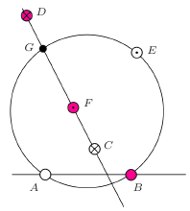
Rys. 5
Załóżmy, że na prostej leżą dokładnie dwa wybrane punkty - oznaczmy je jako 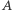 i
i 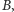 a pozostałe jako
a pozostałe jako 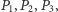 i
i 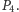 Spośród kątów
Spośród kątów 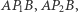
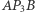 i
i 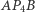 wybierzmy ten o największej mierze -
wybierzmy ten o największej mierze - 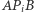 (zauważmy, że gdyby były dwa takie kąty, to znaleźlibyśmy czterokolorowy okrąg). Punkt
(zauważmy, że gdyby były dwa takie kąty, to znaleźlibyśmy czterokolorowy okrąg). Punkt 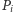 oznaczmy jako
oznaczmy jako 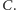 Spośród pozostałych kątów wybierzmy ten o minimalnej mierze -
Spośród pozostałych kątów wybierzmy ten o minimalnej mierze - 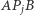 (jest tylko jeden taki kąt). Punkt
(jest tylko jeden taki kąt). Punkt 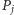 oznaczmy jako
oznaczmy jako 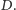 Pozostałe punkty oznaczmy jako
Pozostałe punkty oznaczmy jako 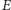 i
i 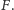 Zauważmy, że punkt
Zauważmy, że punkt 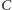 leży wewnątrz okręgu
leży wewnątrz okręgu 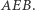 Rozpatrzmy teraz dwa przypadki:
Rozpatrzmy teraz dwa przypadki:
- Punkty
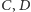 i
i 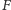 są współliniowe. Jeden z punktów przecięcia prostej
są współliniowe. Jeden z punktów przecięcia prostej 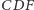 z okręgiem
z okręgiem 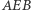 oznaczam jako
oznaczam jako 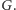 Jeśli punkt
Jeśli punkt 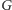 ma taki sam kolor co któryś z punktów
ma taki sam kolor co któryś z punktów 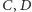 lub
lub 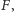 to okrąg
to okrąg 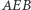 jest czterokolorowy. W innym przypadku prosta
jest czterokolorowy. W innym przypadku prosta 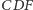 jest czterokolorowa (Rys. 4).
jest czterokolorowa (Rys. 4). - Punkty
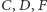 nie są współliniowe. Jeden z punktów przecięcia okręgu
nie są współliniowe. Jeden z punktów przecięcia okręgu 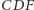 z okręgiem
z okręgiem 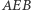 oznaczam jako
oznaczam jako 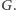 Jeśli punkt
Jeśli punkt 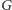 ma taki sam kolor co któryś z punktów
ma taki sam kolor co któryś z punktów 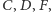 to okrąg
to okrąg 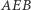 jest trzykolorowy. W innym przypadku okrąg
jest trzykolorowy. W innym przypadku okrąg 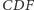 jest trzykolorowy (Rys. 5).
jest trzykolorowy (Rys. 5).
W każdym przypadku (także dla trzech wybranych punktów na prostej) znajdujemy czterokolorową prostą lub okrąg. Zatem nie możemy wykorzystać sześciu kolorów do pokolorowania punktów płaszczyzny w taki sposób, żeby każda prosta i każdy okrąg były co najwyżej trzykolorowe. Zatem 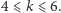 Co ciekawe, w przypadku gdy kolorujemy punkty płaszczyzny z zachowaniem warunku, że każda prosta jest co najwyżej trzykolorowa, a każdy okrąg co najwyżej czterokolorowy, możemy użyć nieskończenie wielu kolorów. Aby to wykazać, potrzebujemy następującego lematu:
Co ciekawe, w przypadku gdy kolorujemy punkty płaszczyzny z zachowaniem warunku, że każda prosta jest co najwyżej trzykolorowa, a każdy okrąg co najwyżej czterokolorowy, możemy użyć nieskończenie wielu kolorów. Aby to wykazać, potrzebujemy następującego lematu:
Lemat. Istnieje taki zbiór punktów 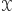 o nieskończonej liczbie elementów, że żadne trzy punkty należące do
o nieskończonej liczbie elementów, że żadne trzy punkty należące do 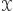 nie leżą na jednej prostej i żadne cztery nie leżą na jednym okręgu.
nie leżą na jednej prostej i żadne cztery nie leżą na jednym okręgu.
Zdefiniujmy przez indukcję ciąg zbiorów 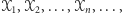 które spełniają następujące warunki:
które spełniają następujące warunki:
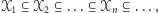
- dla każdego
 żadne trzy punkty należące do zbioru
żadne trzy punkty należące do zbioru 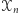 nie są współliniowe,
nie są współliniowe, - dla każdego
 żadne cztery punkty należące do zbioru
żadne cztery punkty należące do zbioru 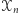 nie leżą na jednym okręgu,
nie leżą na jednym okręgu, - zbiór
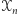 zawiera
zawiera 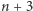 punkty.
punkty.
Zbiór 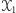 zawiera wierzchołki dowolnego trójkąta i jego ortocentrum, zatem spełnia wszystkie żądane warunki. Nowy zbiór
zawiera wierzchołki dowolnego trójkąta i jego ortocentrum, zatem spełnia wszystkie żądane warunki. Nowy zbiór 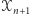 ze zbioru
ze zbioru 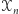 tworzymy w następujący sposób: przez każde dwa punkty zbioru
tworzymy w następujący sposób: przez każde dwa punkty zbioru 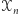 prowadzimy prostą, a przez każde trzy okrąg. Niech narysowane obiekty tworzą razem zbiór
prowadzimy prostą, a przez każde trzy okrąg. Niech narysowane obiekty tworzą razem zbiór 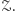 Zauważmy, że liczba prostych i okręgów jest skończona. Wybierzmy prostą, która nie należy do zbioru
Zauważmy, że liczba prostych i okręgów jest skończona. Wybierzmy prostą, która nie należy do zbioru 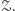 Proste i okręgi przecinają ją w skończonej liczbie punktów. Wybierzmy zatem punkt
Proste i okręgi przecinają ją w skończonej liczbie punktów. Wybierzmy zatem punkt 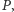 który nie leży na żadnej prostej czy okręgu należącym do zbioru
który nie leży na żadnej prostej czy okręgu należącym do zbioru 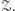 Wtedy
Wtedy 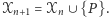 Rozważmy zbiór
Rozważmy zbiór 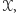 będący sumą wszystkich zbiorów
będący sumą wszystkich zbiorów 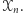 Zauważmy, że zbiór
Zauważmy, że zbiór 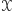 zawiera nieskończenie wiele elementów. Ponadto żadne trzy punkty należące do tego zbioru nie są współliniowe, a żadne cztery nie leżą na jednym okręgu. Zatem zbiór
zawiera nieskończenie wiele elementów. Ponadto żadne trzy punkty należące do tego zbioru nie są współliniowe, a żadne cztery nie leżą na jednym okręgu. Zatem zbiór 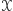 jest szukanym przez nas zbiorem.
jest szukanym przez nas zbiorem.

Jak, mając taki zbiór, możemy pokolorować płaszczyznę tak, by każda prosta była co najwyżej trzykolorowa, a każdy okrąg co najwyżej czterokolorowy? Pokolorujmy całą płaszczyznę jednym kolorem. Następnie weźmy taki zbiór punktów 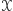 o nieskończonej liczbie elementów, że żadne trzy punkty, które do niego należą, nie są współliniowe, żadne cztery nie leżą na jednym okręgu. Każdy punkt należący do zbioru
o nieskończonej liczbie elementów, że żadne trzy punkty, które do niego należą, nie są współliniowe, żadne cztery nie leżą na jednym okręgu. Każdy punkt należący do zbioru 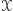 pokolorujmy innym kolorem. Wtedy każda prosta będzie co najwyżej trzykolorowa, a każdy okrąg co najwyżej czterokolorowy. Rozwinięte zadanie z Olimpiady Matematycznej Juniorów okazało się bardzo ciekawym problemem. Obecnie pracuję nad jego uogólnieniem w trzecim wymiarze.
pokolorujmy innym kolorem. Wtedy każda prosta będzie co najwyżej trzykolorowa, a każdy okrąg co najwyżej czterokolorowy. Rozwinięte zadanie z Olimpiady Matematycznej Juniorów okazało się bardzo ciekawym problemem. Obecnie pracuję nad jego uogólnieniem w trzecim wymiarze.
Kończąc, chciałabym bardzo podziękować opiekunowi mojej pracy, Panu Wojciechowi Guzickiemu za zaproponowanie mi tego tematu oraz pomoc przy tworzeniu pracy.