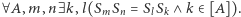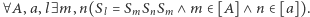Uczniowie
W 1967 roku szkoła podstawowa wypuściła po raz pierwszy absolwentów ośmioletniej podstawówki (tak, kiedyś też były reformy szkolne). W ogólnym reformatorskim zamieszaniu można było zrobić coś nietypowego, więc Wydział Matematyki i Fizyki Uniwersytetu Warszawskiego uruchomił uniwersyteckie klasy matematyczno-fizyczne w liceum im. Klementa Gottwalda (w latach 1906-50 oraz po 1990 roku Stanisława Staszica) - pretekst był prosty: pierwszym dyrektorem tego liceum był Jan Zydler, znakomity nauczyciel matematyki i autor do dziś niezapomnianych podręczników geometrii.
Sprawie patronował profesor Stanisław Mazur, a organizatorem była pełna niewyczerpywalnej energii Hanna Szmuszkowicz.
W jednej z pierwszych klas uczyłem geometrii (bo klasy były dwie, a geometrii uczył także Jerzy Lisiewicz, algebry zaś Juliusz Brzeziński i Maciej Bryński - byliśmy przekonani, że skoro uczymy nauczycieli, to powinniśmy sami też zobaczyć, jak się to robi).
Na wiosnę 1969 roku przydarzyła mi się fantastyczna historia, którą chcę przypomnieć, bo w lipcu 2016 dowiedziałem się, że już obaj jej bohaterowie nie żyją.
Owi bohaterowie to uczniowie drugiej klasy liceum (czyli szesnastolatkowie): Jerzy Zabilski, później matematyk (zmarły w 2011 roku) i Wiesław Mielniczuk, później fizyk (zmarły w 2016 roku - dziwna jest ta kolejność naszego znikania).
W klasie zadaję zadanie:
Zadanie 1. Wykazać, że dowolną izometrię płaszczyzny można uzyskać ze złożenia symetrii względem prostych należących do jednego pęku właściwego oraz jednego pęku niewłaściwego.
Zadanie to klasa zbiorowo rozwiązuje (Czytelniku, rozwiąż i Ty), więc proponuję zadanie domowe:
Zadanie 2. Wykazać, że dowolną izometrię płaszczyzny można uzyskać ze złożenia symetrii względem prostych należących do jednego pęku właściwego plus jedna prosta spoza tego pęku.
Czworo uczniów odpowiedziało twierdząco. Wobec tego zaproponowałem pytanie dodatkowe: jaki jest rząd generowania grupy izometrii w pierwszym i drugim przypadku?
Tu niezbędne jest wyjaśnienie: nie wiedziałem, jaki jest wynik, ani nawet nie miałem pomysłu, jak się do tego zabrać (mój współnauczyciel też nie, a myślę, że wielu nie tylko wtedy, ale i do dziś nie wie).
Tymczasem moi dwaj bohaterowie podali wynik: 4 i 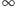 ; i tym sposobem, jako nieletni uzyskali poważną publikację (Wiadomości Matematyczne XIII (1971), pp. 37-41) z rekomendacji profesora Stefana Straszewicza, twórcy olimpiad matematycznych.
; i tym sposobem, jako nieletni uzyskali poważną publikację (Wiadomości Matematyczne XIII (1971), pp. 37-41) z rekomendacji profesora Stefana Straszewicza, twórcy olimpiad matematycznych.
A oto, jak uzyskali swoje rezultaty.
Twierdzenie. Do uzyskania wszystkich izometrii płaszczyzny wystarczą symetrie o osiach z ![[A]](/math/temat/matematyka/geometria/planimetria/2016/12/28/Uczniowie/1x-27ad00d699075f8852a446e7a797bb1592927e59-im-33,33,33-FF,FF,FF.gif) gdzie
gdzie ![a /∈ [A].](/math/temat/matematyka/geometria/planimetria/2016/12/28/Uczniowie/2x-27ad00d699075f8852a446e7a797bb1592927e59-im-33,33,33-FF,FF,FF.gif)
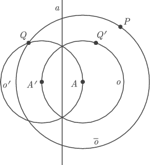
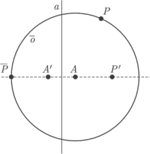
Dowód. Ponieważ izometria mająca punkt stały to obrót względem tego punktu lub symetria względem prostej przechodzącej przez ten punkt (a to mamy, bo możemy używać symetrii względem wszystkich prostych z ![[A] |](/math/temat/matematyka/geometria/planimetria/2016/12/28/Uczniowie/1x-fd28489bf392a4cf2fcfa3877d4549fa908993a9-im-33,33,33-FF,FF,FF.gif) ), wystarczy wykazać, że dowolny punkt
), wystarczy wykazać, że dowolny punkt 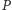 można nałożyć na
można nałożyć na 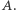 Przypadek 1:
Przypadek 1: 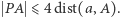
Odbijamy 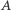 względem
względem 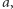 otrzymując
otrzymując 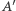 i rysujemy okrąg o środku
i rysujemy okrąg o środku 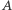 i promieniu
i promieniu 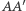 - oznaczmy go
- oznaczmy go 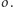 Obraz okręgu
Obraz okręgu  w symetrii względem
w symetrii względem  oznaczmy przez
oznaczmy przez 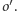 Okrąg
Okrąg 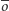 o środku
o środku 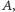 poprowadzony przez
poprowadzony przez 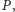 przecina okrąg
przecina okrąg 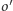 (założenie!) w punkcie
(założenie!) w punkcie 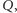 więc możemy
więc możemy 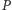 przeprowadzić na
przeprowadzić na 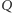 za pomocą symetrii z
za pomocą symetrii z ![[A]. |](/math/temat/matematyka/geometria/planimetria/2016/12/28/Uczniowie/21x-fd28489bf392a4cf2fcfa3877d4549fa908993a9-im-33,33,33-FF,FF,FF.gif) Obraz
Obraz 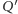 punktu
punktu 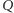 w symetrii względem
w symetrii względem 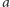 leży na
leży na 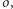 więc może być przez symetrię względem prostej z
więc może być przez symetrię względem prostej z ![[A]](/math/temat/matematyka/geometria/planimetria/2016/12/28/Uczniowie/26x-fd28489bf392a4cf2fcfa3877d4549fa908993a9-im-33,33,33-FF,FF,FF.gif) (konkretnie: symetralnej
(konkretnie: symetralnej 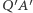 ) przeprowadzony na
) przeprowadzony na 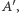 a stąd przez symetrię względem
a stąd przez symetrię względem 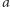 na
na 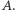
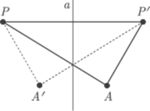
Przypadek 2: 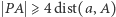
sprowadza się do przypadku 1: przez symetrię względem dwusiecznej 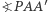 punkt
punkt 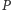 przechodzi na
przechodzi na 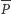 i przez symetrię względem
i przez symetrię względem 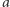 na
na 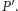 Ponieważ
Ponieważ
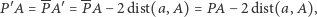
więc odległość od punktu 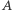 zmniejszyła się o
zmniejszyła się o 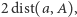 co powtarzane wielokrotnie (na załączonym obrazku widać, że gdy musimy wykonać więcej kroków niż jeden, kolejny zaczyna się od prostej z
co powtarzane wielokrotnie (na załączonym obrazku widać, że gdy musimy wykonać więcej kroków niż jeden, kolejny zaczyna się od prostej z ![[A]](/math/temat/matematyka/geometria/planimetria/2016/12/28/Uczniowie/10x-e121eb6cb0ae1f73f57a0264e1bc0c88197a0e14-im-33,33,33-FF,FF,FF.gif) równoległej do
równoległej do  ) daje spełnienie warunku z przypadku 1.
) daje spełnienie warunku z przypadku 1.
Stwierdzenie, że rząd generowania jest w tym przypadku nieskończony, nawiązuje do rozważenia przypadku 2 - tam przybliżaliśmy punkt 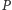 do punktu
do punktu 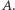 Zauważmy, że to przybliżanie nie może być wykonane większymi niż tam krokami.
Zauważmy, że to przybliżanie nie może być wykonane większymi niż tam krokami.
Symetrie względem prostych z ![[A] |](/math/temat/matematyka/geometria/planimetria/2016/12/28/Uczniowie/1x-c6fce7f90f8cac30f64f6b064b6996cd197e9034-im-33,33,33-FF,FF,FF.gif) nie przybliżają bowiem punktów do
nie przybliżają bowiem punktów do 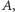 symetria zaś względem
symetria zaś względem 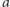 przybliża punkty nie więcej niż o
przybliża punkty nie więcej niż o 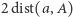 :
:
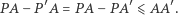
A ponieważ możemy punkt 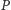 obrać dowolnie daleko, więc izometria nakładająca go na
obrać dowolnie daleko, więc izometria nakładająca go na 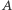 może wymagać dowolnie wielu symetrii - rząd zatem jest nieskończony.
może wymagać dowolnie wielu symetrii - rząd zatem jest nieskończony.
Tyle o przypadku, gdy osie symetrii były wybierane z ![[A] |](/math/temat/matematyka/geometria/planimetria/2016/12/28/Uczniowie/1x-5655e5f994749b89af9ae3000d08b7e825ca7868-im-33,33,33-FF,FF,FF.gif) dla
dla ![|a /∈ [A].](/math/temat/matematyka/geometria/planimetria/2016/12/28/Uczniowie/2x-5655e5f994749b89af9ae3000d08b7e825ca7868-im-33,33,33-FF,FF,FF.gif)
Pozostaje wykazanie, że
Twierdzenie. Rząd generowania dla prostych z ![[A] |](/math/temat/matematyka/geometria/planimetria/2016/12/28/Uczniowie/1x-14a23f2d2147d1ab953ab278da24852852f484f3-im-33,33,33-FF,FF,FF.gif) jest równy 4.
jest równy 4.
Dowód ma charakter raczej algebraiczny. Potrzebne są dwa lematy:
Dowód lematu jest oczywisty. Istotnie, gdy 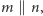 jako
jako 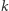 obieramy równoległą do
obieramy równoległą do  i przechodzącą przez
i przechodzącą przez 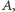 a
a 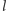 równoległą do niej i leżącą względem niej tak, jak
równoległą do niej i leżącą względem niej tak, jak  względem
względem 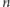 - wtedy oba złożenia są tym samym przesunięciem; gdy z kolei
- wtedy oba złożenia są tym samym przesunięciem; gdy z kolei  i
i  mają wspólny punkt
mają wspólny punkt 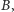 bierzemy jako
bierzemy jako 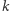 prostą
prostą 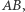 a
a 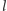 przez
przez 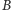 leżącą tak, jak
leżącą tak, jak 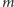 względem
względem 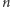 - wtedy oba złożenia są tym samym obrotem.
- wtedy oba złożenia są tym samym obrotem.
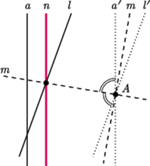
Drugi lemat nie jest już tak oczywisty
Tutaj najpierw przez 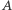 prowadzimy
prowadzimy 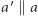 i
i 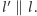 Jako
Jako 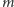 bierzemy dowolną z dwusiecznych kąta
bierzemy dowolną z dwusiecznych kąta 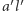 i przez jej przecięcie z
i przez jej przecięcie z 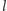 prowadzimy
prowadzimy 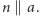 Prosta
Prosta 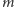 jest wtedy dwusieczną kąta
jest wtedy dwusieczną kąta 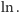 Stąd
Stąd 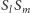 i
i 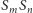 realizują ten sam obrót, a równość
realizują ten sam obrót, a równość 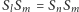 to właśnie (2).
to właśnie (2).
Mając takie lematy, nie natrafia się już na żadne trudności.
Dowolna izometria 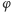 jest (jak to już przypomniałem) złożeniem dwóch lub trzech symetrii osiowych, co rozpatrujemy kolejno.
jest (jak to już przypomniałem) złożeniem dwóch lub trzech symetrii osiowych, co rozpatrujemy kolejno.
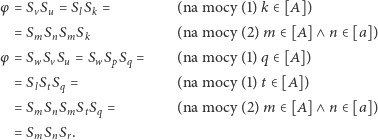
Ostatnia równość bierze się stąd, że 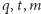 są współpękowe, a symetrie względem trzech prostych współpekowych zawsze można zastąpić jedną (co bez trudu można zauważyć również w argumentacji przy (1)).
są współpękowe, a symetrie względem trzech prostych współpekowych zawsze można zastąpić jedną (co bez trudu można zauważyć również w argumentacji przy (1)).
Zaskakujące jest, że nadal do uzyskania izometrii zmieniających orientację potrzeba, tak jak i bez ograniczenia wyboru osi symetrii, jedynie trzech symetrii osiowych.
Takich miałem uczniów. Szkoda, że już ich nie spotkam.