Pewne uogólnienie prostej Eulera
Panuje przekonanie, że w niemodnej obecnie dziedzinie geometrii klasycznej wszystko jest znane i nie pozostało nic do odkrycia. Kłam temu stwierdzeniu zadaje dość ciekawe i (jeszcze) mało znane twierdzenie, które przedstawiamy w niniejszym artykule. Warto zaznaczyć, że środki, jakie posłużyły nam do dowodu, są czysto geometryczne i nie korzystają z narzędzi analitycznych. Aby ułatwić jego zrozumienie, przedstawiamy najpierw pewne pojęcia, definicje i bardziej znane fakty powiązane z tym zagadnieniem.
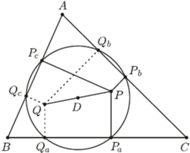
Definicja. Trójkątem spodkowym punktu  wewnątrz trójkąta
wewnątrz trójkąta  nazywamy trójkąt, którego wierzchołkami są rzuty prostokątne punktu
nazywamy trójkąt, którego wierzchołkami są rzuty prostokątne punktu  na boki trójkąta
na boki trójkąta 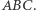
Wykażemy teraz, że dla każdego trójkąta spodkowego można wskazać pewien "stowarzyszony" z nim trójkąt spodkowy.
Lemat 1. Niech 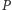 będzie dowolnym punktem wewnątrz trójkąta
będzie dowolnym punktem wewnątrz trójkąta 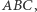 a
a 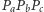 jego trójkątem spodkowym. Okrąg opisany na trójkącie
jego trójkątem spodkowym. Okrąg opisany na trójkącie  przecina boki
przecina boki 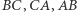 dodatkowo w punktach
dodatkowo w punktach 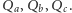 Wtedy
Wtedy 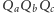 też jest trójkątem spodkowym dla pewnego punktu leżącego wewnątrz trójkąta
też jest trójkątem spodkowym dla pewnego punktu leżącego wewnątrz trójkąta 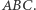
Dowód. Niech 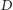 będzie środkiem okręgu opisanego na trójkącie
będzie środkiem okręgu opisanego na trójkącie 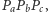 a
a 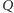 punktem symetrycznym do punktu
punktem symetrycznym do punktu  względem
względem  Z oczywistych powodów
Z oczywistych powodów 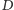 należy do symetralnej odcinka
należy do symetralnej odcinka 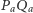 oraz
oraz 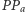 jest prostopadły do
jest prostopadły do 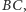 więc
więc 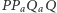 jest trapezem. To oznacza, że
jest trapezem. To oznacza, że 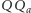 jest prostopadły do
jest prostopadły do  Analogicznie otrzymujemy, że
Analogicznie otrzymujemy, że 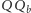 i
i  są prostopadłe odpowiednio do
są prostopadłe odpowiednio do 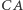 i
i 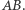 Inaczej mówiąc,
Inaczej mówiąc, 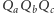 jest trójkątem spodkowym punktu
jest trójkątem spodkowym punktu 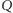 względem trójkąta
względem trójkąta 
Zauważmy, że na czworokątach 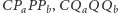 i
i 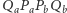 można opisać okręgi, a zatem
można opisać okręgi, a zatem
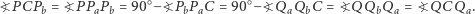 |
Analogicznie pokazujemy, że 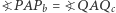 i
i 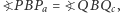 co oznacza, że punkty
co oznacza, że punkty 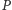 i
i 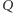 są izogonalnie sprzężone w trójkącie
są izogonalnie sprzężone w trójkącie 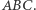 Zauważmy też, że jeśli
Zauważmy też, że jeśli  nie jest środkiem okręgu wpisanego, to
nie jest środkiem okręgu wpisanego, to 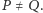 Poniżej przedstawiamy pewną własność prostej przechodzącej przez punkty izogonalnie sprzężone w dowolnym trójkącie.
Poniżej przedstawiamy pewną własność prostej przechodzącej przez punkty izogonalnie sprzężone w dowolnym trójkącie.
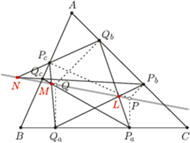
Stwierdzenie 1. Niech 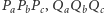 będą trójkątami spodkowymi punktów
będą trójkątami spodkowymi punktów  i
i 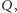 leżących wewnątrz trójkąta
leżących wewnątrz trójkąta 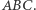 Punkty przecięcia prostych
Punkty przecięcia prostych 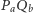 i
i 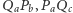 i
i  oraz
oraz 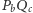 i
i 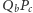 oznaczamy odpowiednio jako
oznaczamy odpowiednio jako 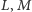 i
i 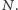 Wówczas jeśli punkty
Wówczas jeśli punkty 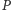 i
i 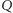 są izogonalnie sprzężone, to punkty
są izogonalnie sprzężone, to punkty  leżą na prostej przechodzącej przez
leżą na prostej przechodzącej przez  i
i 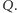
Dowód. Niech  i
i  Wówczas na czworokącie
Wówczas na czworokącie  można opisać okrąg. Ponadto z wcześniejszych rozważań wynika, że na czworokącie
można opisać okrąg. Ponadto z wcześniejszych rozważań wynika, że na czworokącie 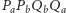 również można opisać okrąg. W tej sytuacji
również można opisać okrąg. W tej sytuacji

więc 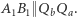 Mamy również
Mamy również 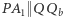 (oba są prostopadłe do
(oba są prostopadłe do 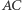 ),
), 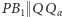 (oba są prostopadłe do
(oba są prostopadłe do  ), co oznacza, że trójkąty
), co oznacza, że trójkąty 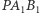 i
i 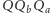 są jednokładne, zatem proste łączące odpowiadające pary wierzchołków przecinają się w jednym punkcie, skąd wnioskujemy, że
są jednokładne, zatem proste łączące odpowiadające pary wierzchołków przecinają się w jednym punkcie, skąd wnioskujemy, że 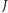 należy do prostej
należy do prostej 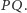 Następnie, stosując twierdzenie Pappusa dla dwóch układów potrójnych punktów współliniowych
Następnie, stosując twierdzenie Pappusa dla dwóch układów potrójnych punktów współliniowych 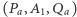 i
i 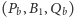 z uwagą, że
z uwagą, że 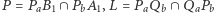 i
i 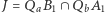 wnioskujemy, że
wnioskujemy, że 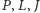 są współliniowe. Wiemy więc, że
są współliniowe. Wiemy więc, że 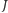 leży na prostej
leży na prostej 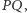 a
a 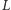 leży na prostej
leży na prostej 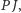 zatem
zatem 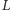 leży na prostej
leży na prostej 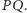 Analogicznie dowodzimy, że punkty
Analogicznie dowodzimy, że punkty 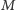 i
i  leżą na prostej
leżą na prostej 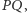 co kończy dowód lematu.
co kończy dowód lematu.
Rzutowanie punktu na boki to nie jedyny naturalny sposób na konstrukcję "nowego" trójkąta. Inny prezentuje poniższa definicja.
Definicja. Trójkątem Cevy punktu 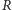 leżącego wewnątrz trójkąta
leżącego wewnątrz trójkąta  nazywamy trójkąt
nazywamy trójkąt 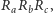 gdzie
gdzie 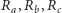 są punktami przecięcia prostych
są punktami przecięcia prostych 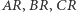 odpowiednio z bokami
odpowiednio z bokami 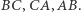
Okazuje się, że dla trójkąta Cevy również prawdziwy jest fakt wykazany wcześniej dla trójkąta spodkowego.
Lemat 2. Niech 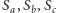 będą punktami przecięcia okręgu opisanego na trójkącie Cevy
będą punktami przecięcia okręgu opisanego na trójkącie Cevy 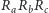 wewnątrz trójkąta
wewnątrz trójkąta 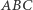 odpowiednio z bokami
odpowiednio z bokami 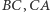 i
i 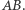 Wtedy proste
Wtedy proste  i
i 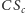 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Dowód. Zgodnie z twierdzeniem Cevy, skoro proste  przecinają się w punkcie
przecinają się w punkcie 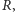 zachodzi
zachodzi

Ponieważ  i
i  należą do wspólnego okręgu, więc z twierdzenia o potędze punktu względem okręgu mamy
należą do wspólnego okręgu, więc z twierdzenia o potędze punktu względem okręgu mamy

Stąd

Podstawiając te wartości do pierwszego równania, otrzymujemy

Ostatnia równość, zgodnie z odwrotnym twierdzeniem Cevy, dowodzi, że 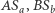 i
i 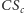 zbiegają się w jednym punkcie.
zbiegają się w jednym punkcie.

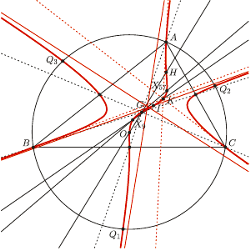
Krzywa trzeciego stopnia Darboux
Powyższe rozważania pokazują, że dla każdego punktu 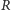 wewnątrz trójkąta
wewnątrz trójkąta 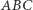 istnieje dokładnie jeden "stowarzyszony" z nim punkt
istnieje dokładnie jeden "stowarzyszony" z nim punkt 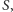 będący punktem przecięcia prostych
będący punktem przecięcia prostych  i
i 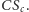 Prostą przechodzącą przez te dwa punkty nazywamy osią Cevy. Niżej przedstawiamy ciekawą własność osi Cevy:
Prostą przechodzącą przez te dwa punkty nazywamy osią Cevy. Niżej przedstawiamy ciekawą własność osi Cevy:
Stwierdzenie 2. Niech 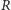 i
i  będą dwoma stowarzyszonymi punktami Cevy wewnątrz trójkąta
będą dwoma stowarzyszonymi punktami Cevy wewnątrz trójkąta 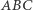 i niech odpowiadają im trójkąty Cevy
i niech odpowiadają im trójkąty Cevy 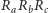 i
i  Niech
Niech 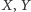 i
i 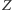 będą odpowiednio punktami przecięcia prostych
będą odpowiednio punktami przecięcia prostych 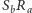 i
i 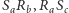 i
i 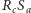 oraz
oraz  i
i 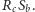 Wówczas punkty
Wówczas punkty  są współliniowe (tworzą oś Cevy
są współliniowe (tworzą oś Cevy 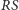 ).
).
Dowód. Stosując twierdzenie Pappusa dla dwóch potrójnych układów punktów współliniowych 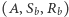 i
i  z uwagą, że
z uwagą, że 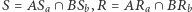 i
i  wnioskujemy, że
wnioskujemy, że 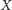 leży na prostej
leży na prostej 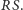 Analogicznie dowodzimy, że punkty
Analogicznie dowodzimy, że punkty  i
i 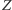 leżą na prostej
leżą na prostej 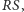 co kończy dowód lematu.
co kończy dowód lematu.
Nasze dotychczasowe zmagania dotyczyły dwóch trójkątów, spodkowego i Cevy. Z każdym z nich związaliśmy pewną oś, wskazując szczególne punkty, które się na niej znajdują. Jesteśmy już gotowi na to, by zająć się trójkątami, które są jednocześnie trójkątami spodkowymi i trójkątami Cevy.
Definicja. Jeśli spodkowy trójkąt punktu  jest również trójkątem Cevy, to punkt
jest również trójkątem Cevy, to punkt  nazywamy czewiańskim punktem spodkowym (ang. pedal-cevian point).
nazywamy czewiańskim punktem spodkowym (ang. pedal-cevian point).
Wiele właściwości tych punktów można znaleźć w pracach Darboux. Jednym z jego znanych wyników, uzyskanych metodami algebraicznymi, jest dowód, że czewiańskie punkty spodkowe ustalonego trójkąta tworzą tzw. krzywą trzeciego stopnia Darboux; jest ich zatem nieskończenie wiele.
Zapewne wśród osób zainteresowanych geometrią wiele nieraz miało do czynienia z zadaniami dotyczącymi czewiańskich punktów spodkowych. Przykładami takich punktów w dowolnym trójkącie są m.in. jego ortocentrum, środek ciężkości, środek okręgu wpisanego i środek okręgu opisanego.
Chcielibyśmy teraz przedstawić pewną ciekawą własność czewiańskich punktów spodkowych. Nie udało się nam odnaleźć publikacji przedstawionego rezultatu, więc jest niemała szansa na to, że to wynik całkiem nowy. Niezależnie od słuszności naszych przypuszczeń, uważamy, że każdy miłośnik geometrii doceni jego elegancję!
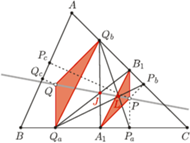
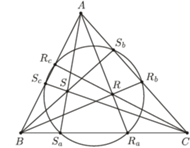
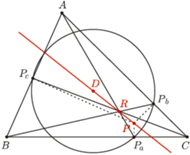
Twierdzenie. Niech  będzie trójkątem spodkowym punktu
będzie trójkątem spodkowym punktu 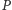 wewnątrz trójkąta
wewnątrz trójkąta 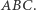 Dodatkowo zakładamy, że
Dodatkowo zakładamy, że 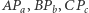 przecinają się w punkcie
przecinają się w punkcie  Wtedy punkty
Wtedy punkty 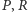 i środek okręgu opisanego na
i środek okręgu opisanego na 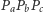 leżą na jednej prostej.
leżą na jednej prostej.
Dowód. Niech  będzie środkiem okregu opisanego na
będzie środkiem okregu opisanego na 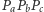 i niech punkty
i niech punkty  będą zdefiniowane tak, jak w stwierdzeniu 1. Zgodnie z tym stwierdzeniem punkty te są współliniowe, a prosta przez nie przechodząca zawiera również punkty
będą zdefiniowane tak, jak w stwierdzeniu 1. Zgodnie z tym stwierdzeniem punkty te są współliniowe, a prosta przez nie przechodząca zawiera również punkty 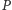 i
i 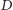 (jest to oś trójkąta spodkowego dla punktu
(jest to oś trójkąta spodkowego dla punktu 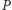 ). Prosta ta jest jednak również osią trójkąta Cevy punktu
). Prosta ta jest jednak również osią trójkąta Cevy punktu 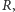 zatem zgodnie ze stwierdzeniem 2 przechodzi przez
zatem zgodnie ze stwierdzeniem 2 przechodzi przez 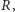 co dowodzi współliniowości punktów
co dowodzi współliniowości punktów 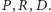
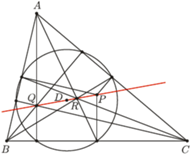
Zastanówmy się, czym skutkować będzie powyższe stwierdzenie, jeśli za punkt 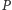 przyjmiemy środek okręgu opisanego na trójkącie
przyjmiemy środek okręgu opisanego na trójkącie 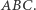 Okazuje się, że wówczas okrąg opisany na punktach
Okazuje się, że wówczas okrąg opisany na punktach 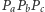 zawiera spodki wysokości trójkąta
zawiera spodki wysokości trójkąta  - jest to słynny okrąg dziewięciu punktów. W tej sytuacji punkt
- jest to słynny okrąg dziewięciu punktów. W tej sytuacji punkt 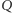 ze stwierdzenia 1 staje się ortocentrum trójkąta
ze stwierdzenia 1 staje się ortocentrum trójkąta 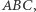 a punktem
a punktem 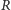 z naszego twierdzenia jest, rzecz jasna, środek ciężkości trójkąta
z naszego twierdzenia jest, rzecz jasna, środek ciężkości trójkąta 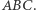 Pokazaliśmy więc współliniowość środka okręgu opisanego, środka okręgu 9 punktów, ortocentrum i środka ciężkości - geometryczni smakosze z łatwością rozpoznają w tym prostą Eulera.
Pokazaliśmy więc współliniowość środka okręgu opisanego, środka okręgu 9 punktów, ortocentrum i środka ciężkości - geometryczni smakosze z łatwością rozpoznają w tym prostą Eulera.
Warto zaznaczyć, że prosta Eulera nie jest określona dla trójkąta równobocznego, a nasza oś 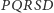 istnieje, o ile tylko nie przyjmiemy, że
istnieje, o ile tylko nie przyjmiemy, że  to środek okręgu wpisanego. Zachęcamy Czytelnika do poszukiwań innych ciekawych prostych, których istnienie gwarantowane jest przez podane przez nas twierdzenie!
to środek okręgu wpisanego. Zachęcamy Czytelnika do poszukiwań innych ciekawych prostych, których istnienie gwarantowane jest przez podane przez nas twierdzenie!