Drobiazgi
Polecamy bardzo trudne zadanie
O zadaniu 16. z książki 100 zadań Steinhausa.
W znakomitych 100 zadaniach Steinhausa jako zadanie szesnaste znajdujemy:
Zadanie. Mamy dowolny trójkąt. Możemy go oczywiście przeciąć linią prostą tak, żeby przepołowić jego obwód. Możemy nawet z góry przypisać kierunek linii przecinającej. Gdy zrobimy to dwa razy, używając dwu różnych kierunków, linie proste przetną się w pewnym punkcie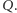 
Wtedy przez punkt 
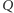wiodą dwie linie proste przepoławiające obwód. Czy istnieje punkt, przez który wiodą trzy takie linie? Jeśli tak, to jak go znaleźć?
Odpowiedź jest zaskakująca: przez każdy punkt, przez który przechodzą dwie proste połowiące obwód, przechodzi też trzecia mająca tę własność.
A trudność w znalezieniu odpowiedzi leży w tym, że trzeba jakoś scharakteryzować możliwe położenia punktu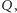 
o którym jest mowa w zadaniu - okazuje się, że są to punkty trójkąta krzywoliniowego zawierającego w brzegu łuki trzech paraboli stycznych do dwóch spośród prostych zawierających boki trójkąta.
Ciekawe jest to, że wynik jest mocniejszy: przez każdy punkt trójkąta przechodzi albo dokładnie jedna, albo dokładnie trzy proste połowiące obwód; to samo dotyczy czworokąta niebędącego równoległobokiem (a jak jest dla niego?).
Nie wątpię, że Czytelnik Ambitny podejmie to wyzwanie.