Przeskocz do treści

Delta mi!

Drobiazgi

Krótki dowód twierdzenia Routha

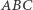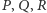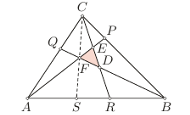
Niech $|ABC$ będzie dowolnym trójkątem, a $P | ,Q,$ punktami leżącymi odpowiednio na bokach 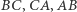$BC,$ (Rys. 1). Przyjmijmy, że 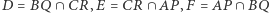$=BQ∩CDR, E = CR$ oraz niech

BP- = p, CQ-- = q, AR- = r. P C QA RB

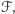Oznaczając przez $[ℱ]$ pole figury $|ℱ,$ mamy następujący wzór

2 EF] [D-----= ------------(pqr-−1)------------, [ABC] (1 +p + pq)(1 +q + qr)(1+ r+ rp)

znany pod nazwą twierdzenia Routha.

Dowody tego wzoru, które można znaleźć w dostępnej literaturze, używają na ogół rachunku wektorowego lub geometrii analitycznej. Podamy tutaj krótki geometryczny dowód tego twierdzenia.

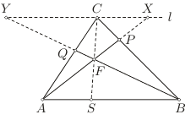
obrazek — Rys. 1

obrazek — Rys. 2

Poprowadźmy przez punkt 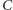$|C$ prostą 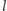$l |$ równoległą do prostej 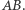$|AB.$ Niech ponadto 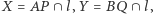$=AP∩l,Y=BQ∩l, |X$ a także 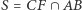$|S = CF$ (Rys. 2). Korzystając z twierdzenia Talesa, uzyskujemy

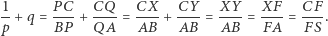YF 1- P-C CQ-- CX-- CY-- X--- X--- CF- p +q = BP + QA= AB+ AB= AB= FA= FS .

(*)

Wobec tego

[ABC]-- CS- CF- 1- 1+-p-+-pq [ABF]= FS = 1+ FS = 1+ p +q = p .

Analogicznie otrzymujemy

[ABC]-- 1+-q-+qr- [ABC]-- 1-+r-+-rp ] [BCD = q oraz [CAE]= r .

Stąd ostatecznie obliczamy:

$pict$

co kończy dowód.

Uwaga. Udowodniona tożsamość 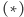$(∗ )$ nosi nazwę twierdzenia van Aubela.