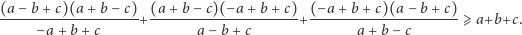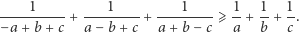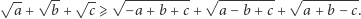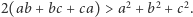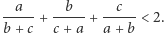Przeskocz do treści

Delta mi!

Deltoid

Boki trójkąta

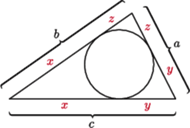
obrazek

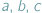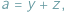
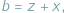
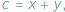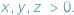Jeśli w nierówności, którą chcemy uzasadnić, występują długości boków $|a;b;c$ pewnego trójkąta, często przydaje się podstawienie Raviego: $|a = y + z;$ $b = z + x;$ $c = x + y ;$ gdzie $x;y ;z > 0:$ Takie liczby 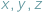$|x;y;z$ zawsze istnieją, są to bowiem długości odcinków stycznych do okręgu wpisanego w trójkąt.

Nierówność średnich dla liczb 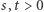$s,t > 0$ :

√ ------- s2 +-t2⩾ s-+t ⩾ √ st⩾---2----. 2 2 1/s+ 1/t

Średnie te to kolejno: kwadratowa 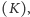$(K),$ arytmetyczna 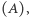$(A), |$ geometryczna 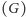$) (G |$ i harmoniczna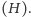 $(H).$

Zadanie 1.

(a-−b-+-c)(a-+b-−-c) (a+-b-−-c)(−a-+b-+-c)- (−a-+b-+-c)(a-−b-+-c)- − a+ b + c + a − b+ c + a + b− c ⩾a+b+c.

Zadanie 2.

----1-----+ ---1----+ ----1--- ⩾ 1-+ 1-+ 1. −a + b+ c a− b + c a + b− c a b c

Zadanie 3.

√ -- √-- √ -- √ ---------- √-------- √ -------- a + b + c⩾ −a + b +c + a − b +c + a+ b −c.

Zadanie 4. $|abc ⩾ (−a +b + c)(a− b + c)(a+ b − c).$

Zadanie 5. $|2(ab +bc + ca) > a2 + b2 + c2.$

Zadanie 6. $--a-- --b-- --c-- |b +c + c +a + a + b < 2.$

Zadanie 7. Wykaż, że jeśli $x,y,z > 0,$ to $|-x---+ -y---+ --z--⩾ 3. y+ z z+ x x +y 2$

Autorem nierówności 4 jest Alessandro Padoa, natomiast nierówność 7 to nierówność Alfreda Nesbitta.

Cały artykuł dostępny jest w wersji do druku [application/pdf]: (67 KB)