O stopniu równoważności wielokątów

wikipedia
Alfred Tarski (1901-1983)
W artykule tym pragnę omówić pewne pojęcia, należące całkowicie do zakresu geometrii elementarnej, a dotąd niemal wcale nie zbadane. Jak wiadomo, dwa wielokąty  i
i  nazywamy równoważnymi, wyrażając to wzorem:
nazywamy równoważnymi, wyrażając to wzorem: 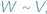 jezeli dają się one podzielić na jednakową ilość wielokątów odpowiednio przystających...
jezeli dają się one podzielić na jednakową ilość wielokątów odpowiednio przystających...
Ten podział wielokątów równoważnych na części przystające nie jest jednoznaczny: dwa wielokąty równoważne dają się podzielić na części przystające w sposób rozmaity zarówno pod względem liczby, jak i kształtu tych części.
Wyjaśnimy to na przykładzie.
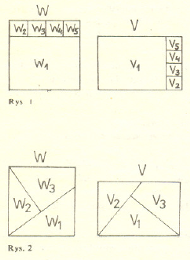
Zarówno Rys. 1, jak i Rys. 2, wykazują, że kwadrat o boku a oraz prostokąt o bokach 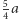 i
i 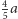 są sobie równoważne, ale ich podziały na obu rysunkach są zgolą rożne. W związku z tem spostrzeżeniem nasuwa się w sposób naturalny pytanie: na jaka najmniejszą liczbę części odpowiednio przystających można podzielić dwa dane wielokąty równoważne? Zagadnienia tego właśnie typu pragniemy poruszyć w Parametrze. W tym celu przyjmiemy następująca definicje: Stopniem równoważności dwóch wielokątów równoważnych
są sobie równoważne, ale ich podziały na obu rysunkach są zgolą rożne. W związku z tem spostrzeżeniem nasuwa się w sposób naturalny pytanie: na jaka najmniejszą liczbę części odpowiednio przystających można podzielić dwa dane wielokąty równoważne? Zagadnienia tego właśnie typu pragniemy poruszyć w Parametrze. W tym celu przyjmiemy następująca definicje: Stopniem równoważności dwóch wielokątów równoważnych  i
i  nazywamy najmniejszą liczbę naturalną
nazywamy najmniejszą liczbę naturalną 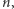 czyniąca zadość warunkowi: każdy z wielokątów
czyniąca zadość warunkowi: każdy z wielokątów  i
i 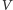 daje się podzielić na
daje się podzielić na  wielokątów w ten sposób, że wielokąty, otrzymane z podziału
wielokątów w ten sposób, że wielokąty, otrzymane z podziału 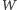 odpowiednio przystają do wielokątów, otrzymanych z podziału
odpowiednio przystają do wielokątów, otrzymanych z podziału 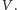 - Stopień równoważności wielokątów
- Stopień równoważności wielokątów 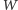 i
i 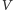 będziemy oznaczali symbolem:
będziemy oznaczali symbolem: 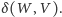
Należy tu uczynić pewną uwagę. Wyrazowi wielokąt dogodnie jest nadać w niniejszych rozważaniach znaczenie szersze niż to, które jest stosowane w początkach nauczania geometrii elementarnej. Mianowicie, wielokątem w znaczeniu szerszym nazywamy tu figurę płaską, która jest zestawieniem skończonej liczby wielokątów w pospolitem znaczeniu tego wyrazu. Tak np. wielokątem w znaczeniu szerszym jest figura, złożona z prostokątów 2 i 4 na Rys. 1, lub też figura, złożona z obu tych prostokątów i ponadto czworokąta 3 na Rys. 2. Zaznaczamy mimochodem, że rozszerzenie pojęcia wielokąta jest niezmiernie użyteczne w całej teorii równoważności wielokątów: bez tego rozszerzenia wiele rozumowań z tej teorji, spotykanych w podręcznikach elementarnych, grzeszy brakiem ścisłości.

W zastosowaniu do wielokątów w znaczeniu szerszym nastręcza pewna trudność poprawne zdefiniowanie pojęcia przystawania. Ograniczymy się tu do następującego wyjaśnienia poglądowego: dwa wielokąty w znaczeniu szerszym - podobnie jak i wszelkie figury geometryczne - przystają, jeżeli jeden z nich można "nałożyć" na drugi (nie zmieniając wzajemnego położenia składowych części żadnego z nich) w ten sposób, aby się "pokryły". Tak np. wielokąt, przedstawiony na Rys. 3, nie przystaje do wielokąta, przedstawionego na Rys. 4, ale jest z nim równoważny.
- Cały artykuł dostępny jest w wersji do druku [application/pdf]: (851 KB)