Deltoid
Mały wybór? I dobrze!
Izometrią nazywamy przekształcenie, które nie zmienia odległości między punktami. Obrazy trzech niewspółliniowych punktów jednoznacznie ją wyznaczają. Twierdzenie Chaslesa głosi, że każda izometria płaszczyzny jest przesunięciem, obrotem lub symetrią z poślizgiem.
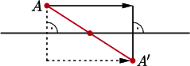
Rys. 1 Gdy wektor przesunięcia jest zerowy, uzyskujemy symetrię osiową
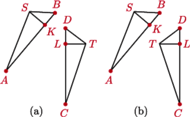
Rys. 2 Trójkąty 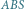 i
i 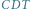 są (a) przeciwnie i (b) zgodnie zorientowane
są (a) przeciwnie i (b) zgodnie zorientowane
Symetria z poślizgiem to złożenie (w dowolnej kolejności) symetrii osiowej z przesunięciem o wektor równoległy do osi (Rys. 1). Przekształcenie to zmienia orientację (Rys. 2). Z kolei przesunięcie i obrót nie zmieniają orientacji, a szczególnym przypadkiem każdego z nich jest identyczność.
Uwaga *. Przy symetrii z poślizgiem środek odcinka łączącego punkt i jego obraz leży na osi symetrii (Rys. 1).
Uwaga **. Niech punkty 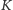 i
i 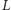 należą odpowiednio do odcinków
należą odpowiednio do odcinków 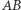 i
i 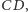 przy czym
przy czym 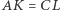 (Rys. 2). Zbudujmy na odcinkach
(Rys. 2). Zbudujmy na odcinkach 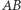 i
i 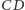 przystające trójkąty
przystające trójkąty 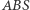 i
i 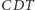 o spodkach wysokości odpowiednio
o spodkach wysokości odpowiednio 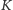 i
i 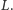 Można zrobić to dwojako: tak, by trójkąty te były przeciwnie lub zgodnie zorientowane. W każdym z przypadków istnieje dokładnie jedna izometria przeprowadzająca jeden na drugi. W pierwszym przypadku jest ona symetrią z poślizgiem. W drugim jest to przesunięcie, jeśli
Można zrobić to dwojako: tak, by trójkąty te były przeciwnie lub zgodnie zorientowane. W każdym z przypadków istnieje dokładnie jedna izometria przeprowadzająca jeden na drugi. W pierwszym przypadku jest ona symetrią z poślizgiem. W drugim jest to przesunięcie, jeśli 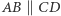 lub obrót, jeśli
lub obrót, jeśli 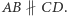
Więcej o prostej Simsona w deltoidzie z numeru 10/2015.
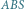 i
i 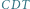 są (a) przeciwnie i (b) zgodnie zorientowane
są (a) przeciwnie i (b) zgodnie zorientowane