Siedmiokąta foremnego nie można skonstruować cyrklem i linijką
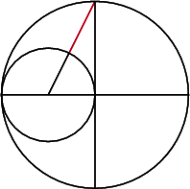
...a pięciokąt foremny można. Obok pokazana jest konstrukcja dziesięciokąta foremnego - kolorowy odcinek ma długość boku dziesięciokąta foremnego wpisanego w większy okrąg, a więc biorąc co drugi z wierzchołków takiego dziesięciokąta, otrzymamy pięciokąt foremny. Konstrukcja jest - jak widać - bardzo prosta. Ma tylko tę wadę, że nie wskazuje, jak konstruować inne wielokąty foremne.
Dziewiętnastoletni Carl Gauss (w 1796 roku) skonstruował pięciokąt w zupełnie inny sposób. Sposób ten ma z kolei tę wadę, że używa (prawda, że bardzo oszczędnie, ale jednak) liczb zespolonych. Natomiast ma tę zaletę, że stosując go, można skonstruować wszystkie  -kąty foremne, dla których taka konstrukcja może istnieć i dla których
-kąty foremne, dla których taka konstrukcja może istnieć i dla których 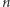 jest liczbą pierwszą. W konsekwencji, posługując się tą konstrukcją, można skonstruować wszystkie wielokąty foremne, dla których konstrukcja cyrklem i linijką jest możliwa. Już Euklides udowodnił bowiem, że jeśli umiemy skonstruować
jest liczbą pierwszą. W konsekwencji, posługując się tą konstrukcją, można skonstruować wszystkie wielokąty foremne, dla których konstrukcja cyrklem i linijką jest możliwa. Już Euklides udowodnił bowiem, że jeśli umiemy skonstruować 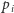 -kąt foremny dla (różnych) liczb pierwszych
-kąt foremny dla (różnych) liczb pierwszych 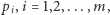 to umiemy skonstruować
to umiemy skonstruować  -kąt foremny dla
-kąt foremny dla

gdzie 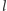 jest dowolną liczbą naturalną.
jest dowolną liczbą naturalną.
Konstrukcje Gaussa stosują się do tzw. liczb pierwszych Fermata, czyli liczb pierwszych postaci 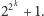 Czterdzieści lat po konstrukcji Gaussa Pierre Wanzel wykazał, że dla innych liczb pierwszych konstrukcja nie jest możliwa. Nie znaczy to, że wiemy w tej sprawie już wszystko, bo znamy tylko pięć liczb pierwszych Fermata: 3, 5, 17, 257, 65537, i nie wiemy, czy istnieją jeszcze inne.
Czterdzieści lat po konstrukcji Gaussa Pierre Wanzel wykazał, że dla innych liczb pierwszych konstrukcja nie jest możliwa. Nie znaczy to, że wiemy w tej sprawie już wszystko, bo znamy tylko pięć liczb pierwszych Fermata: 3, 5, 17, 257, 65537, i nie wiemy, czy istnieją jeszcze inne.
Użycie liczb zespolonych w konstrukcji Gaussa jest oszczędne: pojawiają się jedynie pierwiastki z jedności. Pierwiastek  -tego stopnia z jedności to taka liczba
-tego stopnia z jedności to taka liczba  (w tym przypadku zespolona), która podniesiona do
(w tym przypadku zespolona), która podniesiona do  -tej potęgi daje 1. Oznacza to (jak łatwo zauważyć, posługując się definicją mnożenia liczb zespolonych), że
-tej potęgi daje 1. Oznacza to (jak łatwo zauważyć, posługując się definicją mnożenia liczb zespolonych), że  obrócone o
obrócone o 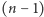 -krotność kąta
-krotność kąta 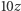 wokół 0 staje się jedynką.
wokół 0 staje się jedynką.
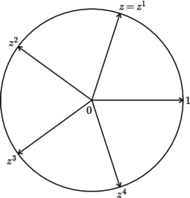
Rys. 1
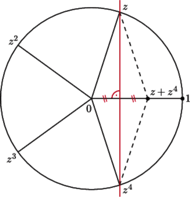
Zapewne nie od razu zobaczymy, że wszystkie pięć punktów na okręgu na rysunku 1 to pierwiastki piątego stopnia z jedności. Zauważmy jednak, że nie przez pomyłkę ponumerowane zostały "u góry" - faktycznie są to potęgi 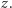
Rys. 2
Natomiast od razu widzimy, że są to wierzchołki pięciokąta foremnego. Korzyść z tego spostrzeżenia jest taka, że suma wektorów 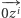 jest równa zeru - układ jest zrównoważony, żaden z wektorów nie ma przewagi. Zatem
jest równa zeru - układ jest zrównoważony, żaden z wektorów nie ma przewagi. Zatem
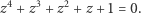 |
(*) |
A teraz sztuczka (a jakże, Gaussa): ponieważ 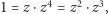 więc równanie (*) możemy zapisać jako
więc równanie (*) możemy zapisać jako

Jeśli więc oznaczymy 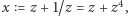 to otrzymamy równanie
to otrzymamy równanie

Odcinek o długości 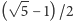 łatwo skonstruować cyrklem i linijką, a rysunek 2 pokazuje, jak zastosować to do znalezienia położenia
łatwo skonstruować cyrklem i linijką, a rysunek 2 pokazuje, jak zastosować to do znalezienia położenia  (i
(i 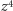 ) na okręgu jednostkowym, czyli jak skonstruować pięciokąt foremny. Ten sposób rozumowania daje się użyć w przypadku, gdy 5 zastąpimy dowolną z liczb pierwszych Fermata (oczywiście, im taka liczba będzie większa, tym rozumowanie dłuższe).
) na okręgu jednostkowym, czyli jak skonstruować pięciokąt foremny. Ten sposób rozumowania daje się użyć w przypadku, gdy 5 zastąpimy dowolną z liczb pierwszych Fermata (oczywiście, im taka liczba będzie większa, tym rozumowanie dłuższe).
Dlaczego jednak nie da się go użyć np. do konstrukcji siedmiokąta foremnego? Spróbujmy.
Równanie 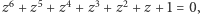 gdzie
gdzie  to pierwiastek siódmego stopnia z jedności, daje się zastąpić przez
to pierwiastek siódmego stopnia z jedności, daje się zastąpić przez

Ponieważ

oraz

więc

czyli po podstawieniu 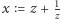 mamy
mamy
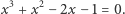 |
(**) |
Równanie to, jak każde równanie stopnia nieparzystego, ma pierwiastek rzeczywisty, ale nie jest jasne, czy warto go szukać, bo interesują nas tylko takie wartości, które można uzyskać z 1 przez stosowanie dodawania, odejmowania, mnożenia i dzielenia oraz wyciągania pierwiastków kwadratowych, bo tylko takie działania dają się zrealizować za pomocą cyrkla i linijki.
I faktycznie nie warto - wspomniany już Wanzel udowodnił, że:
Twierdzenie. Jeśli długość odcinka da się opisać równaniem stopnia trzeciego o współczynnikach wymiernych, to odcinek taki da się skonstruować z odcinka o długości 1 wtedy i tylko wtedy, gdy równanie to ma pierwiastek wymierny.
Myśl Wanzela możemy sobie przybliżyć, rozpatrując na początek sytuację, gdy długość rozpatrywanego odcinka jest liczbą postaci 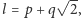 a równanie, które ją opisuje, to
a równanie, które ją opisuje, to 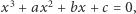 gdzie liczby
gdzie liczby 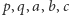 są wymierne (symbolicznie: należą do
są wymierne (symbolicznie: należą do 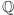 ). Podstawiając
). Podstawiając 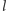 do równania, otrzymujemy
do równania, otrzymujemy

z czego wynika, że 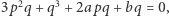 bo są to współczynniki przy
bo są to współczynniki przy 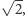 a pozostałe liczby, łącznie z zerem, są wymierne. Ale skoro tak, to mamy również
a pozostałe liczby, łącznie z zerem, są wymierne. Ale skoro tak, to mamy również

co oznacza, że również 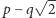 jest pierwiastkiem rozpatrywanego równania.
jest pierwiastkiem rozpatrywanego równania.
Teraz przypomnijmy sobie wzory Viète'a:  jest sumą wszystkich pierwiastków równania. Oznaczając pozostały pierwiastek równania przez
jest sumą wszystkich pierwiastków równania. Oznaczając pozostały pierwiastek równania przez  (bo dwa już mamy), otrzymujemy
(bo dwa już mamy), otrzymujemy 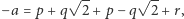 a więc
a więc 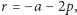 zatem jest liczbą wymierną.
zatem jest liczbą wymierną.
Uogólnienie I. Pierwiastek nie musi być z dwóch - może być z dowolnej liczby wymiernej 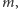 o ile tylko
o ile tylko 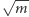 nie jest liczbą wymierną. Dowód przebiegnie bez zmian.
nie jest liczbą wymierną. Dowód przebiegnie bez zmian.
Uogólnienie II. Na ogół trzeba więcej razy wyciągać pierwiastek kwadratowy - robimy to po kolei (używając kolejno w konstrukcji cyrkla). Jeśli więc stwierdzimy, że dla liczb 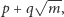
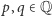 musi istnieć pierwiastek wymierny, nazwijmy te liczby
musi istnieć pierwiastek wymierny, nazwijmy te liczby 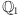 i rozważmy nasze równanie, przypuszczając, że ma pierwiastek wśród liczb postaci
i rozważmy nasze równanie, przypuszczając, że ma pierwiastek wśród liczb postaci 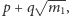 gdzie
gdzie 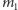 jest, a
jest, a 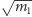 nie jest liczbą z
nie jest liczbą z 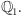 Wynik będzie taki sam jak poprzednio: otrzymamy najpierw, że istnieje pierwiastek w
Wynik będzie taki sam jak poprzednio: otrzymamy najpierw, że istnieje pierwiastek w 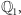 a (na mocy poprzedniego), że istnieje pierwiastek w
a (na mocy poprzedniego), że istnieje pierwiastek w 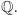
Operację tę będziemy powtarzali tyle razy, ile razy będziemy potrzebowali (rysując jakiś okrąg) wyciągać pierwiastki z dotychczas uzyskanych liczb.
Skoro tak, to siedmiokąta foremnego cyrklem i linijką skonstruować się nie da, bo równanie (**) pierwiastka wymiernego nie ma (mógłby on być równy tylko 1 lub 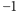 - prawda?).
- prawda?).
A co dalej? Polecam samodzielnie obmyślić dalszą drogę do twierdzenia Wanzela o niekonstruowalności innych wielokątów foremnych, poza tymi, które można skonstruować metodą Gaussa.
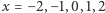 przyjmuje odpowiednio wartości -1, 1, -1, -1, 7, czyli zmienia znak między -2 i -1, między -1 i 0 oraz między 1 i 2.
przyjmuje odpowiednio wartości -1, 1, -1, -1, 7, czyli zmienia znak między -2 i -1, między -1 i 0 oraz między 1 i 2.