Zabawy w kącie
W każdym zjawisku przyrody można dostrzec dążenie do osiągnięcia jakiegoś maksimum lub minimum. Umiejętność wyznaczania wartości ekstremalnych nie powinna więc być niczym niezwykłym...
Oto zadanie z niespodzianką, które proponuję rozwiązać samodzielnie (wrócimy do niego na końcu artykułu):
Tymczasem rozważymy kilka innych ciekawych problemów.
Rozwiązanie zadania 1

Rys. 1
Rozpoczniemy od wykazania, że istnieje najkrótszy odcinek realizujący warunki zadania. Niech 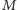 będzie danym punktem we wnętrzu kąta o wierzchołku
będzie danym punktem we wnętrzu kąta o wierzchołku 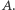 Odcinek, którego końce ślizgają się po ramionach kąta od położenia
Odcinek, którego końce ślizgają się po ramionach kąta od położenia 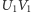 przez
przez 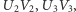 itd. do położenia
itd. do położenia 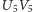 (Rys. 1) i przechodzący przez punkt
(Rys. 1) i przechodzący przez punkt 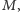 zmienia swoją długość w sposób ciągły. Ponieważ długość ta najpierw maleje, a potem wzrasta, więc wśród rozpatrywanych odcinków istnieje taki odcinek
zmienia swoją długość w sposób ciągły. Ponieważ długość ta najpierw maleje, a potem wzrasta, więc wśród rozpatrywanych odcinków istnieje taki odcinek 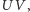 którego długość jest najmniejsza.
którego długość jest najmniejsza.
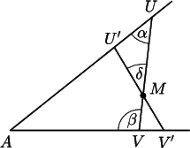
Rys. 2
Spróbujmy ten odcinek scharakteryzować. Niech 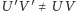 będzie innym odcinkiem zawierającym punkt
będzie innym odcinkiem zawierającym punkt 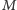 i łączącym ramiona kąta. Niech
i łączącym ramiona kąta. Niech 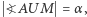
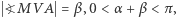 a mniejszy z kątów o wierzchołku
a mniejszy z kątów o wierzchołku 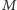 (między odcinkami
(między odcinkami 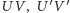 ) ma miarę
) ma miarę 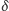 (Rys. 2). Dla małych kątów
(Rys. 2). Dla małych kątów 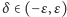 rozważmy funkcję
rozważmy funkcję

Z twierdzenia sinusów, zastosowanego do trójkątów 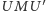 i
i 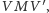 mamy
mamy

więc

Funkcja ta jest różniczkowalna, osiąga minimum dla 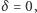 więc zgodnie z twierdzeniem Fermata spełnia warunek
więc zgodnie z twierdzeniem Fermata spełnia warunek 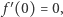 który po obliczeniu pochodnej i niezbyt skomplikowanych przekształceniach trygonometrycznych jest równoważny warunkowi
który po obliczeniu pochodnej i niezbyt skomplikowanych przekształceniach trygonometrycznych jest równoważny warunkowi

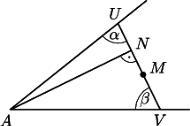
Rys. 3
Jaki jest sens geometryczny tego warunku? Niech 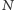 będzie rzutem (prostopadłym) wierzchołka
będzie rzutem (prostopadłym) wierzchołka 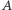 na odcinek
na odcinek 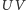 (Rys. 3). Wyznaczając
(Rys. 3). Wyznaczając 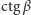 i
i 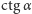 z trójkątów prostokątnych
z trójkątów prostokątnych 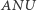 i
i 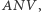 łatwo stwierdzamy, że
łatwo stwierdzamy, że 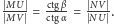 Oznacza to, że
Oznacza to, że 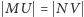 i
i 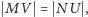 czyli punkt
czyli punkt 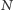 jest symetryczny do punktu
jest symetryczny do punktu 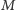 względem środka odcinka
względem środka odcinka 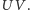
Rys. 4
Niespodzianką (trudnością) w tym zadaniu jest to, że - poza szczególnymi przypadkami - odcinka 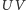 nie można skonstruować za pomocą cyrkla i linijki. Dlaczego tak jest? Niech kąt przy wierzchołku
nie można skonstruować za pomocą cyrkla i linijki. Dlaczego tak jest? Niech kąt przy wierzchołku 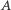 będzie prosty. Wtedy, przy oznaczeniach takich jak na rysunku 4, jeśli
będzie prosty. Wtedy, przy oznaczeniach takich jak na rysunku 4, jeśli 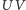 jest najkrótszym odcinkiem łączącym ramiona kąta i przechodzącym przez punkt
jest najkrótszym odcinkiem łączącym ramiona kąta i przechodzącym przez punkt 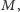 to
to

Z twierdzenia Talesa 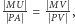 więc
więc 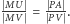 Ponieważ
Ponieważ 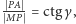
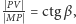 więc
więc

gdzie 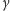 jest miarą kąta
jest miarą kąta 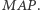 W konsekwencji
W konsekwencji 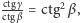 więc
więc 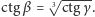 Gdyby istniała konstrukcja najkrótszego odcinka
Gdyby istniała konstrukcja najkrótszego odcinka 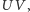 to, biorąc
to, biorąc 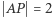 i
i 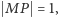 otrzymamy odcinek
otrzymamy odcinek 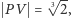 który umożliwia wykonanie zadania podwojenia sześcianu jednostkowego. Wystarczy teraz wiedzieć (!), że jest to niemożliwe do zrealizowania za pomocą cyrkla i linijki (patrz np. M. Bryński, L. Włodarski, Konstrukcje geometryczne, Biblioteczka Delty 1, WSiP, Warszawa 1979).
który umożliwia wykonanie zadania podwojenia sześcianu jednostkowego. Wystarczy teraz wiedzieć (!), że jest to niemożliwe do zrealizowania za pomocą cyrkla i linijki (patrz np. M. Bryński, L. Włodarski, Konstrukcje geometryczne, Biblioteczka Delty 1, WSiP, Warszawa 1979).
Puentą niech będą słowa Adama Mickiewicza
"Na co będą potrzebne, pytało pacholę - Trójkąty, czworoboki, koła, parabole?" "Że potrzebne - rzekł mędrzec - musisz teraz wierzyć; Na co potrzebne, zgadniesz, gdy zaczniesz świat mierzyć."
PRAKTYKA