Prosto w środek
Przeciętny uczeń rozpoczyna podróż po fascynującym świecie geometrycznych konstrukcji uzbrojony w linijkę i kątomierz. Kiedy już nauczyciel uzna swojego podopiecznego za wystarczająco odpowiedzialnego, by nie rysował szkolnych ławek (jakże często zbyt naiwne założenie), uczeń dostaje do ręki kolejne narzędzie walki z czystą kartką papieru, jakim jest cyrkiel...

Rys. 1
Wraz z nastaniem ery cyrklowej uczeń jest zdolny rysować w zeszycie całe mnóstwo okręgów o zadanym środku, czasem nawet mając w tym jakiś wyższy konstrukcyjny cel. Przykładem tego ostatniego mogłaby być operacja w pewnym sensie odwrotna - skonstruowanie środka okręgu, gdy mamy zadany jedynie sam okrąg. Chwila zastanowienia pozwala stwierdzić, że gdy jesteśmy wyposażeni w cyrkiel i linijkę, zadanie to nie stanowi większego wyzwania; wystarczy narysować dwie nierównoległe cięciwy okręgu, a następnie ich symetralne, których przecięcie wyznaczy nam, oczywiście, szukany środek (Rys. 1).
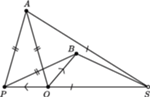
Rys. 2
Schody pojawiają się, jeśli zazdrosny o nasze sukcesy kolega z ławki podprowadzi nam linijkę. Skarżenie nauczycielowi jest poniżej naszej godności, podobnie rozwiązanie tej kwestii po lekcjach na szkolnym podwórku, dlatego zaciskamy zęby i próbujemy wyznaczyć środek okręgu przy użyciu samego cyrkla. W rozwiązaniu przydatna okazuje się następująca konfiguracja geometryczna (Rys. 2): jeśli 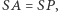 punkt
punkt 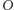 leży na odcinku
leży na odcinku 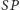 i spełnia
i spełnia 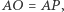 natomiast dla punktu
natomiast dla punktu 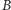 zachodzą równości
zachodzą równości 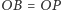 oraz
oraz 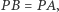 to wówczas
to wówczas 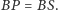 Istotnie, zauważmy, że przy przedstawionych założeniach trójkąty
Istotnie, zauważmy, że przy przedstawionych założeniach trójkąty 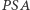 i
i 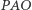 są podobne (jako równoramienne trójkąty o tym samym kącie przy podstawie), dlatego korzystając z założonych równości, otrzymujemy
są podobne (jako równoramienne trójkąty o tym samym kącie przy podstawie), dlatego korzystając z założonych równości, otrzymujemy


Rys. 3
Rys. 4
Z powyższego i z zasady "bok-kąt-bok" wnioskujemy podobieństwo trójkątów 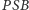 i
i 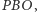 a skoro ten ostatni jest równoramienny, to musi zachodzić
a skoro ten ostatni jest równoramienny, to musi zachodzić 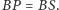 Przedstawioną obserwację można łatwo wykorzystać do dowodu poprawności niniejszej konstrukcji środka zadanego okręgu
Przedstawioną obserwację można łatwo wykorzystać do dowodu poprawności niniejszej konstrukcji środka zadanego okręgu  przy użyciu samego cyrkla. Dla skrócenia zapisu niech oznaczenie okręgu przez
przy użyciu samego cyrkla. Dla skrócenia zapisu niech oznaczenie okręgu przez 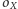 niesie ze sobą informację, że
niesie ze sobą informację, że 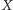 jest środkiem tego okręgu. Należy narysować kolejno:
jest środkiem tego okręgu. Należy narysować kolejno:
- wystarczająco duży okrąg
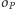 (wystarczająco duży, czyli taki, dla którego
(wystarczająco duży, czyli taki, dla którego 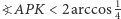 ; można nietrudno sprawdzić, że w przeciwnym przypadku nie uzyskamy punktów
; można nietrudno sprawdzić, że w przeciwnym przypadku nie uzyskamy punktów 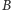 i
i 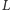 z kroku 3), gdzie
z kroku 3), gdzie 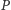 należy do okręgu
należy do okręgu  ; niech
; niech 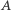 i
i 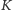 będą punktami przecięcia
będą punktami przecięcia  z
z 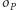 (Rys. 3),
(Rys. 3), - okręgi
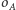 i
i 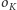 o promieniu
o promieniu 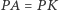 ; niech
; niech 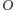 będzie różnym od
będzie różnym od 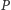 przecięciem tych okręgów (Rys. 3),
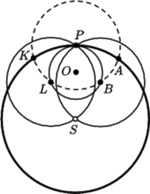
przecięciem tych okręgów (Rys. 3), - okrąg
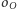 o promieniu
o promieniu 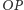 i niech
i niech 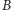 i
i 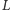 będą przecięciami nowego okręgu z
będą przecięciami nowego okręgu z 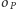 (Rys. 4),
(Rys. 4), - punkt
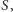 będący przecięciem (różnym od
będący przecięciem (różnym od 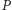 ) okręgów
) okręgów 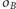 i
i 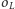 o promieniu
o promieniu 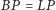 (Rys. 4).
(Rys. 4).
Tak skonstruowany punkt 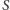 stanowi szukany środek okręgu
stanowi szukany środek okręgu 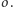 Istotnie, jeśli nieufnie oznaczymy ów środek przez
Istotnie, jeśli nieufnie oznaczymy ów środek przez 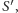 to w trzecim kroku konstrukcji punkty
to w trzecim kroku konstrukcji punkty 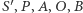 tworzą konfigurację przedstawioną na rysunku 2 i w tej sytuacji okrąg
tworzą konfigurację przedstawioną na rysunku 2 i w tej sytuacji okrąg 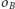 z punktu 4 przechodzi przez
z punktu 4 przechodzi przez 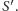 Analogicznie, przez
Analogicznie, przez 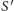 przechodzi również
przechodzi również 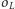 i dlatego
i dlatego 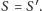
Udało nam się utrzeć nosa niedobremu koledze i zachęceni tym dokonaniem, postanowiliśmy dokonać tej samej sztuki wyłącznie przy użyciu odzyskanej w glorii linijki. Początkowy entuzjazm prędko przeradza się jednak w niepokój, a wkrótce zaczynają się pojawiać oznaki paniki. Pomimo prężenia intelektualnych muskułów i dziesiątek prób dokonanych na kilkunastu wyrzuconych ostatecznie do kosza kartkach środek okręgu  skutecznie unika namierzenia przez nasz nowy oręż. Po kolejnym nieudanym podejściu w naszej głowie pojawia się iskierka nadziei - może wszystkie niepowodzenia nie są kwestią naszej umysłowej niedyspozycji, a tego, że po prostu się nie da? Jak jednak mogłoby wyglądać uzasadnienie tego, że czegoś nie da się skonstruować przy użyciu samej linijki? Po chwili zastanowienia jedyne, co przychodzi nam do głowy, to pokazanie, że nawet jeśli pewien konstrukcyjny przepis sprawdzi się na jednym okręgu, polegnie na innym. Gdzie jednak należy szukać tego drugiego okręgu? Okazuje się, że na innej kartce!
skutecznie unika namierzenia przez nasz nowy oręż. Po kolejnym nieudanym podejściu w naszej głowie pojawia się iskierka nadziei - może wszystkie niepowodzenia nie są kwestią naszej umysłowej niedyspozycji, a tego, że po prostu się nie da? Jak jednak mogłoby wyglądać uzasadnienie tego, że czegoś nie da się skonstruować przy użyciu samej linijki? Po chwili zastanowienia jedyne, co przychodzi nam do głowy, to pokazanie, że nawet jeśli pewien konstrukcyjny przepis sprawdzi się na jednym okręgu, polegnie na innym. Gdzie jednak należy szukać tego drugiego okręgu? Okazuje się, że na innej kartce!
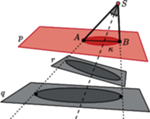
Rys. 5
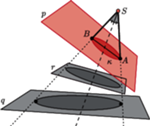
Rys. 6
Zamalujmy na przezroczystej kartce 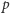 koło
koło 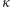 ograniczone okręgiem
ograniczone okręgiem 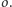 Nad kartką
Nad kartką 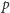 umieśćmy punktowe źródło światła
umieśćmy punktowe źródło światła 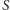 w taki sposób, by na pewno nie znajdowało się ono bezpośrednio nad środkiem okręgu
w taki sposób, by na pewno nie znajdowało się ono bezpośrednio nad środkiem okręgu  Pod kartkę
Pod kartkę 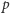 podłóżmy równoległą do niej kartkę
podłóżmy równoległą do niej kartkę 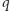 - nietrudno przekonać się, że koło
- nietrudno przekonać się, że koło  będzie rzucało na
będzie rzucało na 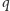 cień w kształcie koła. Wyobraźmy sobie teraz, że ze środka
cień w kształcie koła. Wyobraźmy sobie teraz, że ze środka  wystaje maszt i niech
wystaje maszt i niech 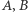 będą punktami przecięcia okręgu
będą punktami przecięcia okręgu  z przedłużeniem cienia masztu. Między kartki
z przedłużeniem cienia masztu. Między kartki 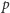 i
i 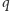 wstawmy teraz na chwilę kartkę
wstawmy teraz na chwilę kartkę 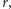 prostopadłą do dwusiecznej kąta
prostopadłą do dwusiecznej kąta 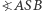 - wówczas
- wówczas  rzuca na
rzuca na  cień w kształcie elipsy, której środek symetrii wyznaczany jest przez przecięcie
cień w kształcie elipsy, której środek symetrii wyznaczany jest przez przecięcie  ze wspomnianą dwusieczną (Rys. 5). W tej sytuacji, jeśli przymocujemy
ze wspomnianą dwusieczną (Rys. 5). W tej sytuacji, jeśli przymocujemy 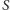 do punktów
do punktów 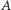 i
i 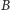 kartki
kartki 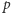 i tak powstałą, sztywną konstrukcję obróćmy o
i tak powstałą, sztywną konstrukcję obróćmy o 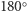 wokół dwusiecznej kąta
wokół dwusiecznej kąta 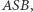 to cień
to cień 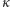 na
na  nie ulegnie zmianie (Rys. 6). Ponieważ cień
nie ulegnie zmianie (Rys. 6). Ponieważ cień  na
na 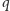 możemy traktować jako cień cienia
możemy traktować jako cień cienia 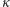 na
na 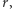 a ten ostatni się nie zmienił, więc koło
a ten ostatni się nie zmienił, więc koło 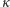 w nowym położeniu również rzuca na
w nowym położeniu również rzuca na 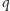 cień w kształcie koła.
cień w kształcie koła.

Rys. 7
Przypuśćmy teraz, że udało się nam wyznaczyć środek okręgu  przy użyciu samej linijki. Poprośmy kolegę z ławki, by zastosował ten sam przepis dla cienia okręgu
przy użyciu samej linijki. Poprośmy kolegę z ławki, by zastosował ten sam przepis dla cienia okręgu  na kartce
na kartce 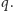 Ze względu na bogate doświadczenie w niesamodzielnej pracy kolega szybko zorientował się, że wystarczy wykonywać "cienie" operacji przeprowadzanych przez nas na okręgu
Ze względu na bogate doświadczenie w niesamodzielnej pracy kolega szybko zorientował się, że wystarczy wykonywać "cienie" operacji przeprowadzanych przez nas na okręgu 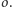 W tej sytuacji uzyskany przez niego kandydat na środek cienia okręgu
W tej sytuacji uzyskany przez niego kandydat na środek cienia okręgu  okaże się cieniem skonstruowanego przez nas środka tego okręgu. Niestety, obaj nie możemy mieć racji, gdyż cień środka odcinka
okaże się cieniem skonstruowanego przez nas środka tego okręgu. Niestety, obaj nie możemy mieć racji, gdyż cień środka odcinka 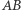 z pewnością nie jest środkiem cienia tego odcinka, do czego powinien przekonać nas rysunek 7. Uzyskana sprzeczność dowodzi, że nie jesteśmy w stanie wyznaczyć środka okręgu, posługując się wyłącznie linijką. Nasze wcześniejsze konstrukcyjne niepowodzenia zostały więc usprawiedliwione - niemożność ma jednak swoje dobre strony.
z pewnością nie jest środkiem cienia tego odcinka, do czego powinien przekonać nas rysunek 7. Uzyskana sprzeczność dowodzi, że nie jesteśmy w stanie wyznaczyć środka okręgu, posługując się wyłącznie linijką. Nasze wcześniejsze konstrukcyjne niepowodzenia zostały więc usprawiedliwione - niemożność ma jednak swoje dobre strony.